From Flat to Hierarchical: Extracting Sparse Representations with Matching Pursuit (2506.03093v1)

Abstract: Motivated by the hypothesis that neural network representations encode abstract, interpretable features as linearly accessible, approximately orthogonal directions, sparse autoencoders (SAEs) have become a popular tool in interpretability. However, recent work has demonstrated phenomenology of model representations that lies outside the scope of this hypothesis, showing signatures of hierarchical, nonlinear, and multi-dimensional features. This raises the question: do SAEs represent features that possess structure at odds with their motivating hypothesis? If not, does avoiding this mismatch help identify said features and gain further insights into neural network representations? To answer these questions, we take a construction-based approach and re-contextualize the popular matching pursuits (MP) algorithm from sparse coding to design MP-SAE -- an SAE that unrolls its encoder into a sequence of residual-guided steps, allowing it to capture hierarchical and nonlinearly accessible features. Comparing this architecture with existing SAEs on a mixture of synthetic and natural data settings, we show: (i) hierarchical concepts induce conditionally orthogonal features, which existing SAEs are unable to faithfully capture, and (ii) the nonlinear encoding step of MP-SAE recovers highly meaningful features, helping us unravel shared structure in the seemingly dichotomous representation spaces of different modalities in a vision-LLM, hence demonstrating the assumption that useful features are solely linearly accessible is insufficient. We also show that the sequential encoder principle of MP-SAE affords an additional benefit of adaptive sparsity at inference time, which may be of independent interest. Overall, we argue our results provide credence to the idea that interpretability should begin with the phenomenology of representations, with methods emerging from assumptions that fit it.

• The paper introduces MP-SAE, which leverages a residual-guided matching pursuit algorithm to iteratively capture hierarchical and multimodal sparse features.
• The MP-SAE architecture outperforms traditional SAEs by achieving higher reconstruction (R²) and Babel scores while preserving feature structure.
• Empirical results demonstrate MP-SAE's adaptive inference-time sparsity and effective extraction of complex, nonlinear representations from both synthetic and pretrained data.

From Flat to Hierarchical: Extracting Sparse Representations with Matching Pursuit

Overview

The paper introduces a novel sparse autoencoder (SAE) architecture, the MP-SAE, which extends the classical Matching Pursuit (MP) algorithm to capture hierarchical, nonlinear, and multimodal features in neural networks. This approach diverges from the Linear Representation Hypothesis (LRH) that enforces globally quasi-orthogonal representations, highlighting limitations of traditional SAEs in capturing conceptual structures like hierarchy and modality-independent features.

Sparse Autoencoders and Linear Representation Hypothesis

SAEs, motivated by the LRH, aim to decompose neural network representations into a set of sparse, approximately orthogonal features. Under LRH, a representation $\bm x$ is decomposed as $\bm x = \bm z\bm D$, where $\bm D$ is an overcomplete dictionary of size $p \gg m$, with quasi-orthogonal columns, and $\bm z$ is a sparse coefficient vector. This setup, which emphasizes linear accessibility of features, has facilitated interpretability in vision and LLMs but fails to accommodate non-linear or hierarchical structures observed in recent empirical studies (Figure 1).

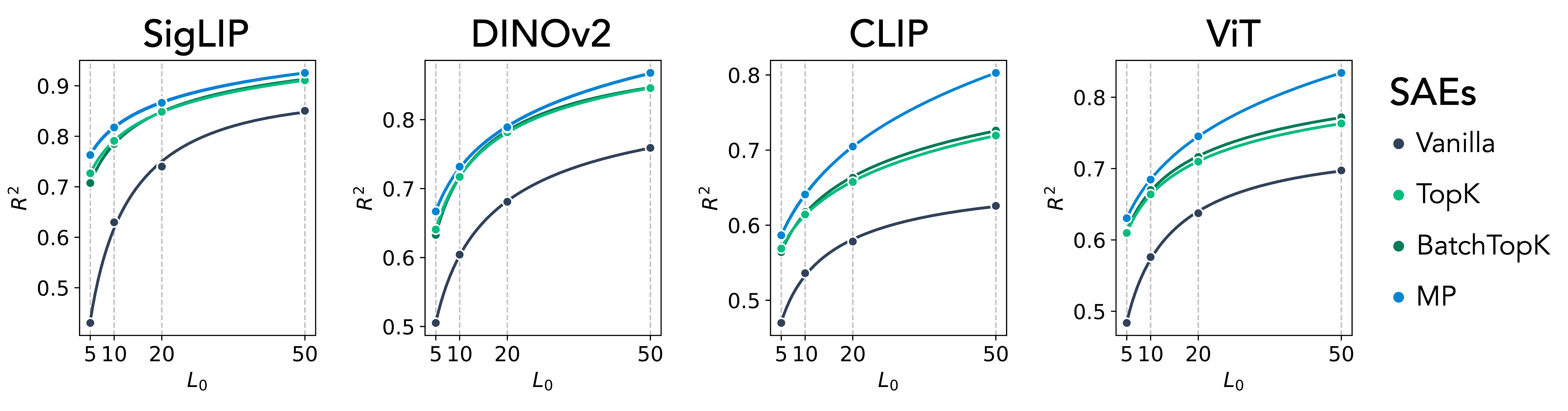
Figure 1: MP-SAE recovers more expressive features than standard SAEs. Reconstruction performance ($R^2$) as a function of sparsity level across four pretrained vision models: SigLIP, DINOv2, CLIP, and ViT. MP-SAE consistently achieves higher $R^2$ at comparable sparsity, indicating more efficient and informative decompositions.

Architectures and Conditional Orthogonality

MP-SAE unrolls its encoder into a sequence of residual-guided steps, promoting conditional orthogonality—orthogonalizing representations only across different hierarchical levels, and thus capturing complex structures beyond LRH's scope. This method iteratively selects features that are orthogonal to what has already been explained, fostering a conditionally orthogonal structure that is naturally hierarchical and multimodally aligned.

Matching Pursuit Sparse Autoencoder (MP-SAE)

MP-SAE's distinctive feature is its ability to sequentially explain input representations through iterative updates, leveraging residual-based greedy selection of features. This process not only fosters conditional orthogonality but also uniquely uncovers higher-order features which are inherently nonlinearly accessible. In this sequential setup, MP-SAE shows consistent performance improvements in capturing both intra- and inter-level feature correlations better than traditional SAEs.

Figure 2: MP-SAE promotes conditional orthogonality at inference. Babel scores for full dictionaries (top) and co-activated subsets (bottom). MP-SAE dictionaries exhibit higher global coherence than standard SAEs, but select more separated features at inference.

Empirical Evaluations

Synthetic Data

MP-SAE outperforms conventional SAEs in synthetic datasets designed to test hierarchical representation capture. It maintains hierarchical structures while also capturing intra-level correlations, a task where traditional architectures fail due to feature absorption.

Pretrained Model Representations

1. Expressivity: MP-SAE achieves higher $R^2$ scores across multiple models, indicating superior feature extraction efficiency.
2. Coherence: Uses Babel score to exhibit its ability to construct coherent but non-interfering feature sets at inference time.
3. Adaptive Inference-Time Sparsity: The monotonically decreasing reconstruction error with an increasing number of active features at inference time distinguishes MP-SAE's flexibility from traditional methods.
4. Multimodal Features: In vision-LLMs, MP-SAE successfully identifies and aligns shared concepts between modalities (Figure 3).

   Figure 3: Distribution of modality scores for features learned by different SAEs, across four vision-LLMs: CLIP, SigLIP, SigLIP2, and AIMv2. In contrast, MP-SAE yields a significantly flatter distribution with substantial density near 0.5, revealing genuinely multimodal features.

Conclusion

The introduction of MP-SAE highlights the architectural enhancements required to interpret complex nonlinear structures in neural representations effectively. Beyond traditional linear assumptions, MP-SAE explores the field of adaptive, dynamically sparse inference, offering theoretical support and practical benefits in recovering richly structured features. The results suggest novel interpretability avenues that more closely reflect the inherent hierarchical and nonlinear nature of learned representations. This work initiates further exploration into enhancing logical coherence and explainability of AI systems, crucial for their deployment in diverse, sensitive domains.