Bound excited states of Fröhlich polarons in one dimension (2506.02440v1)

Abstract: The one-dimensional Fr\"ohlich model describing the motion of a single electron interacting with optical phonons is a paradigmatic model of quantum many-body physics. We predict the existence of an arbitrarily large number of bound excited states in the strong coupling limit and calculate their excitation energies. Numerical simulations of a discretized model demonstrate the complete amelioration of the projector Monte Carlo sign problem by walker annihilation in an infinite Hilbert space. They reveal the threshold for the occurrence of the first bound excited states at a value of $\alpha \approx 1.73$ for the dimensionless coupling constant. This puts the threshold into the regime of intermediate interaction strength. We calculate the spectral weight and the number density of the dressing cloud in the discretized model.

• The paper demonstrates the existence of discrete bound excited states below the phonon continuum at a coupling threshold of α ≈ 1.73.
• The paper employs FCIQMC with the Lee-Low-Pines transformation to overcome the sign problem, accurately computing excitation energies and phonon mode densities.
• The paper’s findings suggest potential experimental detection in narrow quantum wires with implications for advancing electron-phonon interaction research.

Bound Excited States of Fröhlich Polarons in One Dimension

Introduction

Recent advancements have unveiled new insights into the one-dimensional Fröhlich model, capturing the dynamics of an electron within a polarizable medium interacting with optical phonons. The paper elucidates the existence of bound excited states in the strong coupling domain of this model, offering a nuanced perspective on previously undetected phenomena. This model has been foundational in quantum many-body physics, enhancing our understanding of material properties by accurately predicting ground state energies, excitation continuums, and the amelioration of the sign problem through innovative numerical techniques.

The Fröhlich Model

The Fröhlich model, expanded to one dimension, serves as a comprehensive framework for examining electron-phonon interactions. Governed by the Hamiltonian $\hat{H}$, it incorporates various parameters, including the electron momentum ($\hat{p}$), phonon operators ($\hat{a}^\dagger_k$ and $\hat{a}_k$), and a dimensionless coupling constant $\alpha$. The energy spectrum comprises an isolated ground state band and scattering state continuum, with new discrete bound states emerging at intermediate and strong couplings. Notably, excitation energies are analytically derived for large $\alpha$, expanding on classical Pekar functionals and harmonic oscillator analogies.

Numerical Methodology

Full Configuration Interaction Quantum Monte Carlo (FCIQMC) is pivotal in analyzing the polaron system, adeptly sampling ground and excited states without resorting to sign-problem-mitigating approximations. This method leverages walker annihilation mechanics to achieve stochastic error reduction while bypassing typical sign noise constraints. For the Fröhlich model, FCIQMC harnesses the Lee-Low-Pines transformation, allowing efficient numerical computation across various box sizes and coupling strengths, essential for examining bound excited states and phonon mode densities.

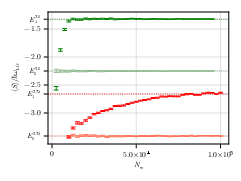
Figure 1: Overcoming the sign problem by walker annihilation. The mean of the shift energy $\langle S\rangle$ is shown as a function of the number of walkers $N_\mathrm{w}$, revealing robustness against the sign problem.

Observations on Bound States

The discovery of bound states below the phonon continuum underscored a threshold at $\alpha \approx 1.73$, indicating practical experimental accessibility. The spectral weights of these states and their energies suggest potential observation through spectroscopic techniques, particularly in systems like narrow quantum wires. The bound states exhibit substantial phonon mode density, diverging from typical ground state characteristics, reflecting deeper electron-phonon coupling at intermediate coupling regimes.

Implications and Future Inquiry

This research suggests a broader applicability of the one-dimensional Fröhlich model to real-world systems, bridging gaps in theoretical predictions and experimental validations. The implications extend to applications in material science and condensed matter physics, offering potential pathways to exploit polaronic interactions for electronic and photonic advancements. Future exploration could encompass scaling FCIQMC methodologies to higher-dimensional models, deepening the exploration of bound states' roles in quantum systems.

Conclusion

The identification of bound excited states in the one-dimensional Fröhlich model marks a significant pivot in understanding electron-phonon interactions under strong coupling scenarios. The paper reaffirms the utility of FCIQMC as a formidable tool in quantum calculations, enhancing the precision of computational techniques without succumbing to traditional limitations. Continued advancements in these methodologies promise further breakthroughs in the quantum many-body domain, with promising applications in experimental and theoretical research landscapes.