$XX^{t}$ Can Be Faster (2505.09814v2)

Abstract: We present RXTX, a new algorithm for computing the product of matrix by its transpose $XX^{t}$ for $X\in \mathbb{R}^{n\times m}$. RXTX uses $5\%$ fewer multiplications and $5\%$ fewer operations (additions and multiplications) than State-of-the-Art algorithms. Note that the accelerations not only holds asymptotically for large matrices with $n \rightarrow \infty$, but also for small matrices including $n = 4$. The algorithm was discovered by combining Machine Learning-based search methods with Combinatorial Optimization.

• The paper presents the RXTX algorithm that reduces computational complexity for calculating XXᵗ by decreasing multiplications and additions.
• It leverages recursive block matrix multiplication and AI-guided strategies to achieve a consistent 9% runtime speedup over traditional BLAS routines.
• Empirical results validate RXTX's efficiency, outperforming previous state-of-the-art methods in 99% of test cases and large dense matrix simulations.

Computation of $XX^{t}$ Using RXTX Algorithm

The RXTX algorithm represents a novel approach to computing the product of a matrix with its transpose, referred to as $XX^{t}$. This essay provides an in-depth analysis of the RXTX algorithm presented in the paper "XX^{t} Can Be Faster" (2505.09814), exploring how it achieves improvements over existing methods for this type of matrix multiplication.

Introduction to RXTX Algorithm

RXTX emerges as an AI-designed algorithm for calculating the matrix-by-transpose product, $XX^{t}$, with notable efficiency gains. By leveraging AI-driven search combined with combinatorial optimization, RXTX reduces the computational burden by approximately 5% when compared to previous state-of-the-art (SotA) methods. This reduction is achieved by using 5% fewer multiplications and additions even for relatively small matrix sizes.

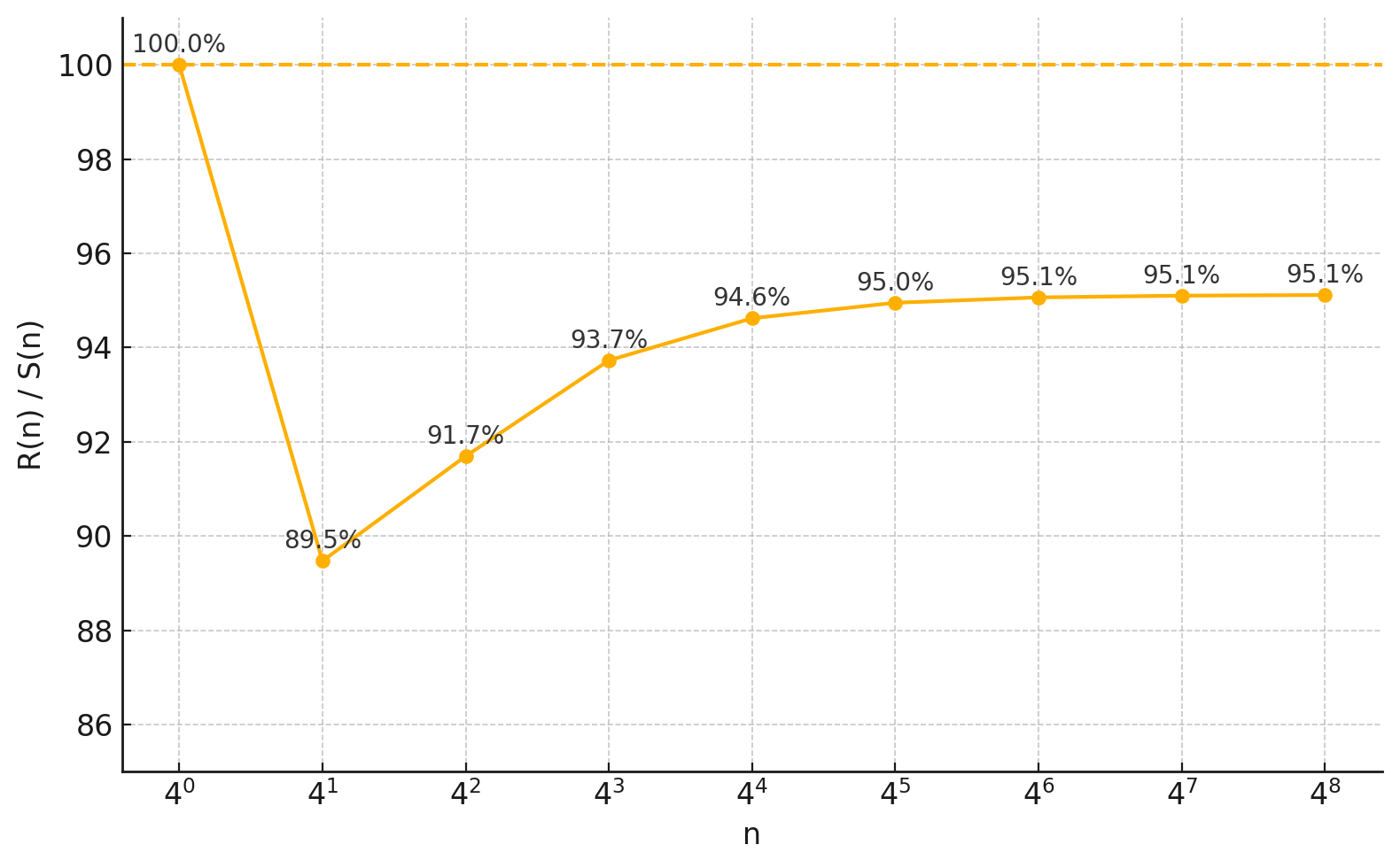
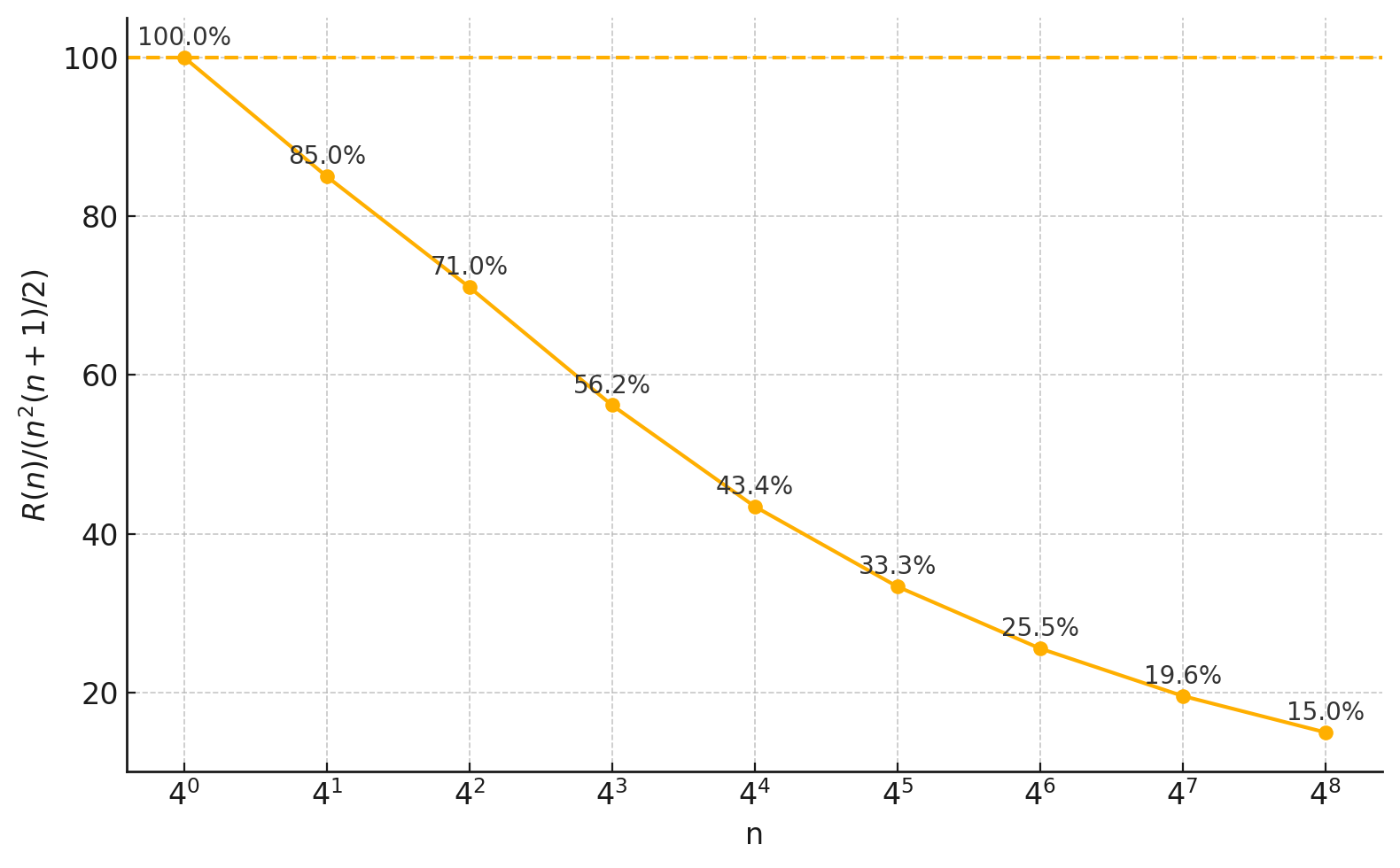
Figure 1: Comparison of number of multiplications of RXTX to previous SotA and naive algorithm.

Computational Core of RXTX

RXTX's architecture capitalizes on recursive block matrix multiplication. When breaking down the recursion and multiplications for matrices sized $n \times n$, RXTX reduces the necessary multiplications and additions through optimized recursive calls:

• Recursive Calls: RXTX uses 8 recursive calls juxtaposed against 4 for recursive Strassen, while maintaining a reduction in multiplications.
• General Products: It integrates 26 general matrix multiplications, optimizing the calculation for $4 \times 4$ block matrices as opposed to traditional 16 recursive calls in previous algorithms.

The formal recursive formulas for the number of multiplications and operations highlight RXTX's efficiency over recursive Strassen and naive algorithms. For large matrix sizes, these reductions manifest as concrete runtime benefits seen in practical implementations.

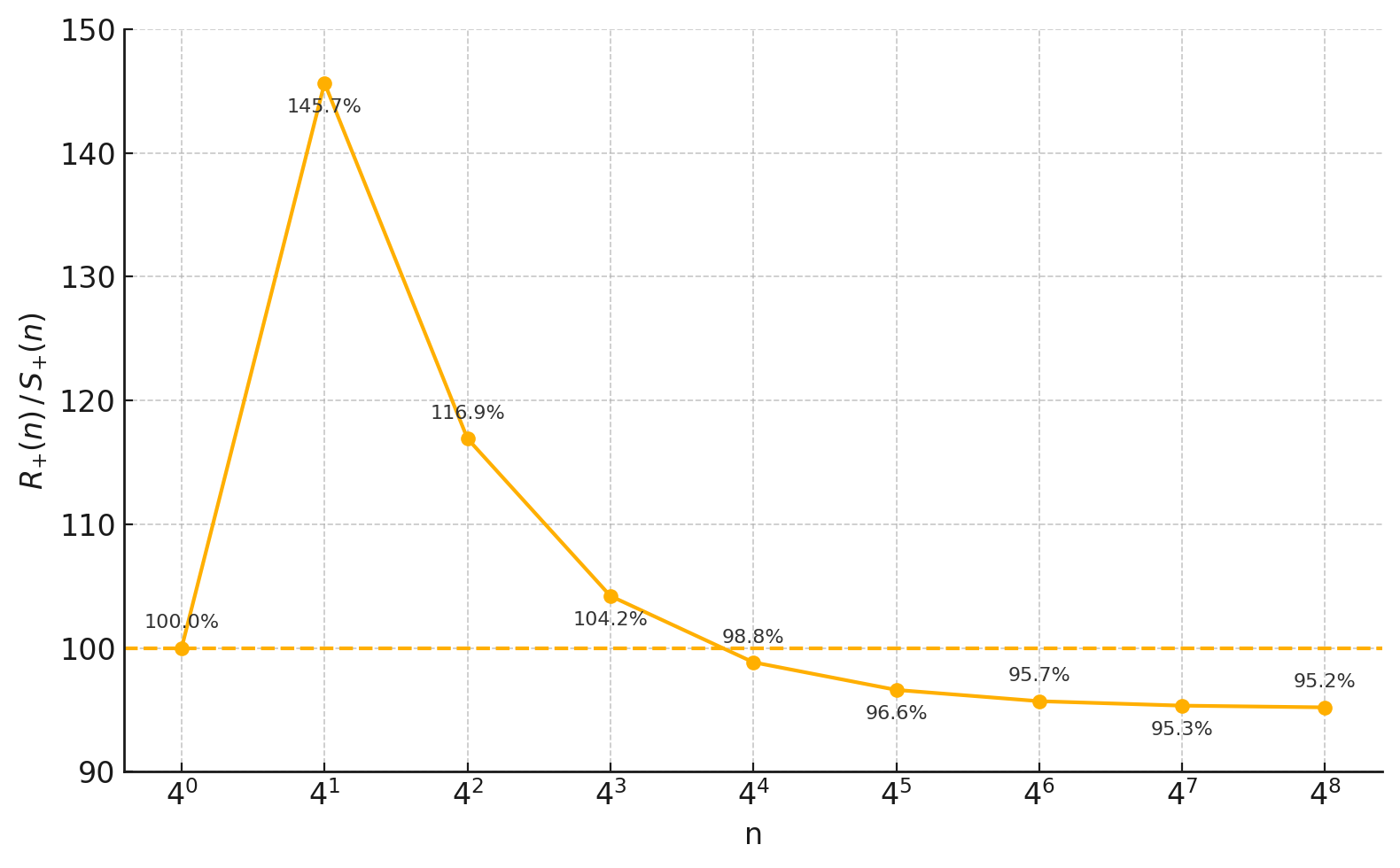
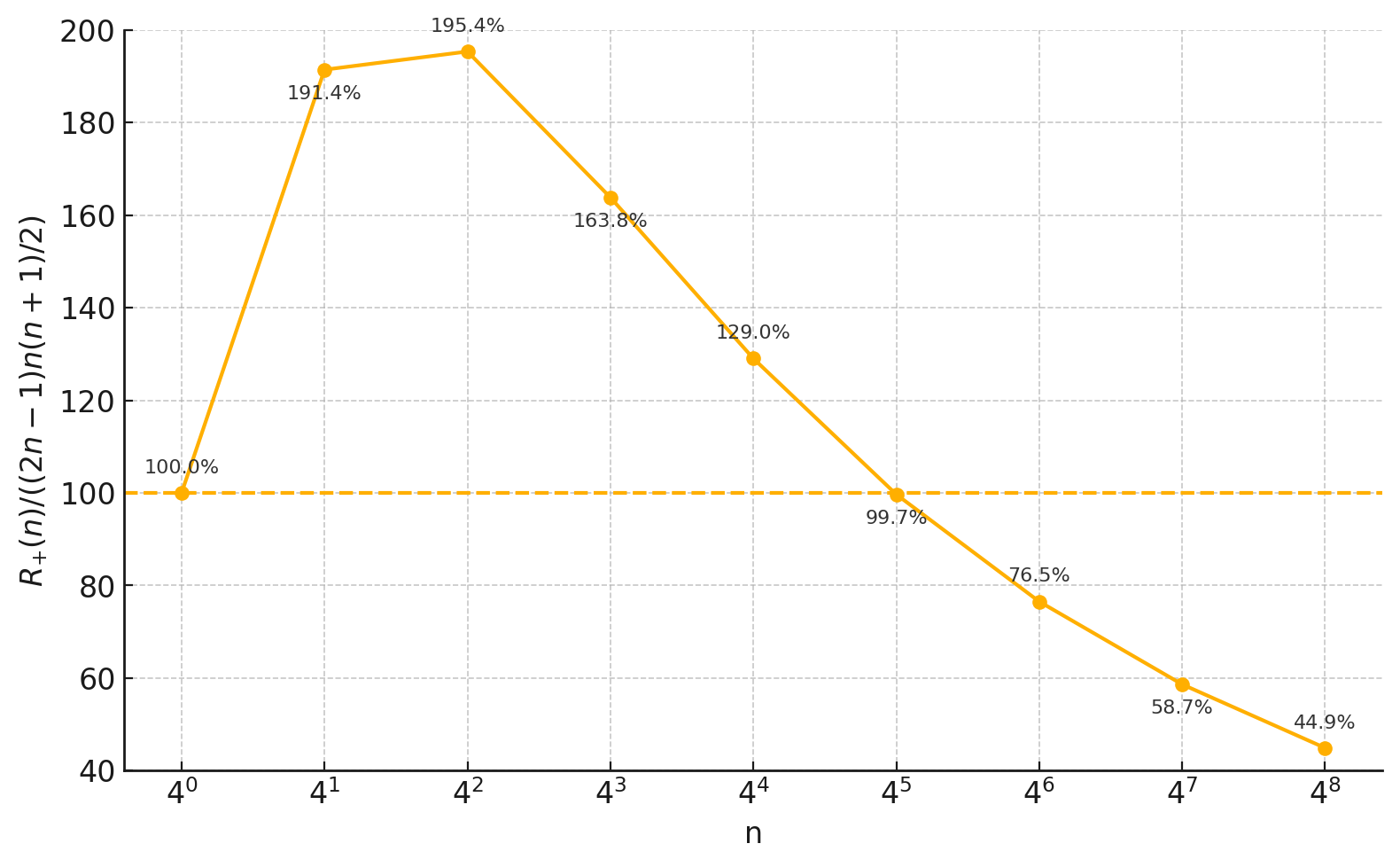
Figure 2: Comparison of number of operations of RXTX to recursive Strassen and naive algorithm. RXTX outperforms recursive Strassen for $n \geq 256$ and naive algorithm for $n \geq 1024.</p></p> <h2 class='paper-heading' id='performance-and-efficiency-gains'>Performance and Efficiency Gains</h2> <p>RXTX&#39;s real-world performance was validated through a series of computational experiments simulating large dense matrices with random normal entries. These tests demonstrated RXTX&#39;s capability to outperform traditional matrix multiplication routines available in standard linear algebra libraries like BLAS:</p> <ul> <li><strong>Speedup</strong>: Empirical results suggest an average runtime acceleration of 9% for RXTX, outperforming the reference BLAS routines used for direct $XX^{t}$$computation.</li> <li><strong>Consistency</strong>: RXTX was faster in 99<img src="https://emergentmind-storage-cdn-c7atfsgud9cecchk.z01.azurefd.net/paper-images/2505-09814/rxtx_25_09.png" alt="Figure 3" title="" class="markdown-image" loading="lazy"> <p class="figure-caption">Figure 3: The average runtime for RXTX is 2.524s, which is 9</ul> <h2 class='paper-heading' id='discovery-methodology'>Discovery Methodology</h2> <p>RXTX was discovered using a sophisticated RL-guided Large Neighborhood Search (LNS), augmented by Mixed Integer Linear Programming (MILP) strategies:</p> <ul> <li><strong>RL-guided LNS</strong>: Utilizing <a href="https://www.emergentmind.com/topics/reinforcement-learning-rl" title="" rel="nofollow" data-turbo="false" class="assistant-link" x-data x-tooltip.raw="">reinforcement learning</a> agents to propose rank-1 bilinear product sets. These candidate sets are refined through MILP-based exhaustive enumeration to identify compact combinations achieving the target expressions.</li> <li><strong>MILP Pipeline</strong>: Two-tier MILP optimizes the subset selection ensuring comprehensive coverage of$$XX^{t}$$target expressions, streamlining the algorithm to its most efficient form.</li> </ul> <p>This approach parallels simplified strategies of the AlphaTensor RL framework but is uniquely tailored to target tensor products for structured matrix operations.</p> <h2 class='paper-heading' id='conclusion'>Conclusion</h2> <p>The RXTX algorithm embodies a significant advancement in efficient matrix multiplication, particularly for computations involving$$XX^{t}$. Its AI-assisted discovery process and the subsequent computational gains underscore the pivotal role of modern algorithms in enhancing linear algebra operations. The indicating performance metrics set a new benchmark within the domain, inviting further exploration and potential extension of RXTX to other structured matrix scenarios.