TriADA: Massively Parallel Trilinear Matrix-by-Tensor Multiply-Add Algorithm and Device Architecture for the Acceleration of 3D Discrete Transformations (2506.22818v1)

Abstract: Multilinear transformations are key in high-performance computing (HPC) and AI workloads, where data is represented as tensors. However, their high computational and memory demands, which grow with dimensionality, often slow down critical tasks. Moreover, scaling computation by enlarging the number of parallel processing units substantially increases energy consumption, limiting widespread adoption, especially for sparse data, which is common in HPC and AI applications. This paper introduces the Trilinear Algorithm and isomorphic to algorithm Device Architecture (TriADA) to address these challenges with the following innovations: (1) a massively parallel, low-rank algorithm for computing a family of trilinear (3D) discrete orthogonal transformations (3D-DXTs), which is a special case of the more general 3-mode matrix-by-tensor multiplication (3D-GEMT); (2) a new outer-product-based GEMM kernel with decoupled streaming active memory, specially designed to accelerate 3D-GEMT operation; (3) an isomorphic to the proposed algorithm, fully distributed 3D network of mesh interconnected processing elements or cells with a coordinate-free, data-driven local processing activity, which is independent of problem size; (4) an elastic sparse outer-product (ESOP) method that avoids unnecessary computing and communication operations with zero-valued operands, thereby enhancing energy efficiency, computational accuracy, and stability. TriADA is capable of performing a variety of trilinear transformations with hypercubic arithmetic complexity in a linear number of time-steps. The massively parallel, scalable, and energy-efficient architecture of TriADA is ideal for accelerating multilinear tensor operations, which are the most demanding parts of AI and HPC workloads.

• The paper introduces a novel trilinear matrix-by-tensor multiply-add algorithm that significantly enhances computational efficiency for 3D discrete transformations.
• It outlines a unified 3D network architecture with three processing stages that optimizes tensor partitioning and data movement for improved performance.
• The approach integrates an Elastic Sparse Outer-product Processing method to manage data sparsity, reducing redundant computations and conserving energy.

TriADA: Massively Parallel Trilinear Matrix-by-Tensor Multiply-Add Algorithm and Device Architecture for 3D Discrete Transformations

Introduction

The paper presents the TriADA approach, which encompasses both a trilinear algorithm and its isomorphic device architecture. These innovations aim to enhance the computation of multilinear transformations—specifically focusing on trilinear (3D) discrete orthogonal transformations—critical for HPC and AI workloads.

Multilinear transformations, particularly those using tensors, are essential in computational fields such as signal processing and AI. However, these operations face challenges in computational and memory demands that scale non-linearly with dimensionality. TriADA addresses these challenges by introducing a massively parallel low-rank algorithm for efficient computation of trilinear transformations mapped onto a unified 3D network of processing elements, interconnected by mesh networks, thereby supporting both computational acceleration and energy efficiency.

Trilinear Orthogonal Transforms

Basic Equations

The essence of the trilinear orthogonal transformation, expressed as both forward and inverse operations, is grounded in matrix-by-tensor multiplication. This computation changes the coordinates of a 3D data tensor using orthogonal matrices. The algorithm described transforms the data coordinates efficiently through a structured sequence of summations detailed in the equations.

Types and Complexity

Several types of trilinear orthogonal transformations (e.g., DFT, DCT, DWHT) rely on specific coefficient matrices that may be symmetric, orthogonal, or unitary. Each type has inherent mathematical properties offering different computational benefits, which are described using the appropriate mathematical constructs. Notably, these transformations can achieve highly efficient computation expressed in the form of matrix-by-tensor multiplications, without necessitating data to be organized in a square shape or restricted to power-of-two sizes.

Tensor Partition and GEMT Multiplication

Partition Schemes

The multidimensional tensor can be partitioned along different planes to facilitate GEMT computations. This partitioning reduces computational complexity by decreasing the dimensionality of the iteration space, transforming what would otherwise be a monolithic 6D space into multiple manageable 4D spaces.

Outer-product Notation

Transformations can be processed using dot-product notation or more efficiently via outer-product notation, which aggregates operations and allows for a linear number of time steps in computation—key to efficient tensor transformations in TriADA.

Mapping Algorithm's Index Space to Processor Space

Linear Mapping

The spatial mapping technique, crucial for reducing computational complexity, enables mapping from a higher-dimensional algorithm space to a lower-dimensional processing space, ensuring structured overlapping and data reuse through strategic time-step assignments. This methodology ensures processing within TriADA accommodates different index spaces of the algorithm without conflict.

Acceleration of Trilinear Discrete Transforms

New Kernel Design

TriADA introduces a unique kernel tailored for outer-product-based processing, capable of efficiently handling square-by-rectangular matrix multiplications crucial for transforming both tensor and matrix data stored within its tensor core network.

Stage-based Acceleration

Stage I

The initial stage performs rank-1 updates using outer-product arithmetic, leveraging diagonal tagging to independently activate cells for computation, driven entirely by the input data.

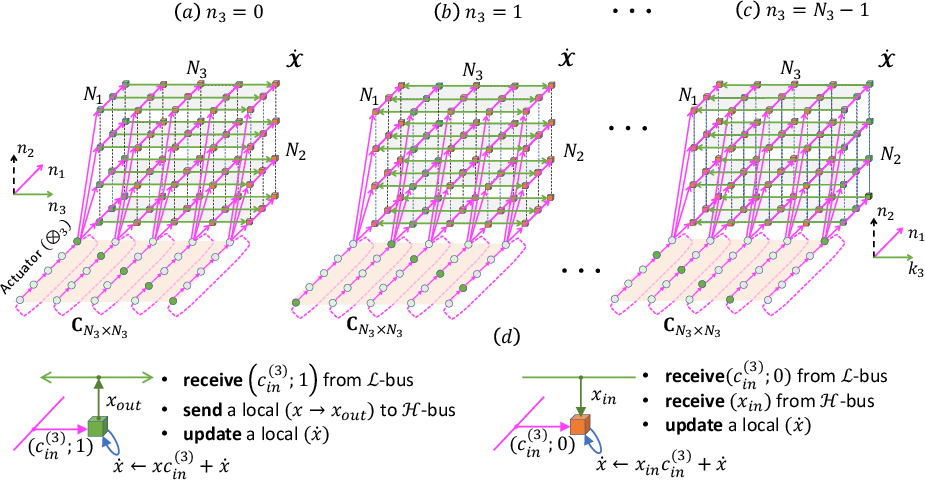
Figure 1: Stage I: computing and data movement on each time-step $n_3\in[0,N_3)$, where $c_{in}^{(3)}$ is a corresponding element.

Stage II

In the second stage, the dimensionality shifts to focus on row-based data streaming and matrix updates accomplished through lateral data movement.

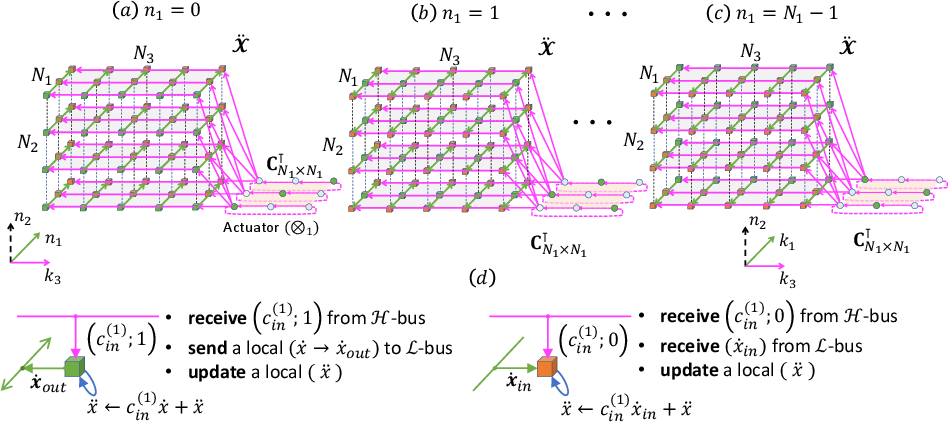
Figure 2: Stage II: computing and data movement on each of $N_1$ time-steps.

Stage III

The final stage completes the trilinear transformation with frontal streaming of residual data, achieving full tensor transformation through sequential yet parallel operations.

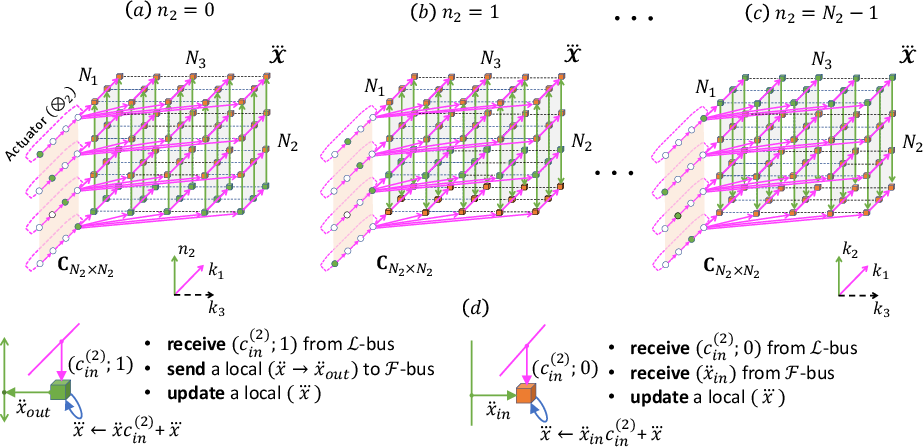
Figure 3: Stage III: computing and data movement on each of $N_2$ steps.

Management of Unstructured Data Sparsity

ESOP Method

The Elastic Sparse Outer-product Processing (ESOP) method enhances performance by efficiently handling sparse data, minimizing computational and communication redundancies. It employs a mechanism that dynamically adapts to sparse vectors, optimizing update frequencies and conserving energy.

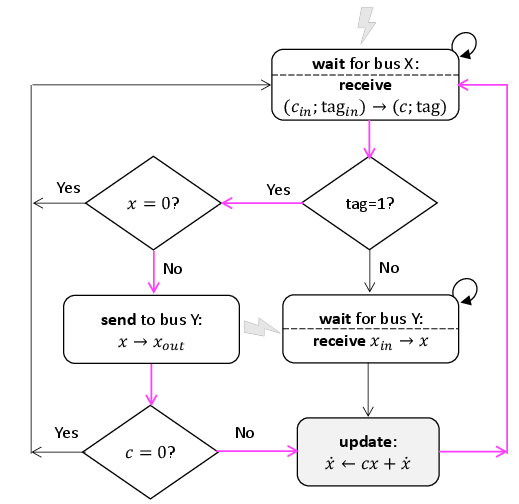
Figure 4: Diagram of cell's activity to manage data sparsity.

Conclusion

TriADA's unique blend of algorithmic and architectural innovations positions it as a tool to fundamentally enhance tensor transformation capabilities for AI and HPC workloads, balancing energy efficiency with computational power. Through its scalable approach, TriADA anticipates future computing demands within high-performance sectors, enabling significant advancements in tensor operation efficiency.

The implications of TriADA touch on various domains, specifically where tensor operations are central, contributing to ongoing developments in AI and HPC infrastructure. Future work might explore further optimizing operations for emerging transistor technologies or adapting the architecture to newer application-specific processors.