Inverse Problem Sampling in Latent Space Using Sequential Monte Carlo (2502.05908v3)

Abstract: In image processing, solving inverse problems is the task of finding plausible reconstructions of an image that was corrupted by some (usually known) degradation operator. Commonly, this process is done using a generative image model that can guide the reconstruction towards solutions that appear natural. The success of diffusion models over the last few years has made them a leading candidate for this task. However, the sequential nature of diffusion models makes this conditional sampling process challenging. Furthermore, since diffusion models are often defined in the latent space of an autoencoder, the encoder-decoder transformations introduce additional difficulties. To address these challenges, we suggest a novel sampling method based on sequential Monte Carlo (SMC) in the latent space of diffusion models. We name our method LD-SMC. We define a generative model for the data using additional auxiliary observations and perform posterior inference with SMC sampling based on a reverse diffusion process. Empirical evaluations on ImageNet and FFHQ show the benefits of LD-SMC over competing methods in various inverse problem tasks and especially in challenging inpainting tasks.

• The paper introduces LD-SMC, integrating auxiliary observations in latent space with SMC sampling for effective image inpainting and reconstruction.
• It employs a novel Gibbs sampling and reverse diffusion approach, outperforming baselines in perceptual quality on datasets like ImageNet.
• Empirical results demonstrate competitive performance in Gaussian deblurring and super-resolution, offering robust solutions for inverse problems.

Inverse Problem Sampling in Latent Space Using Sequential Monte Carlo

Introduction

The paper "Inverse Problem Sampling in Latent Space Using Sequential Monte Carlo" (LD-SMC) addresses the challenge of solving inverse problems in image processing by employing a novel approach that leverages sequential Monte Carlo (SMC) methods within the latent space of diffusion models. Diffusion models have shown significant promise in this domain due to their generative capabilities and their ability to model complex image priors. However, the sequential nature of these models, especially when integrated with the transformations of autoencoders, complicates their application to conditional sampling tasks required by inverse problems.

LD-SMC proposes a solution by incorporating auxiliary observations into the latent space and performing posterior inference through SMC sampling based on a reverse diffusion process. This method is designed to handle inverse problems more effectively, especially challenging tasks like image inpainting, where the goal is to restore parts of an image that have been corrupted or missing.

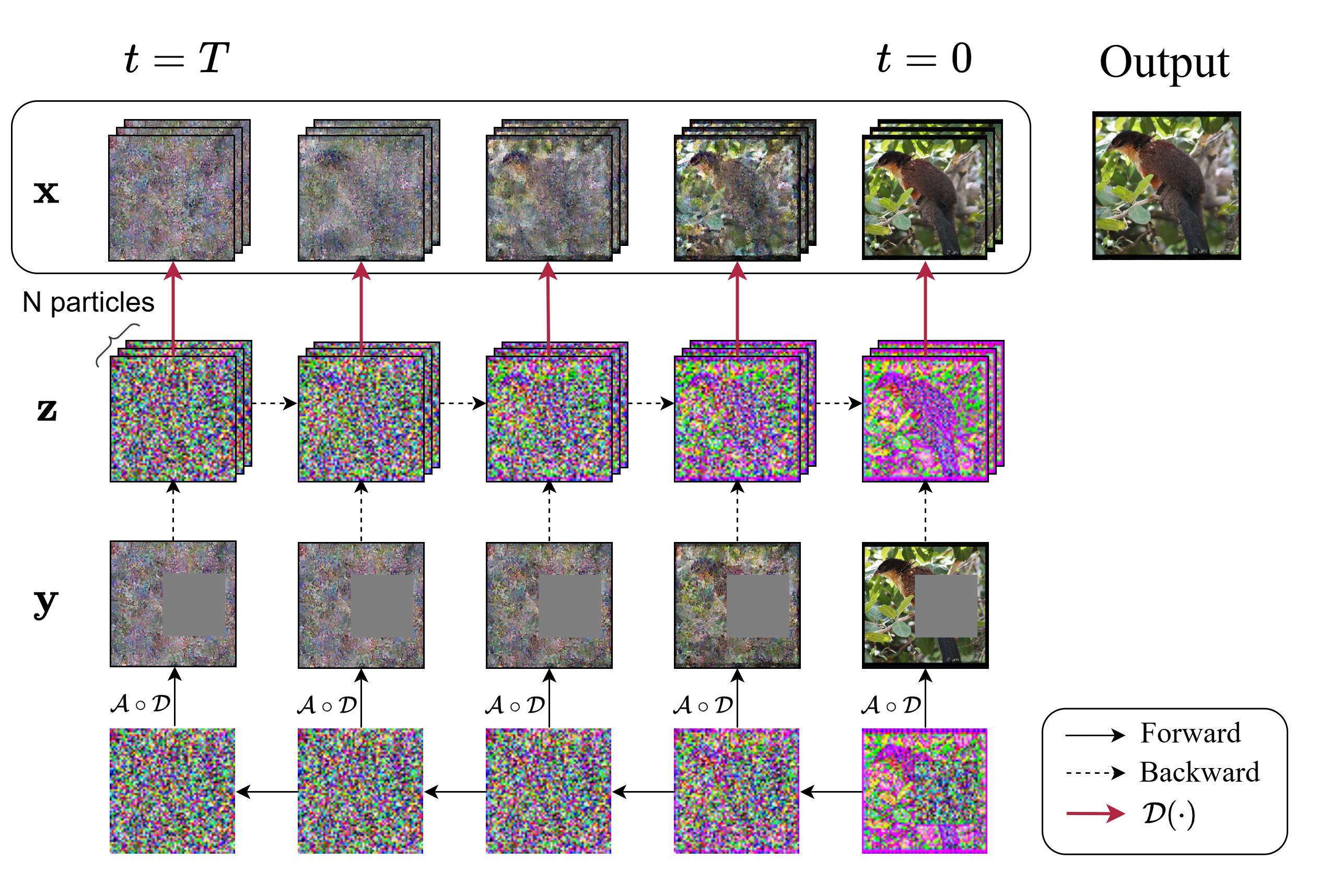
Figure 1: LD-SMC solves inverse problem tasks in the latent space of autoencoders by utilizing auxiliary observations $_{1:T}$ initialized using the DDIM forward process.

Methodology

The LD-SMC method is built upon several core elements:

1. Generative Model: A generative model is defined in the latent space of autoencoders. Here, auxiliary observations are utilized to inform the sampling process. This model uses the reverse diffusion process to perform posterior inference on latent variables efficiently.
2. Sequential Monte Carlo (SMC): SMC is employed to sample from the posterior distribution. The algorithm begins with a set of particles sampled from the prior distribution and iterates through the latent space using carefully designed proposal distributions and weighting schemes. The proposal distributions are constructed to align with the diffusion model's prior mean while correcting based on observed auxiliary information and the corrupted image data.
3. Auxiliary Observations: The use of auxiliary observations ($_{1:T}$) allows the model to capture finer detail by incorporating evidence from future steps in the diffusion process. This integration helps mitigate the challenges of sampling from non-linear corruption models inherent in Latent Diffusion Models (LDMs).
4. Gibbs Sampling: The paper outlines an iterative Gibbs sampling approach that combines the generative model and SMC to refine the results progressively. The procedure alternates between sampling auxiliary observations and latent variables, anchoring the process in both local semantics and global image structures.

   Figure 2: Comparison between LD-SMC and baseline methods on inpainting of ImageNet images.

Results

The empirical evaluations show that LD-SMC outperforms several baseline methods across multiple inverse problem tasks. The experiments, conducted on datasets such as ImageNet and FFHQ, demonstrate the ability of LD-SMC to generate high-quality reconstructions, particularly in tasks involving inpainting and super-resolution.

• Inpainting: LD-SMC exhibits significant improvements in perceptual quality compared to other methods, providing more natural and coherent completions of missing image regions, especially noticeable in diverse datasets like ImageNet.
• Gaussian Deblurring and Super-resolution: The method demonstrates competitive performance, maintaining high fidelity and perceptual quality in reconstructed images.

  Figure 3: Comparison between LD-SMC and baseline methods on Gaussian deblurring of ImageNet images.

Implications and Future Work

The introduction of auxiliary observations in the latent space, combined with SMC, opens new avenues for solving complex inverse problems in image processing. The approach addresses key limitations of existing methods that rely heavily on linear models, offering a more robust framework adaptable to non-linear settings.

Potential future developments include optimizing computational efficiency, exploring adaptive particle scaling strategies, and extending the methodology to other domains such as video processing or 3D image reconstruction. Moreover, further refinement of the proposal distributions and the integration of advanced hyperparameter tuning could enhance performance even further.

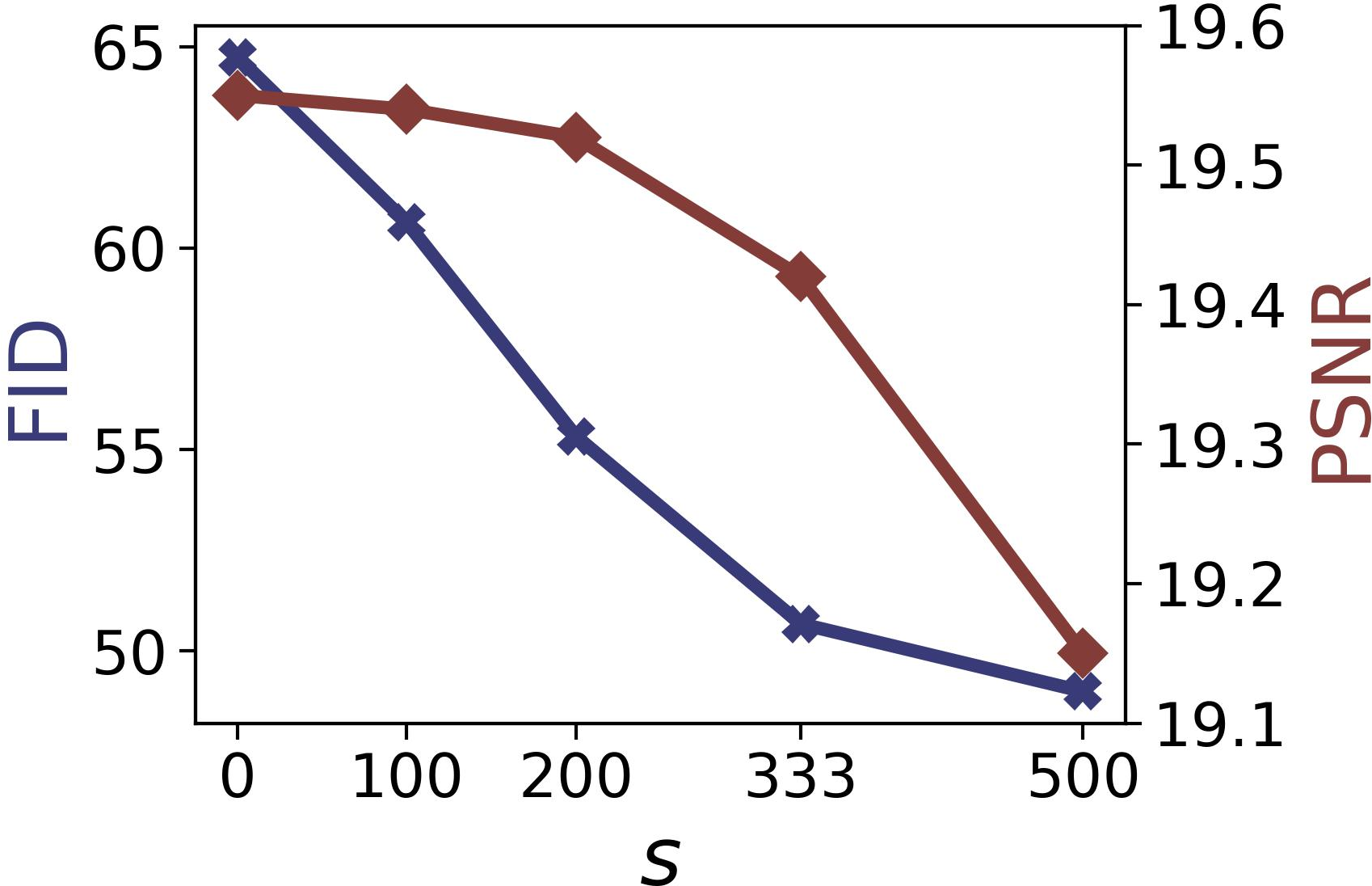
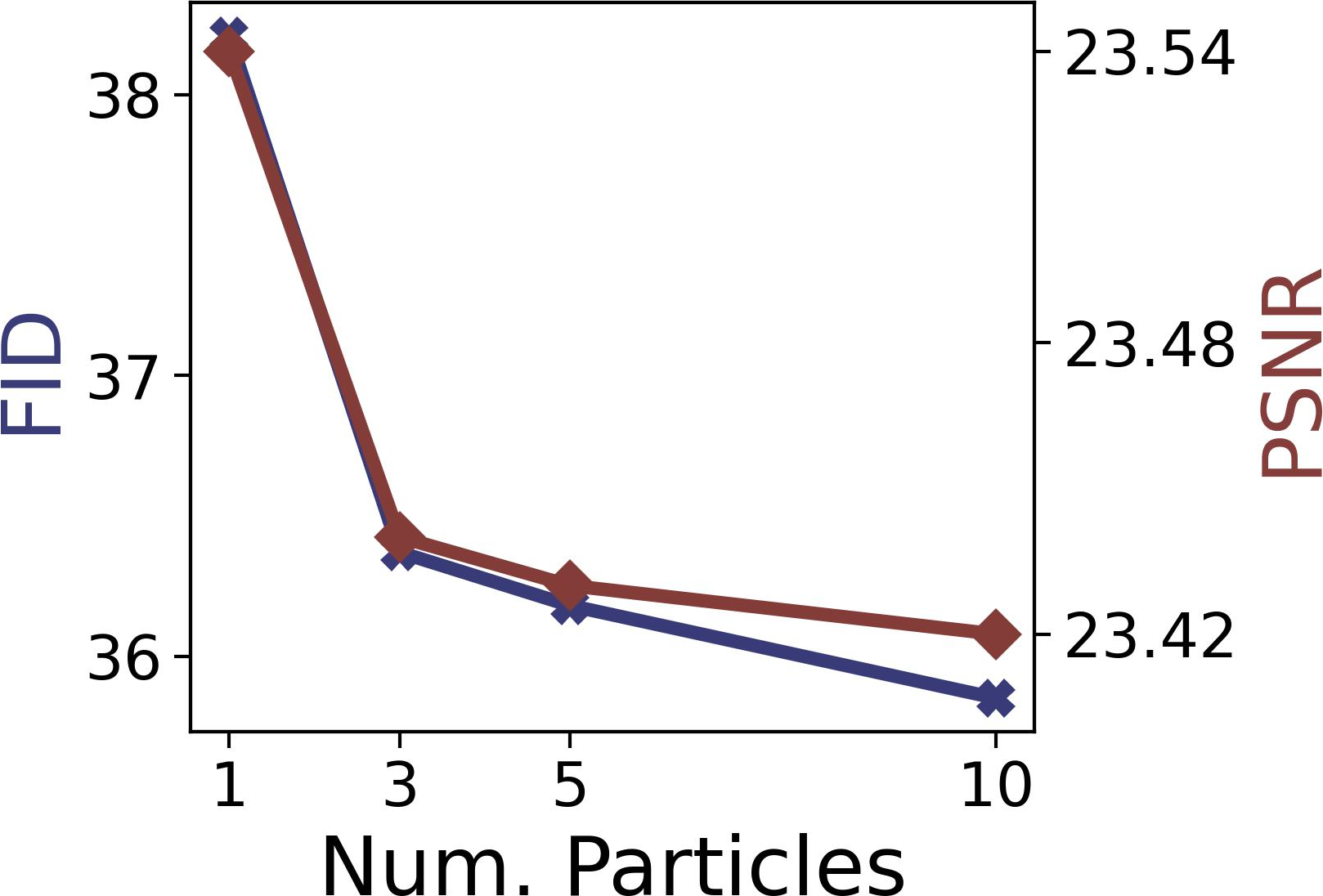
Figure 4: FID and PSNR values when varying s (left) and the number of particles N (right) on ImageNet box (left) and free-form (right) inpainting tasks.

Conclusion

LD-SMC introduces a powerful method for addressing the challenges of inverse problems by leveraging latent space diffusion models with sequential Monte Carlo sampling. Its integration of auxiliary observations and novel sampling procedures provides a strong foundation for high-quality image reconstruction tasks, demonstrating its efficacy across various problem sets and datasets. The research paves the way for further innovations in utilizing diffusion models for complex generative tasks while maintaining computational feasibility and robustness.