Virtual Sensing to Enable Real-Time Monitoring of Inaccessible Locations \& Unmeasurable Parameters (2412.00107v1)

Abstract: Real-time monitoring of critical parameters is essential for energy systems' safe and efficient operation. However, traditional sensors often fail and degrade in harsh environments where physical sensors cannot be placed (inaccessible locations). In addition, there are important parameters that cannot be directly measured by sensors. We need ML-based real-time monitoring in those remote locations to ensure system operations. However, traditional ML models struggle to process continuous sensor profile data to fit model requirements, leading to the loss of spatial relationships. Another challenge for real-time monitoring is ``dataset shift" and the need for frequent retraining under varying conditions, where extensive retraining prohibits real-time inference. To resolve these challenges, this study addressed the limitations of real-time monitoring methods by enabling monitoring in locations where physical sensors are impractical to deploy. Our proposed approach, utilizing Multi-Input Operator Network virtual sensors, leverages deep learning to seamlessly integrate diverse data sources and accurately predict key parameters in real-time without the need for additional physical sensors. The approach's effectiveness is demonstrated through thermal-hydraulic monitoring in a nuclear reactor subchannel, achieving remarkable accuracy.

• The paper introduces MIONet, a novel Multi-Input Operator Network that integrates diverse sensor inputs to predict critical thermal-hydraulic parameters.
• The model achieves high accuracy with relative L2 errors of 0.2%, 0.8%, and 1.4% for temperature, velocity, and turbulence kinetic energy respectively, outperforming conventional CFD simulations.
• The approach enables real-time inference, reducing computation time from ~587 seconds in CFD simulations to approximately 5.24×10⁻³ seconds, facilitating monitoring in inaccessible reactor subchannels.

MIONet for Virtual Sensing in Inaccessible Environments

This paper introduces a Multi-Input Operator Network (MIONet) for virtual sensing, enabling real-time monitoring of critical parameters in inaccessible locations and predicting unmeasurable quantities. The approach leverages deep learning to integrate diverse data sources and accurately predict key parameters in real-time, demonstrated through thermal-hydraulic monitoring in a nuclear reactor subchannel.

Background and Motivation

Virtual sensors are essential for energy systems' safe and efficient operation, especially in harsh environments where physical sensors are impractical or when parameters cannot be directly measured. Traditional ML models struggle with continuous sensor data, losing spatial relationships, and dataset shift necessitates frequent retraining, hindering real-time inference. DeepONets can address these limitations by learning mappings between function spaces but are limited in handling multiple simultaneous inputs. The paper addresses these challenges using a MIONet architecture [jin2022mionet] to develop advanced virtual sensors for real-time monitoring of key parameters in inaccessible locations.

Methods and Implementation

The paper focuses on developing a real-time monitoring model for thermal-hydraulic conditions within nuclear reactor subchannels. The goal is to develop a surrogate model capable of predicting specific thermal-hydraulic parameters at the center of the subchannel, using coolant inlet conditions and the reactor's heat generation profile as inputs. This model must be computationally lightweight for real-time application and adaptable to diverse operating conditions.

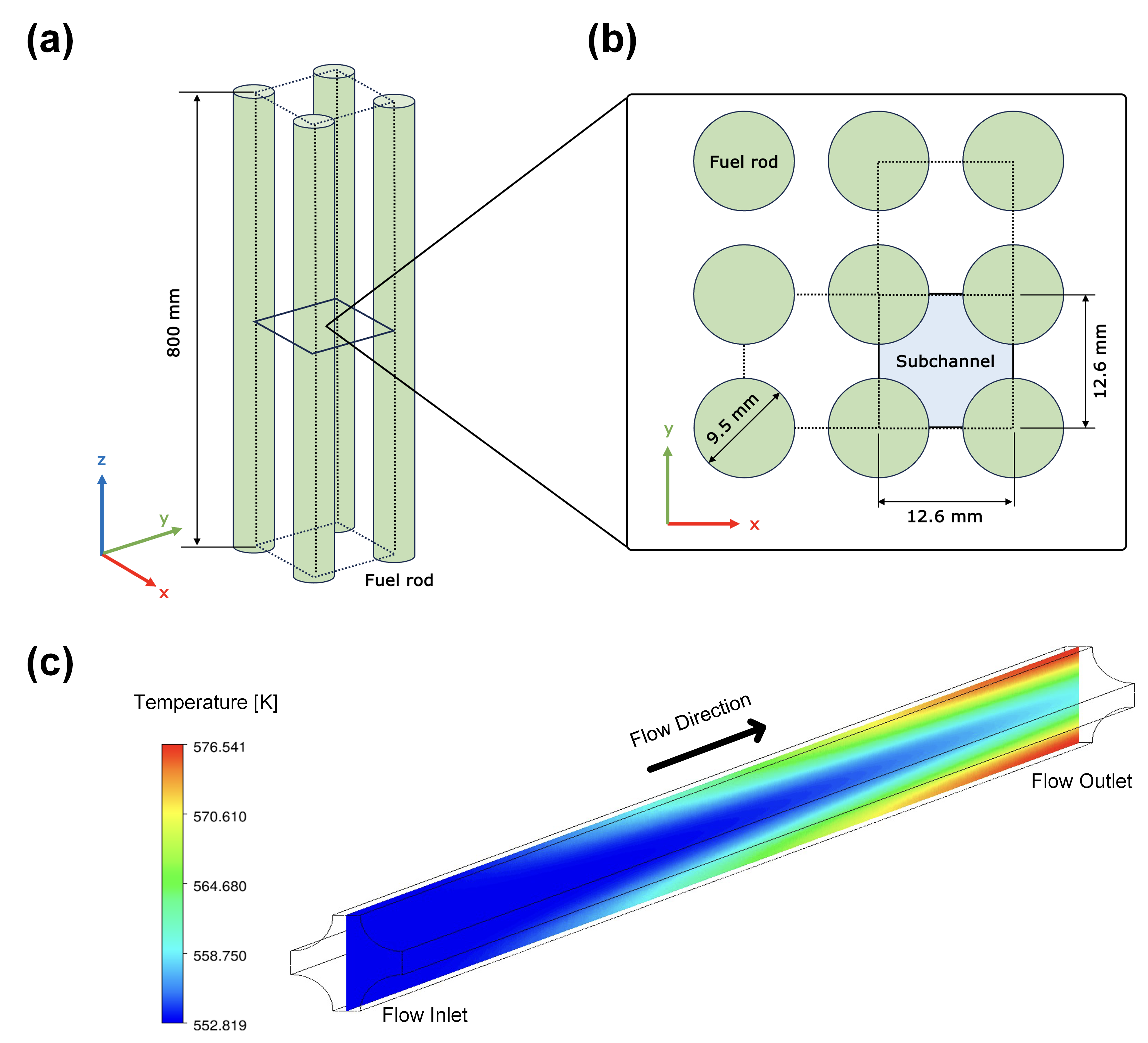
Figure 1: (a): Perspective view of a nuclear fuel assembly illustrating the arrangement of fuel rods (green cylinders) and their vertical alignment. (b): Cross-sectional view at the fuel assembly's center plane, detailing the fuel rods' geometric layout and the subchannel (blue region) where coolant flows. (c) Typical temperature distribution inside the PWR subchannel. Direct measurement within these subchannels is challenging due to geometric constraints and the potential disruption caused by installing traditional sensors such as flowmeters or thermocouples, which could affect the reactor core's design and operation.

Data Generation

The simulation focuses on a square subchannel extracted from a fuel rod array. Tetrahedral meshes were employed to discretize the computational domain (Figure 2). A Reynolds-Averaged Navier-Stokes (RANS) simulation with the RNG $k-\epsilon$ turbulence model was chosen for computational efficiency.

Figure 2: Grid Generation over the Computational Domain, which illustrates the careful resolution of the boundary layer near the fuel rod walls.

The inlet velocity magnitude $(v_{in})$ and temperature $(T_{in})$ were varied, and a sinusoidal heat flux ($P_{max}$) was applied to the fuel rod surfaces. ANSYS Fluent was employed to solve fluid flow and heat transfer governing equations.

MIONet Architecture

The MIONet architecture comprises multiple branch networks for encoding input functions ($P_{rod}$, $T_{in}$, and $v_{in}$) and a single trunk network for encoding the domain of the output function ($pos$), illustrated in Figure 3. The low-rank version of MIONet employs element-wise multiplication to combine outputs from the branch networks with the trunk network. The final output of MIONet, aggregated over all points in the output space, is obtained by element-wise multiplication of the trunk network output tensor $\psi$ with the combined outputs of the branch networks. This product is summed across all points $y \in Y$, and a bias term $b$ is added.

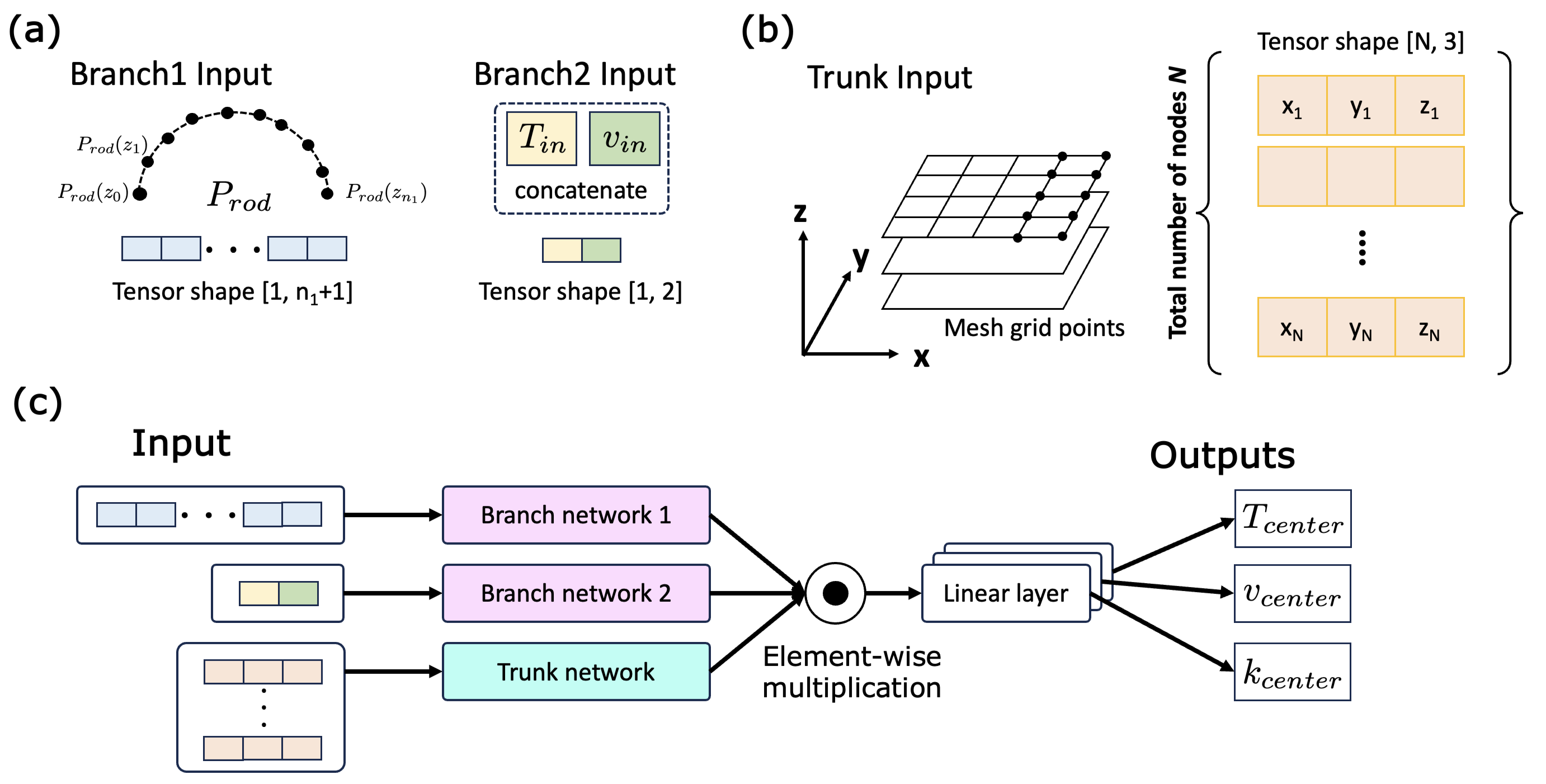
Figure 3: (a) Description of branch inputs; $P_{rod}$ represents a functionally discretized input at fixed sensor locations, while $T_{in}$ and $v_{in}$ are treated as constant variables. (b) Representation of the output domain: it illustrates the node positions at the center of a subchannel, as specified in a computational mesh.(c) Architecture of the Multi-input Operator Network. Branch networks are utilized to encode $P_{rod}$ along the nuclear fuel rod, $T_{in}$, and $v_{in}$. The trunk network encodes the spatial domain of the outputs. The output quantities are distributions of $T_{center}$, $v_{center}$ and $k_{center}$.

Each branch network comprises three hidden layers [512, 512, 512], incorporating ReLU activations and dropout layers with a rate of 0.2. The trunk network projects a two-dimensional vector through hidden layers [300, 300, 300], similarly employing ReLU and dropout.

The mean squared errors (MSE) were computed for each output physical quantity ($T_{center}$, $v_{center}$, $k_{center}$), and a composite loss function with $L_2$ regularization was formed.

Results and Discussion

CFD simulations with 5,000 different combinations of branch inputs were performed on AMD Ryzen 3900X CPU for data generation.

Model Performance

The MIONet model was trained using the Adam optimization algorithm with a learning rate of 0.001 and an $L_2$ regularization term. A 5-fold cross-validation strategy was implemented to assess the model's performance and prevent selection bias. The test results revealed the relative $L_2$ error of $0.2\%$, $0.8\%$, and $1.4\%$ for $T_{center}$, $v_{center}$, $k_{center}$, respectively.

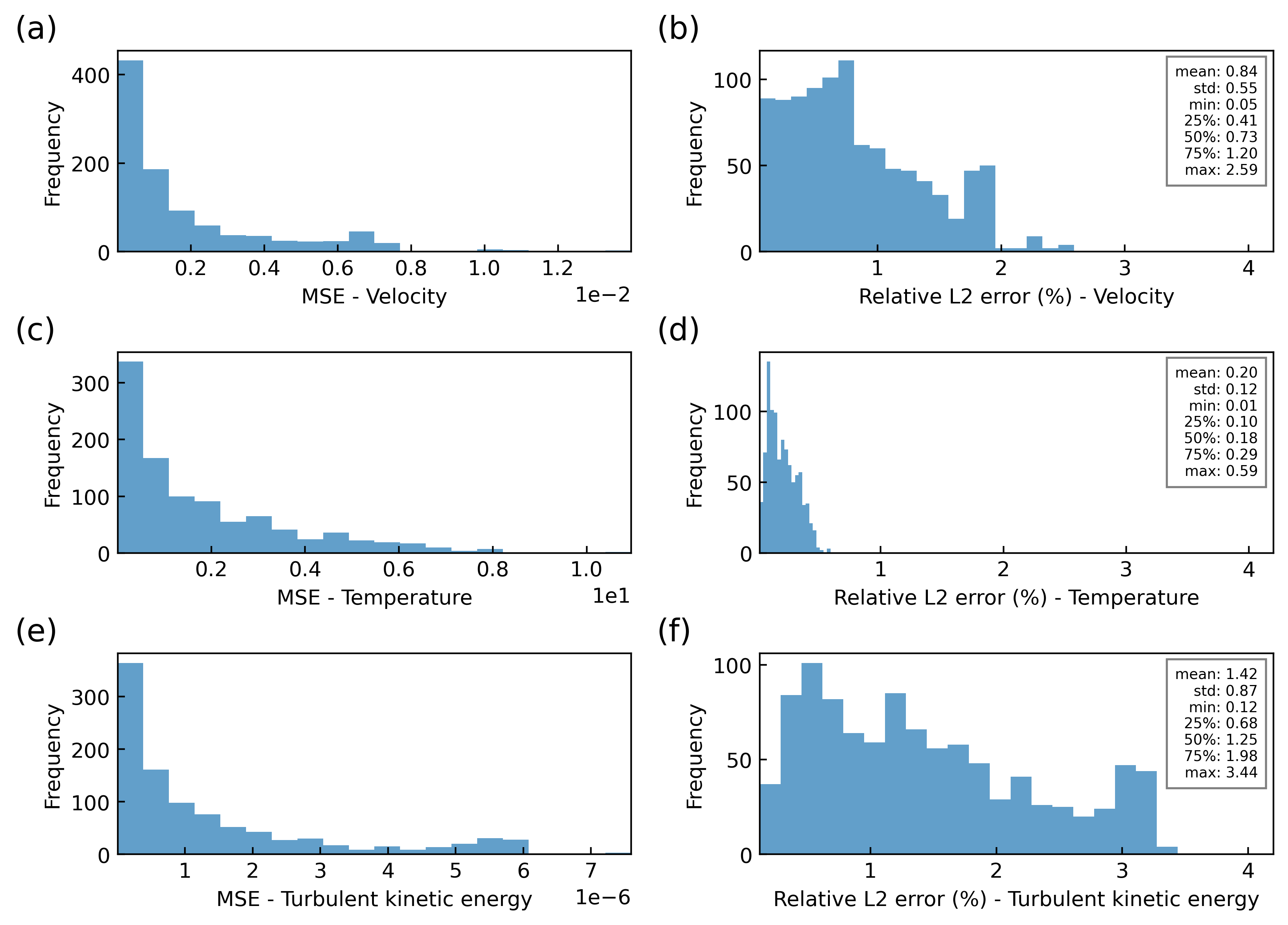
Figure 4: Distribution of model performance metrics for MIONet on the test dataset. Panels (a), (c), and (e) show histograms of the MSE for velocity, temperature, and turbulent kinetic energy predictions, respectively. Panels (b), (d), and (f) represent the histograms of the relative $L_2$ error percentage for the same respective quantities. Statistical summaries, including mean, standard deviation, and quantiles, are displayed in the insets for relative $L_2$ errors.

Figures 5, 6, and 7 present the velocity, temperature, and turbulence kinetic energy predictions from the MIONet model compared to the ground truth data obtained from CFD simulations. The results indicate that the MIONet model can accurately predict the distributions with minimal deviation from the CFD results.

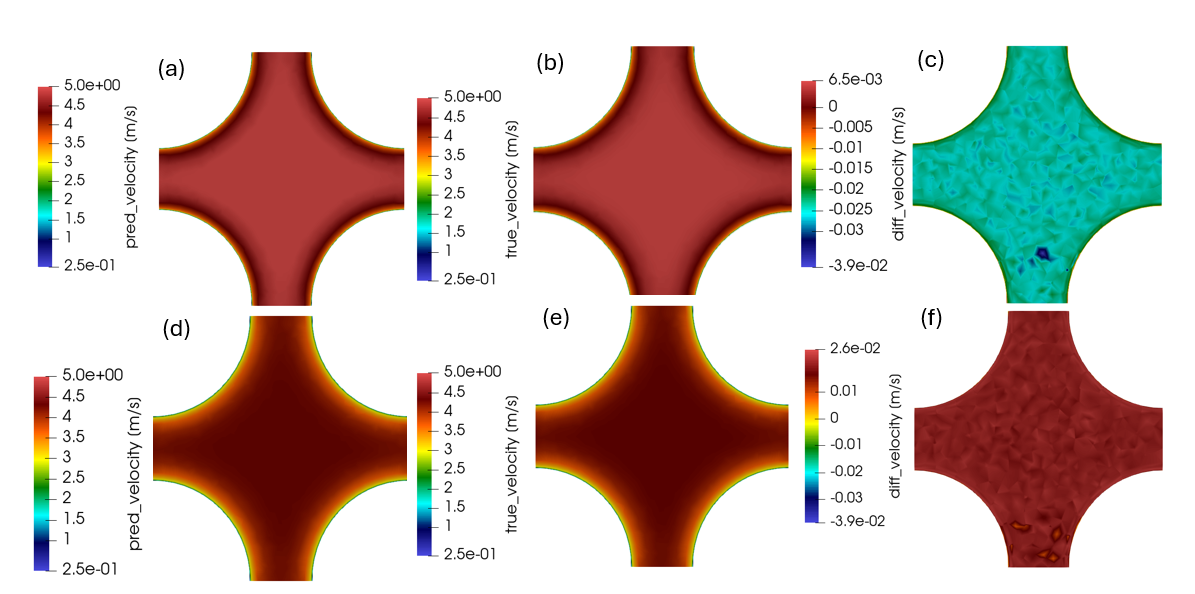
Figure 5: MIONet velocity predictions compared to ground truth data. Panels (a) and (d) show the predicted velocity distributions for the best and worst test cases, respectively. Panels (b) and (e) display the corresponding ground truth data. Panels (c) and (f) depict the absolute difference between the predictions and ground truth.

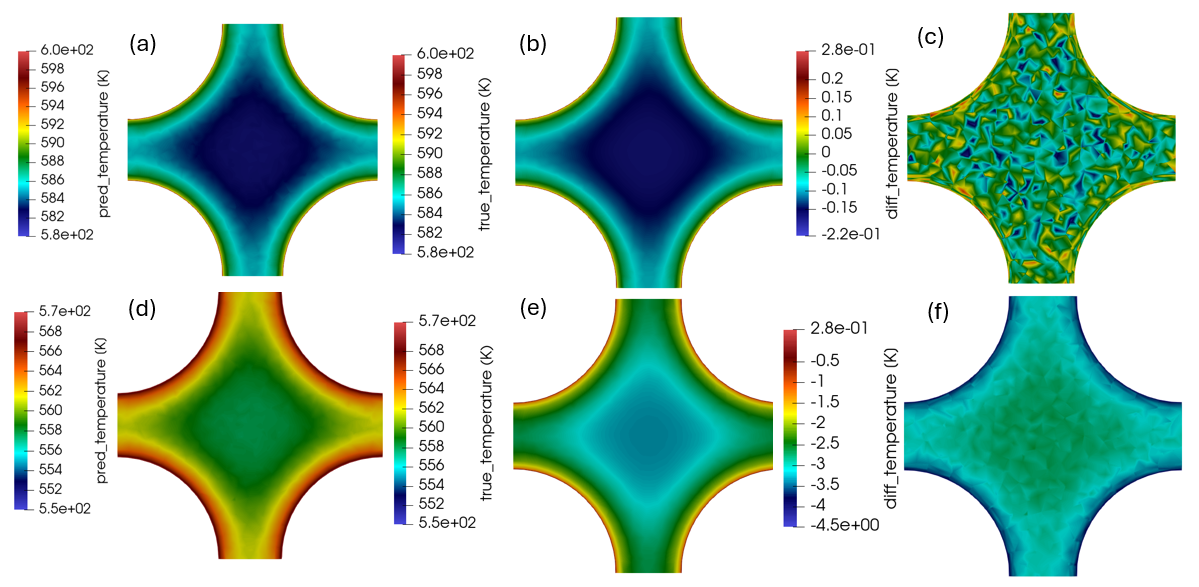
Figure 6: MIONet temperature predictions compared to ground truth data. Panels (a) and (d) show the predicted temperature distributions for the best and worst test cases, respectively. Panels (b) and (e) display the corresponding ground truth data. Panels (c) and (f) depict the absolute difference between the predictions and ground truth.

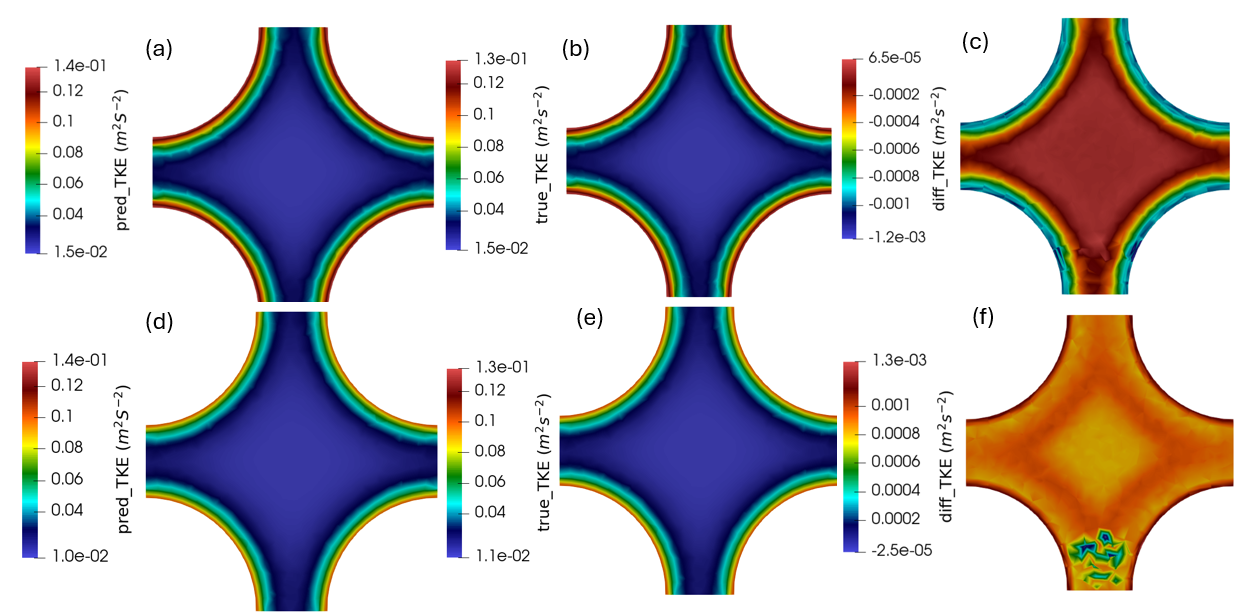
Figure 7: MIONet turbulence kinetic energy predictions compared to ground truth data. Panels (a) and (d) show the predicted energy distributions for the best and worst test cases, respectively. Panels (b) and (e) display the corresponding ground truth data. Panels (c) and (f) depict the absolute difference between the predictions and ground truth.

Computational Efficiency

The MIONet inference exhibits a lower inference time of about $5.24 \times 10^{-3}$ seconds compared to an average computation time of approximately 587 seconds for the CFD simulations. This difference highlights the MIONet model's potential for enabling real-time operational decision-making. The MIONet architecture generalizes well to new scenarios without necessitating constant retraining.

Conclusions

This paper introduces an approach to real-time monitoring of complex energy systems using MIONet virtual sensors. The MIONet-based surrogate model, trained on high-fidelity simulations, demonstrated remarkable inference speed without retraining, predicting temperature, velocity, and turbulence kinetic energy distributions within a PWR subchannel and outperforming conventional CFD simulations by over 100,000 times. The proposed method enables the inference of critical parameters at inaccessible locations to physical sensors.

Future research will explore broader applications of this technology, focusing on further integrating physics-informed constraints into the MIONet architecture and extending the model to handle time-series input functions.