Critical Phase Transition in Large Language Models (2406.05335v2)

Abstract: LLMs have demonstrated impressive performance. To understand their behaviors, we need to consider the fact that LLMs sometimes show qualitative changes. The natural world also presents such changes called phase transitions, which are defined by singular, divergent statistical quantities. Therefore, an intriguing question is whether qualitative changes in LLMs are phase transitions. In this work, we have conducted extensive analysis on texts generated by LLMs and suggested that a phase transition occurs in LLMs when varying the temperature parameter. Specifically, statistical quantities have divergent properties just at the point between the low-temperature regime, where LLMs generate sentences with clear repetitive structures, and the high-temperature regime, where generated sentences are often incomprehensible. In addition, critical behaviors near the phase transition point, such as a power-law decay of correlation and slow convergence toward the stationary state, are similar to those in natural languages. Our results suggest a meaningful analogy between LLMs and natural phenomena.

• The paper identifies a critical phase transition at T≈1 in GPT-2, marking a shift from ordered to disordered text structures.
• Systematic temperature variations and rigorous statistical analyses uncover polynomial decay of correlations characteristic of critical phenomena.
• Power spectrum and PCA analyses demonstrate how distinct textual structures emerge and dissolve, guiding optimal tuning of language models.

Critical Phase Transition in LLMs

The paper "Critical Phase Transition in a LLM," explores the presence of critical phase transitions within the dynamics of LLMs, specifically focused on models such as GPT-2. By drawing analogies with phase transitions in statistical physics, the authors examine how varying the temperature parameter leads to qualitative transitions in text generation. This essay provides an in-depth analysis of their findings, the methodologies employed, and their implications for understanding LLMs.

Introduction to Phase Transitions in LLMs

LLMs, like GPT-2, are known to perform differently across various tasks as a function of their hyperparameters, notably the temperature parameter, which scales the logits of tokens. The paper argues this parameter induces a phase transition, similar to those seen in physical systems such as the Ising model. As temperature changes, these models show sharp transitions in text structures from ordered (repetitive and predictable) at low temperatures to disordered (incomprehensible) at high temperatures.

The authors conceptualize this transition as a phase transition characterized by singular changes in statistical measures such as correlation decay. Evidence is provided showing that at a critical temperature $T_c \approx 1$, the model exhibits behaviors typical of critical phenomena. Below $T_c$, long-range correlations and repetitive structures manifest, whereas above this value, such structures dissipate.

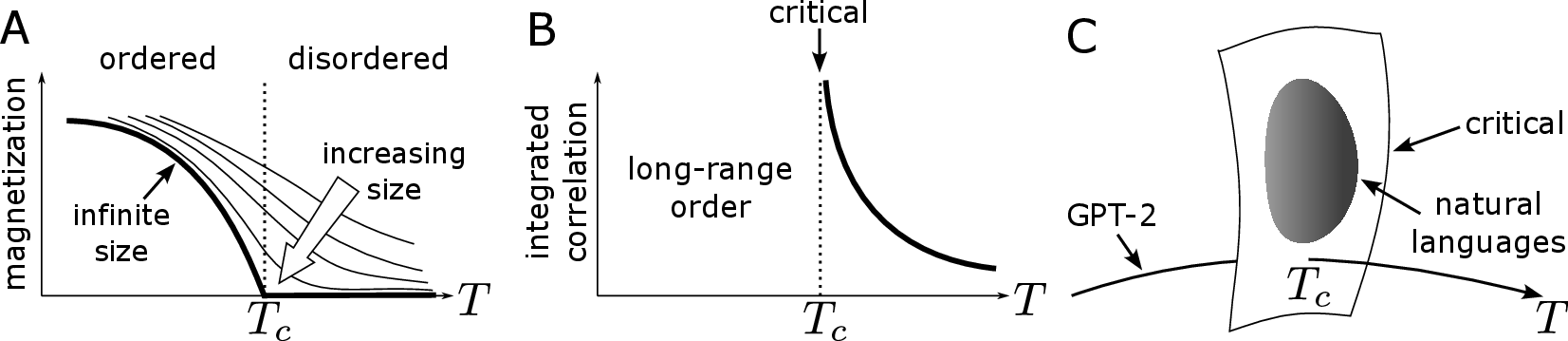
Figure 1: Analogies between phase transitions in physics and analogous phenomena in GPT-2, showcasing the transition from ordered to disordered phase at critical temperature $T_c$.

Methodology and Analysis

Experimental Setup

The authors employed the Hugging Face Transformers library for GPT-2 and utilized POS (part-of-speech) tagging to transform generated texts into sequences that facilitate measurement of statistical properties. The sampling process involved varying the temperature while keeping the starting token fixed, allowing the authors to systematically explore sequence dynamics over temperature changes. A substantial dataset of generated sequences was analyzed to calculate various statistical metrics.

Correlation and Integrated Correlation

A primary focus was the behavior of time correlations between tags in the sequences. The analysis of correlation functions, particularly for proper nouns (PROPN), revealed how at $T = 1$, correlations decay polynomially, indicating a critical slowing down characteristic of phase transitions.

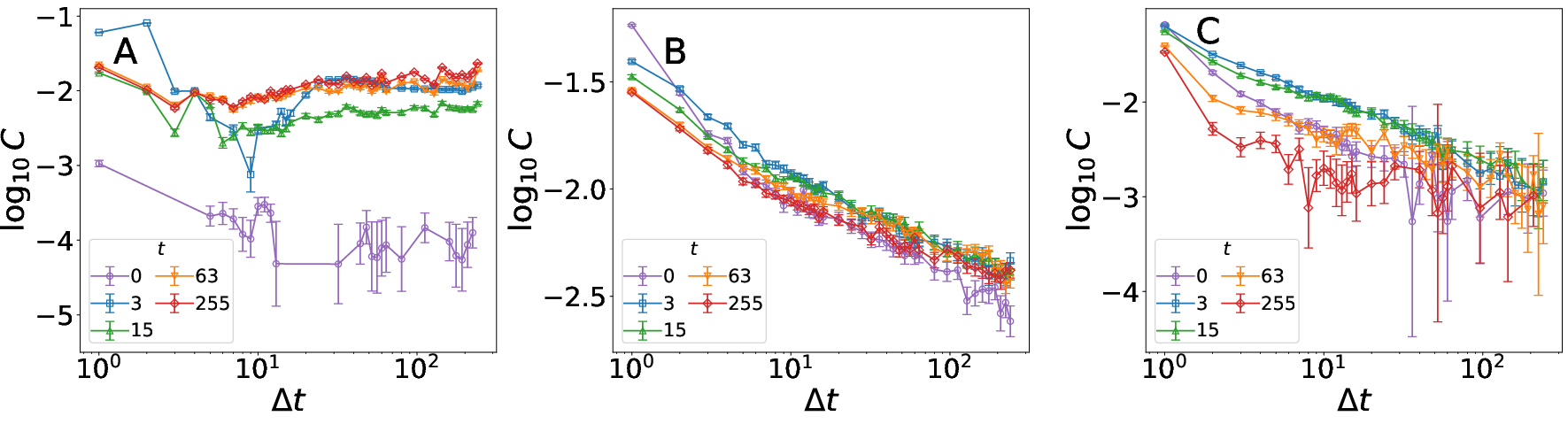
Figure 2: Correlation function $C(t, t+\Delta t)$ at different temperatures, highlighting critical behavior at $T = 1$.

The integrated correlation $\tau$ demonstrated divergent properties at low temperatures, suggesting a long-range order. This was contrasted with high temperatures, where correlations did not display simple exponential decay yet were finite, indicating complex but unstructured high-temperature phases.

Power Spectrum and Sequence Dynamics

The power spectrum analyses provided insights into the inherent order at different phases. At low temperatures, many distinct Fourier modes emerged, signifying structured repetitions. Near the critical temperature, these peaks dissipate, reflecting the loss of order and predicting the model's transition through different regimes of textual coherence.

(Figure 3)

Figure 3: Power spectrum $S(\omega)$ indicating the emergence of long-range order at low temperatures.

Additionally, the time evolution of probability distributions of POS tags further supports that at $T_c$, the dynamics were significantly slowed, hinting at transitory natural language behavior before reaching a stationary state. Principal Component Analysis (PCA) aided in visualizing these transitions, confirming significant shifts in principal components that correspond to meaningful textual structures.

Implications and Future Prospects

The identification of critical transitions in LLMs has profound implications for their practical use and evaluation. Understanding these phase transitions can enhance the tuning of LLMs for specific tasks across various domains by identifying temperature ranges that optimize performance. Furthermore, this framework provides a novel approach to evaluate LLM efficacy using statistical measures, thus offering a robust alternative to existing benchmarks.

Theoretically, these results open pathways for exploring universality classes in LLM phase transitions, akin to those in statistical physics. Future work could explore defining critical exponents specific to LLMs and investigating how variations in architecture or corpus impact these transitions.

Conclusion

This paper's investigation into the phase transition phenomena in LLMs like GPT-2 has offered new insights into their functional and structural complexities. By drawing parallels to critical phenomena in physics, the authors provide a compelling case for redefining how these models are understood and optimized, pointing towards a future where AI systems are finely tuned for critical coherence and stability.