Deep Extrinsic Manifold Representation for Vision Tasks (2404.00544v1)

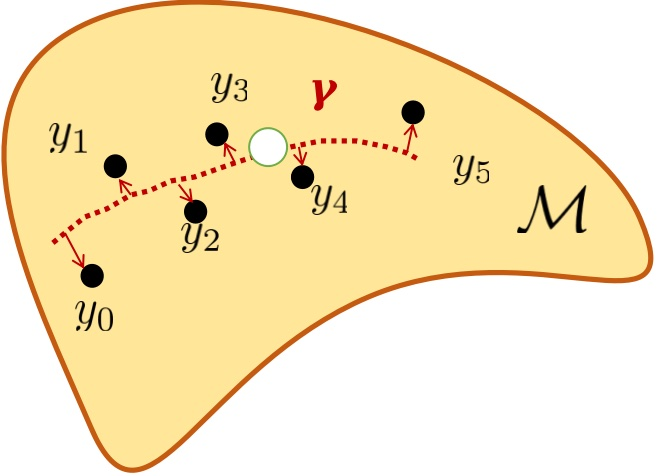
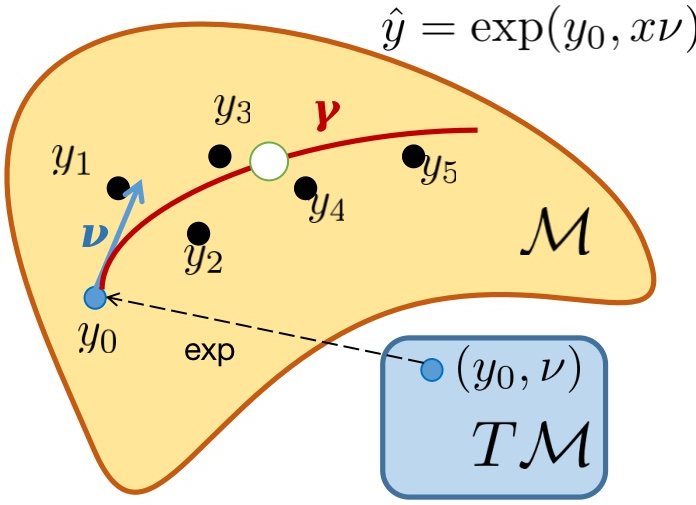
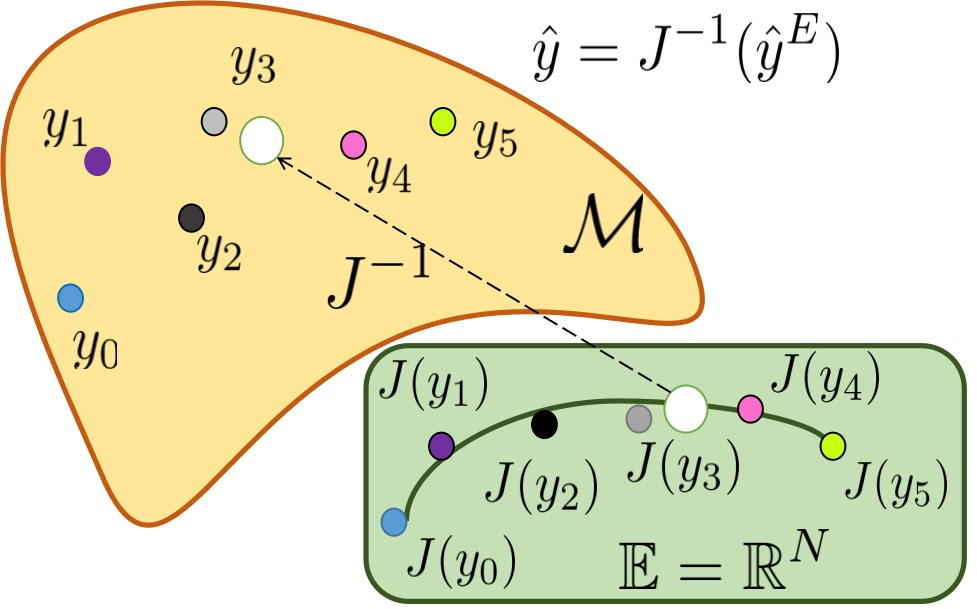
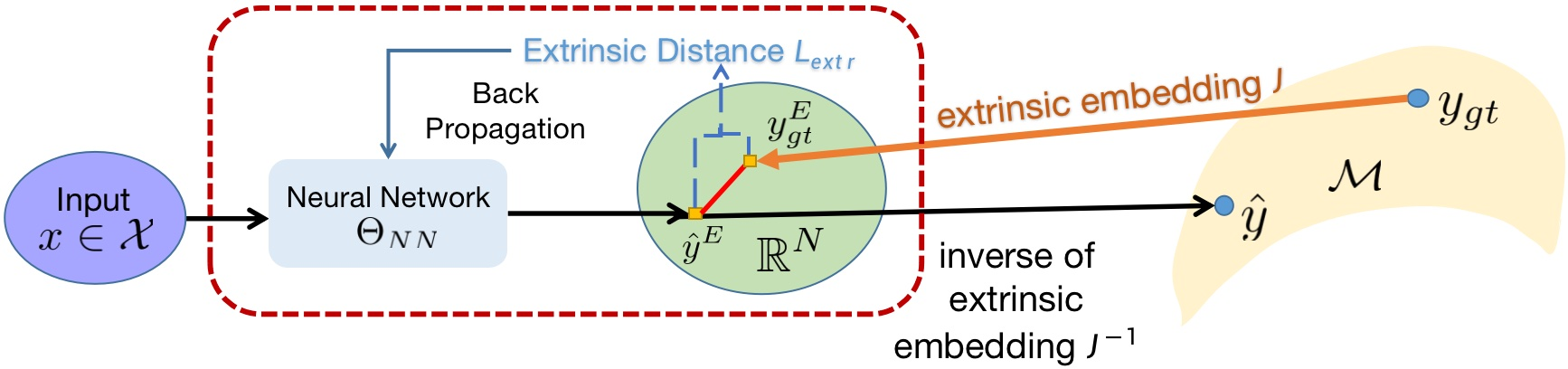
Abstract: Non-Euclidean data is frequently encountered across different fields, yet there is limited literature that addresses the fundamental challenge of training neural networks with manifold representations as outputs. We introduce the trick named Deep Extrinsic Manifold Representation (DEMR) for visual tasks in this context. DEMR incorporates extrinsic manifold embedding into deep neural networks, which helps generate manifold representations. The DEMR approach does not directly optimize the complex geodesic loss. Instead, it focuses on optimizing the computation graph within the embedded Euclidean space, allowing for adaptability to various architectural requirements. We provide empirical evidence supporting the proposed concept on two types of manifolds, $SE(3)$ and its associated quotient manifolds. This evidence offers theoretical assurances regarding feasibility, asymptotic properties, and generalization capability. The experimental results show that DEMR effectively adapts to point cloud alignment, producing outputs in $ SE(3) $, as well as in illumination subspace learning with outputs on the Grassmann manifold.

• The paper introduces DEMR, a technique embedding manifold outputs extrinsically into Euclidean space to optimize deep networks efficiently.
• It leverages learnable linear layers to map between Euclidean and manifold spaces, enabling adaptive handling of non-Euclidean data in vision tasks.
• Empirical evaluations on tasks like pose regression and illumination subspace estimation demonstrate superior performance and improved generalization.

Deep Extrinsic Manifold Representation for Vision Tasks

The paper "Deep Extrinsic Manifold Representation for Vision Tasks" explores the novel integration of extrinsic manifold embeddings into deep neural networks (DNNs) to address the challenge of producing manifold-valued representations from neural network outputs. This research focuses specifically on vision tasks where data typically resides within non-Euclidean spaces, and standard DNN architectures struggle to maintain the geometric structure required for accurate manifold representation.

Problem Statement and Approach

Context and Motivation

In domains such as robotics and medical imaging, data often exists in non-Euclidean geometric spaces necessitating specialized processing to maintain their inherent geometric properties. Traditional DNNs output feature vectors in Euclidean spaces, which can be inefficient for tasks requiring outputs like probability distributions or rigid motion estimations, as exemplified by pose regressions and illumination subspace learnings.

Figure 1: Manifold regression explores the relationship between a manifold-valued variable and a value in vector space.

Deep Extrinsic Manifold Representation (DEMR)

DEMR is introduced as a method to embed manifold outputs extrinsically while leveraging Euclidean spaces for optimization. DEMR avoids the direct optimization of geodesic losses, focusing instead on optimizing function representations within an embedded Euclidean space. This approach empowers adaptability across various architectures without compromising existing DNN structures.

Figure 2: DEMR pipeline, with black arrows indicating the forward process, and optimization in the red box.

Implementation Insights

Methodology

DEMR operates by embedding the manifold into a higher-dimensional Euclidean space using an extrinsic embedding function, $J(\cdot)$. This translation allows standard DNN architectures to maintain traditional output processing while seamlessly projecting outputs back to the manifold space. The geodesic loss calculation is replaced by a more tractable extrinsic loss formulation computed within the Euclidean geometry, enabling smoother optimization and training processes.

Projection Mechanism

The projection from the Euclidean representations to the manifold preimage is accomplished through learnable linear layers, enhancing the flexibility and scalability of DEMR across different network architectures. This learnable process replaces deterministic operations typically required in manifold regressions, aligning closely with iterative adaptation seen in modern neural network training paradigms.

Theoretical Contributions

Geometric Properties

Ensuring geometric conformity between intrinsic manifold structures and their extrinsic embeddings is essential. The paper asserts that the preservation of geometric continuity through the use of bilipschitz embeddings enables mapping outputs between Euclidean and manifold spaces efficiently, thus supporting adaptation across a wide array of input configurations.

Maximum Likelihood Estimation

DEMR effectively approximates maximum likelihood estimations (MLE) for data lying on specific manifolds, particularly $SO(3)$ and $SE(3)$, due to the choice of extrinsic embeddings. This characteristic makes DEMR suitable for tasks demanding precise estimations such as pose regressions and transformations.

Empirical Evaluation

Vision Tasks

The paper conducts rigorous evaluations on canonical vision tasks such as affine motion estimation on $SE(3)$ for point clouds and illumination subspace estimation on the Grassmann manifold. DEMR demonstrates superior performance compared to intrinsic manifold optimization methods and unstructured neural network outputs.

Figure 3: The cumulative distributions comparison of position errors for the pose regression task on SE(3).

Generalization

DEMR exhibits heightened generalization capabilities by efficiently extrapolating trained models to unseen geometrical configurations. This improvement in generalization illustrates the advantage of adopting extrinsic embeddings for manifolds over conventional methods.

Conclusion

The presented work illuminates the promising potential of integrating extrinsic manifold representations into deep learning architectures, specifically enhancing the computational efficiency and adaptability required for complex vision tasks. Future research directions may include exploring parameterized forms of extrinsic embeddings to automatically tailor manifold representations within varied neural network environments. By incorporating structured geometric understanding into DNN outputs, DEMR paves the path for more robust, scalable AI applications across diverse fields.