- The paper introduces a novel PGDC method that defines and benchmarks the 'knowledge boundary' in LLMs by optimizing prompt sensitivity.
- It demonstrates that PGDC outperforms baseline methods across various datasets, fulfilling key criteria like universality, truthfulness, and robustness.
- Experimental results reveal that PGDC minimizes the generation of fake knowledge and finds optimal prompts in fewer iterations, providing a more comprehensive evaluation framework.
Benchmarking Knowledge Boundary for LLMs
The paper "Benchmarking Knowledge Boundary for LLMs: A Different Perspective on Model Evaluation" (2402.11493) introduces a novel evaluation paradigm for LLMs based on the concept of a "knowledge boundary." This boundary aims to capture the extent of a model's knowledge by identifying the range of prompts that can elicit correct answers, addressing the prompt sensitivity issue prevalent in existing evaluation methods. The authors propose a Projected Gradient Descent method with Constraints (PGDC) to optimize prompts and explore these knowledge boundaries, demonstrating its superior performance compared to baseline methods across several datasets and models.
Knowledge Boundary and its Requirements
The paper identifies that existing LLM evaluation benchmarks often rely on fixed questions or limited paraphrases, failing to account for the prompt sensitivity of LLMs. This can lead to unreliable and incomplete assessments of a model's knowledge capabilities. To address this, the authors introduce the concept of a knowledge boundary, which encompasses both prompt-agnostic and prompt-sensitive knowledge.
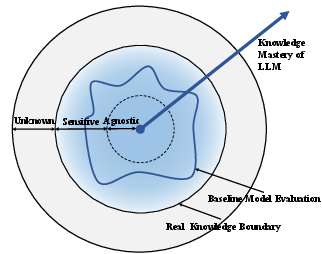
Figure 1: Illustration of three classes of knowledge based on the model's mastery of knowledge in different textual forms.
The knowledge boundary represents the spectrum of textual forms or prompts that can successfully elicit a correct answer from the LLM (Figure 1). The authors define four key requirements for an algorithm designed to calculate knowledge boundaries:
- Universality: The method should be applicable to a wide range of LLMs, regardless of size or architecture.
- Truthfulness: The constructed prompts should maintain the same semantics as the original question, avoiding changes in subject or relation.
- Robustness: The method's effectiveness should correlate with the LLM's actual knowledge capacity, avoiding the generation of appropriate prompts for unanswerable knowledge.
- Optimality: The algorithm should identify as much prompt-sensitive knowledge as possible within the LLM.
Projected Gradient Descent Method with Constraints (PGDC)
To explore the knowledge boundary of LLMs, the authors propose PGDC, an algorithm that optimizes prompts through gradient descent while adhering to semantic constraints. PGDC operates by mapping the prompt in text form to a continuous embedding space, updating the embedding through gradient descent based on a defined loss function, and projecting the embedding back to discrete tokens.
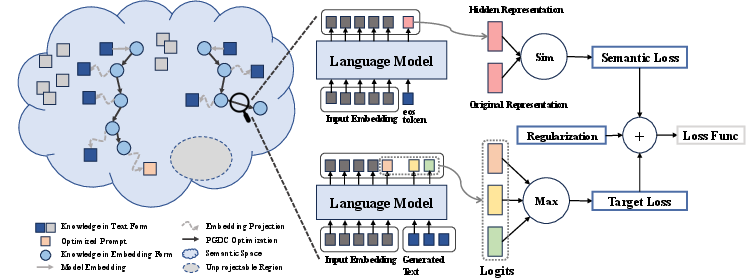
Figure 2: An illustration of the PGDC method, showing the overall framework of optimization and loss calculation.
The optimization process incorporates a target loss, a semantic loss, and a regularization term (Figure 2). The target loss penalizes unsuccessful generation of the correct answer, while the semantic loss measures the distance between the optimized prompt and the original prompt to maintain semantic consistency. The regularization term prevents the embedding from entering unprojectable regions, ensuring that the optimized prompt can be effectively transformed back into discrete tokens. The final loss function is formulated as:
L(X)=L(X,A)+λ1R(X,Q)+λ2δ(X).
Here, L(X,A) is the target loss, R(X,Q) is the semantic loss, δ(X) is the regularization term, and λ1 and λ2 are penalty factors. The proximal projection step transforms the embedding back to text space based on a vector distance threshold, allowing for flexible transformation between the embedding and text spaces.
Experimental Evaluation and Results
The authors conducted experiments on several datasets, including KAssess, PARAREL, COUNTERFACT, and ALCUNA, to evaluate the performance of PGDC against baseline methods such as zero-shot prompting, few-shot prompting, and a discriminator-based approach. The models used in the experiments included GPT-2, GPT-J, LLaMA2, and Vicuna.
The results demonstrate that PGDC consistently outperforms the baseline methods on common knowledge benchmarks, indicating its ability to identify more comprehensive knowledge boundaries. Specifically, PGDC achieves the highest performance on common knowledge benchmarks on almost all LLMs. The experiments on unanswerable knowledge benchmarks (COUNTERFACT and ALCUNA) show that PGDC introduces relatively limited fake knowledge, meeting the robustness requirement. This demonstrates the optimality and universality of PGDC. Manual evaluation confirms that the prompts generated by PGDC are generally semantically consistent with the original questions, demonstrating truthfulness.
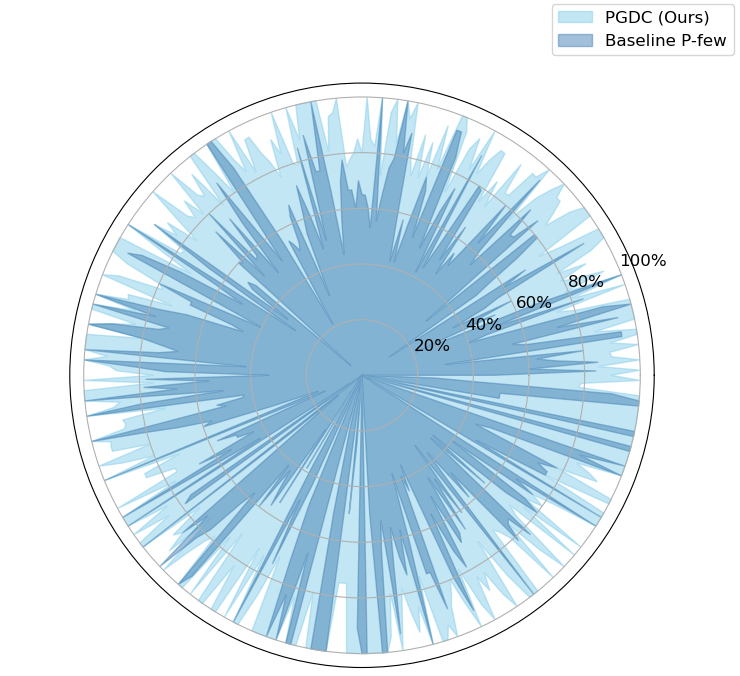
Figure 3: Knowledge boundaries of PGDC and baseline method P-few on KAssess using LLaMA2 model.
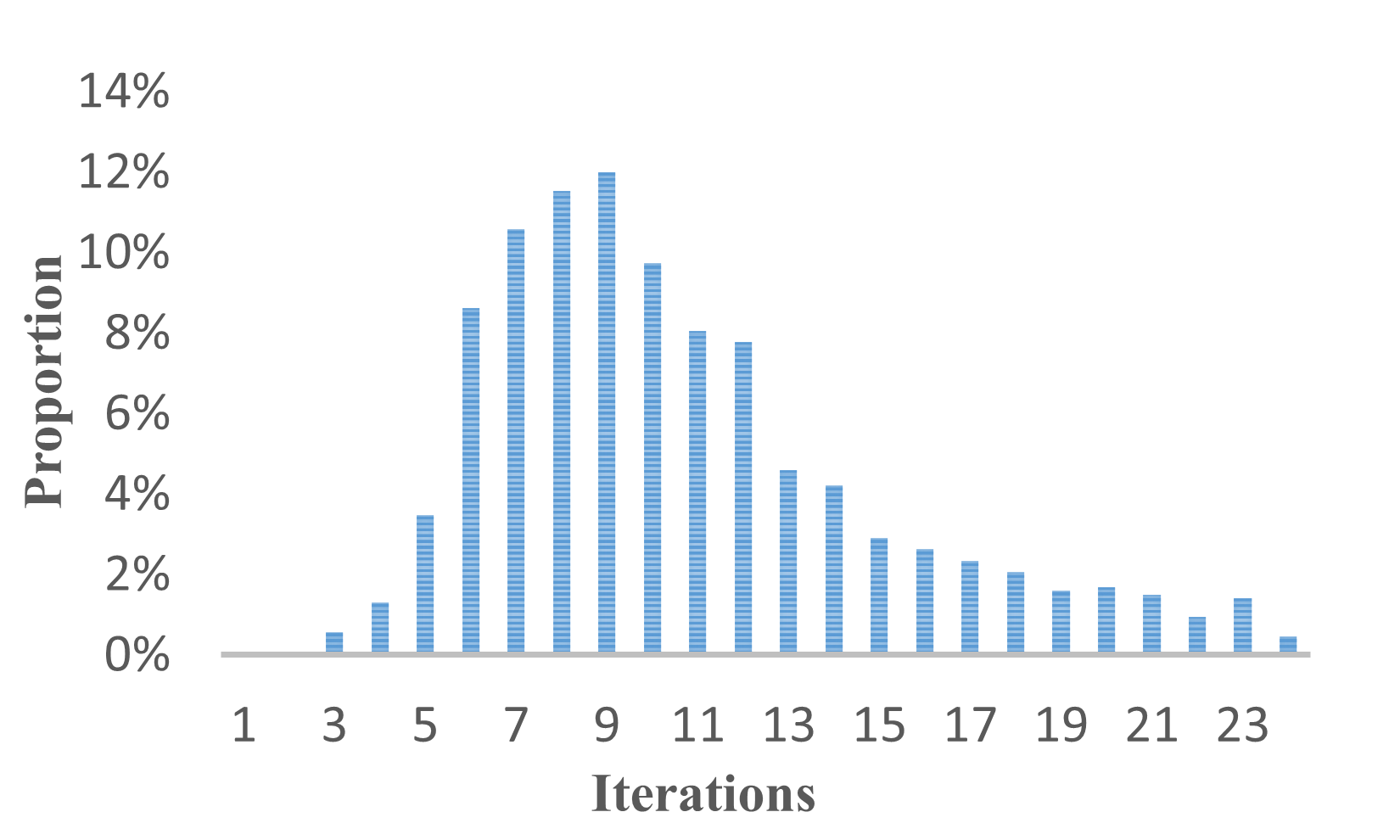
Figure 4: Iterations on KAssess to find the optimized prompt using PGDC with LLaMA2 model.
Further analysis reveals that evaluating LLMs with fixed questions or limited paraphrases is unreliable. The discrimination format is found to be less reliable than the cloze-style format, and different models exhibit preferences for different prompts. The knowledge boundaries obtained by PGDC can almost cover baselines (Figure 3). PGDC can find the optimal prompt for the majority of queries within 15 iterations (Figure 4).
Comparison with Prompt Optimization Methods
The authors compare PGDC with AutoPrompt, a representative prompt optimization method, on the CFACT dataset. The results show that AutoPrompt induces the model to output target answers on counterfactual datasets in a large percentage, suggesting that Autoprompt is more similar to an adversarial attack algorithm. PGDC, on the other hand, optimizes the prompt within the semantic constraint. Specifically, Autoprompt achieved 92.38%, 85.67%, 88.35%, and 33.09% success rates on the CFACT dataset for GPT-2, GPT-J, LLaMA2, and Vicuna, respectively, while PGDC achieved only 2.81%, 4.82%, 3.41%, and 3.50% success rates.
Application to MMLU Dataset
The authors apply PGDC to the MMLU dataset to evaluate LLMs across 30 refined domain knowledge areas. The questions in MMLU are modified from choice questions to a cloze format. The results show that Mistral has the largest knowledge boundaries overall, and LLaMA2 exceeds the other models in the engineering domain (Figure 5).
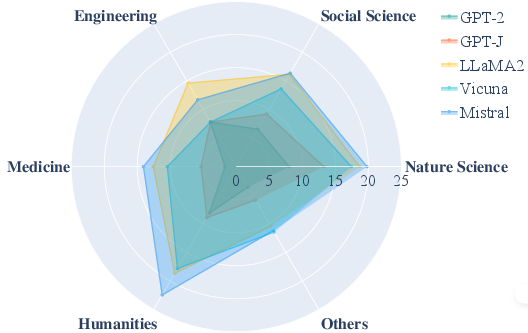
Figure 5: Knowledge boundaries of different domains of models on MMLU.
Conclusion
The paper presents a compelling argument for the limitations of traditional LLM evaluation methods and introduces a novel approach based on the concept of knowledge boundaries. The PGDC algorithm provides a practical and effective means of exploring these boundaries, offering a more comprehensive and reliable assessment of LLM knowledge capabilities. This work has significant implications for the development and evaluation of LLMs, paving the way for more accurate and robust benchmarks that can better reflect the true potential of these models. While the current work focuses on identifying unanswerable knowledge, future research could explore the nuances of prompt-sensitive knowledge to gain a more granular understanding of LLM capabilities.






