Beyond Chinchilla-Optimal: Accounting for Inference in Language Model Scaling Laws (2401.00448v2)

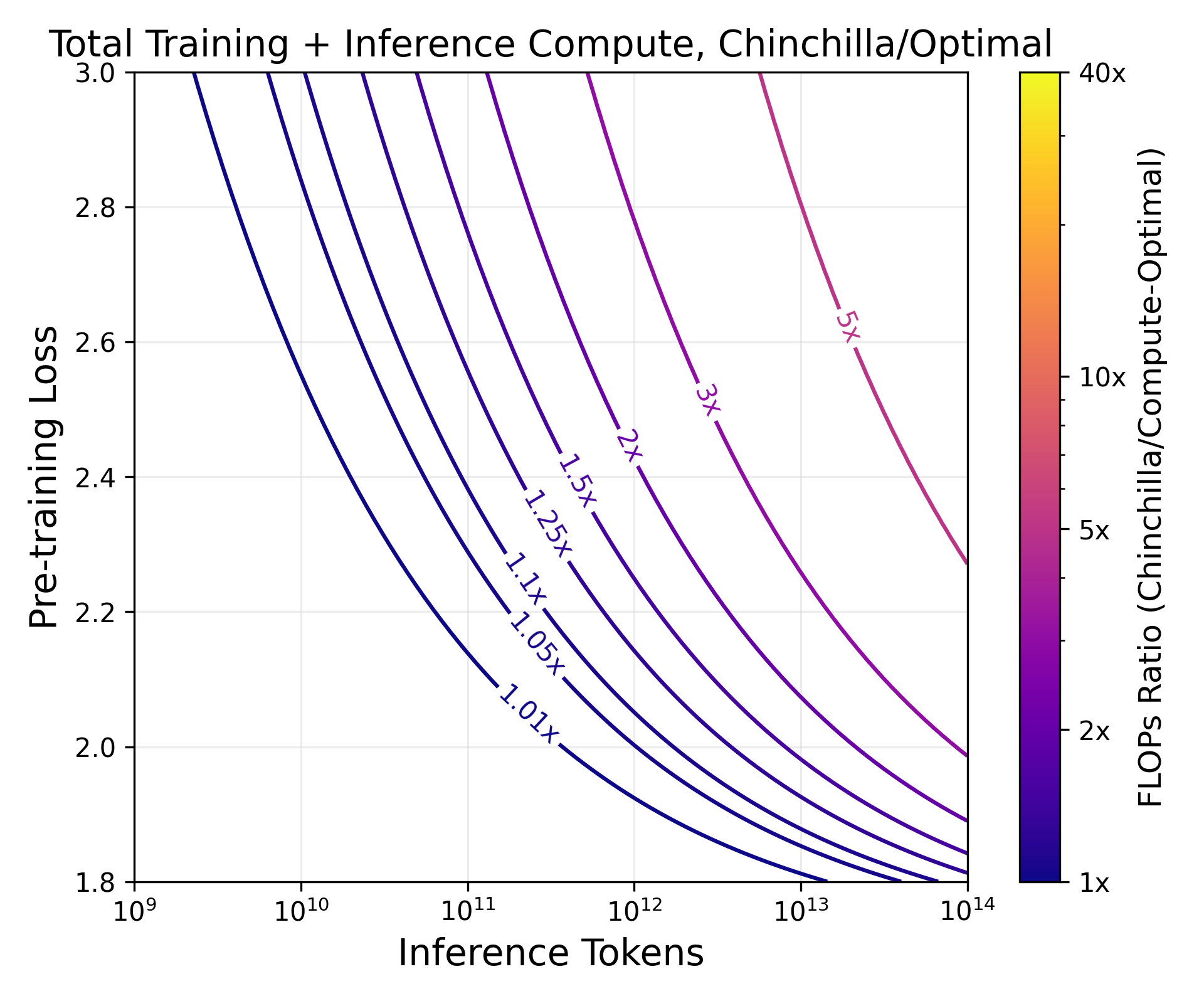
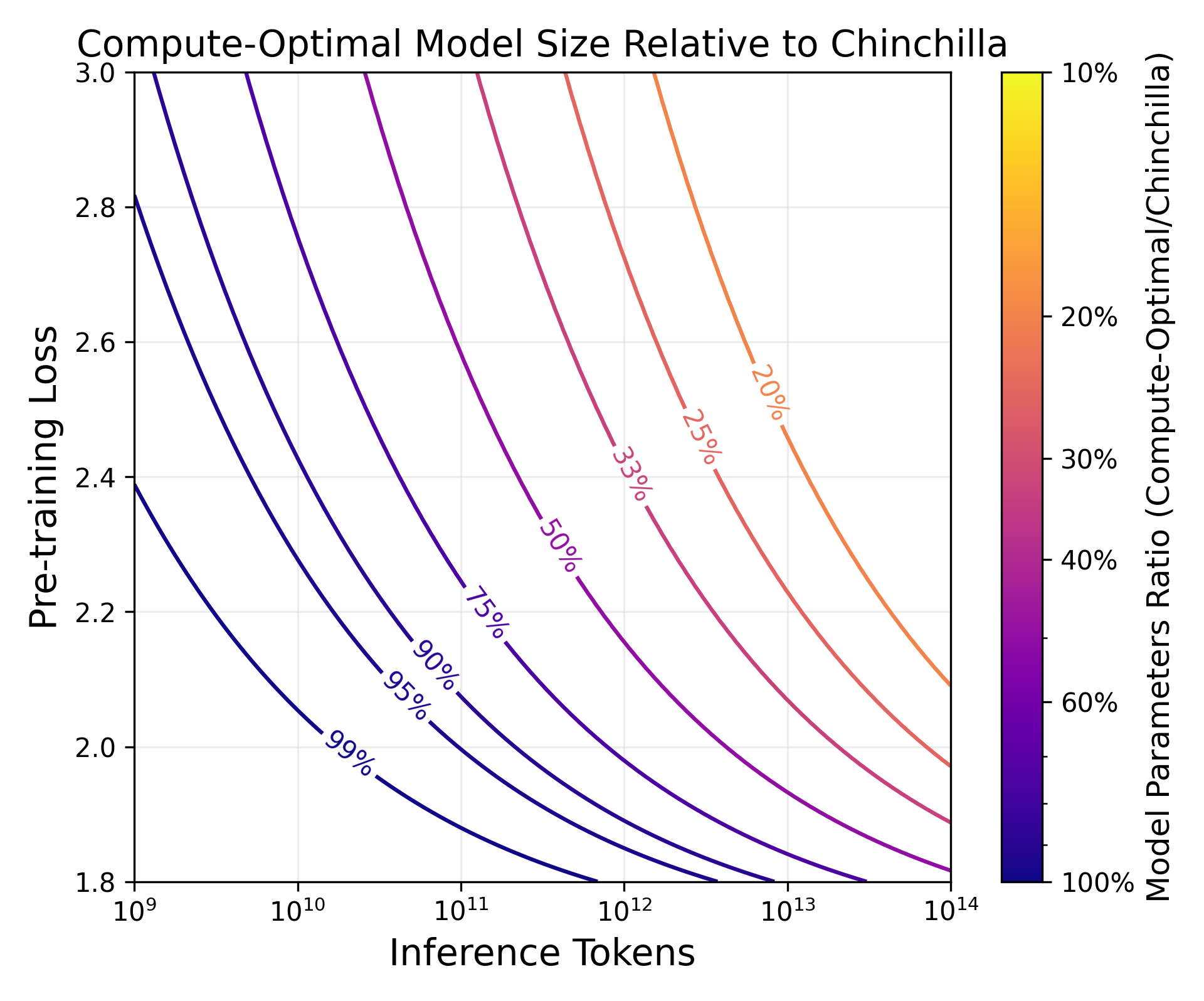
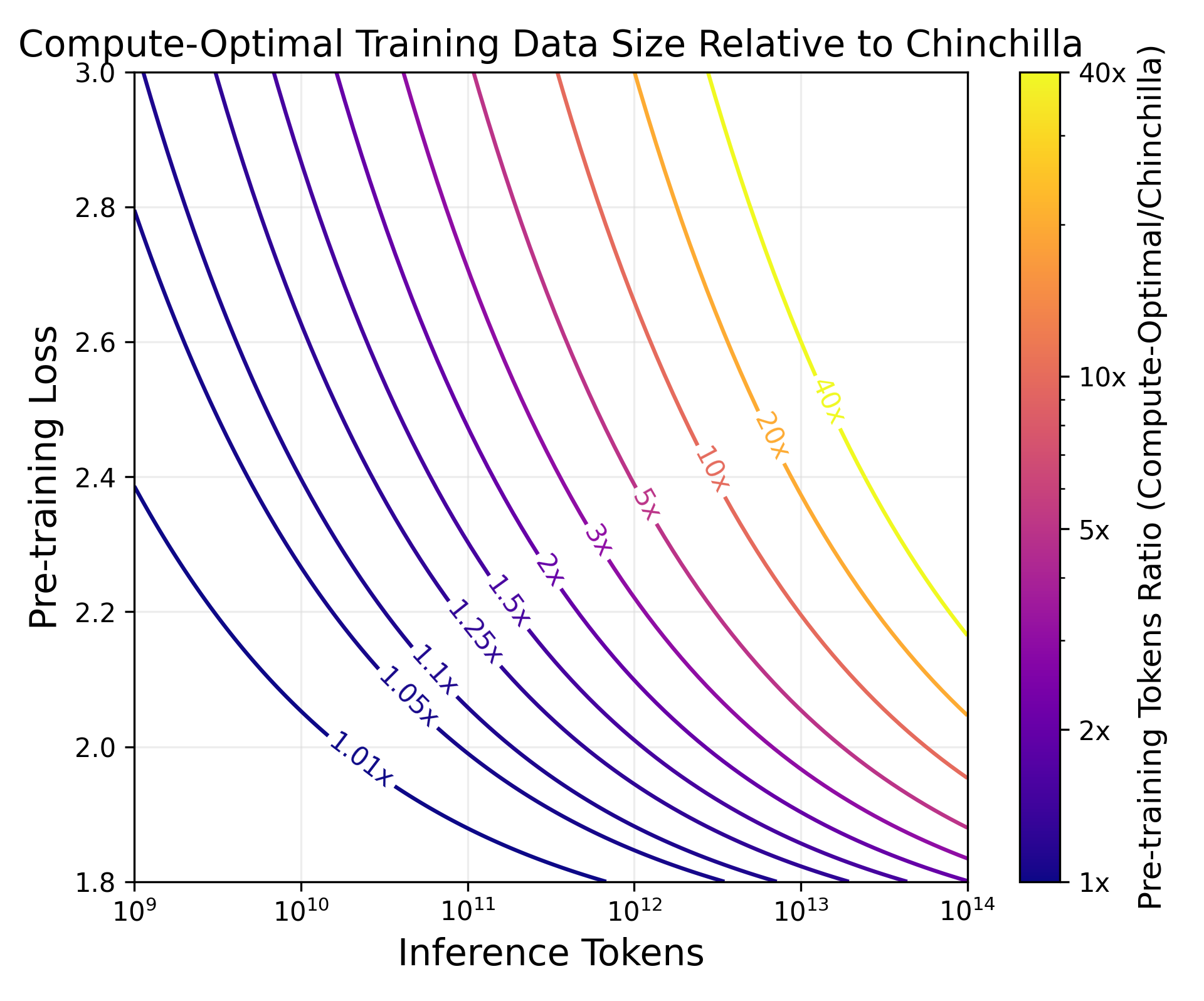
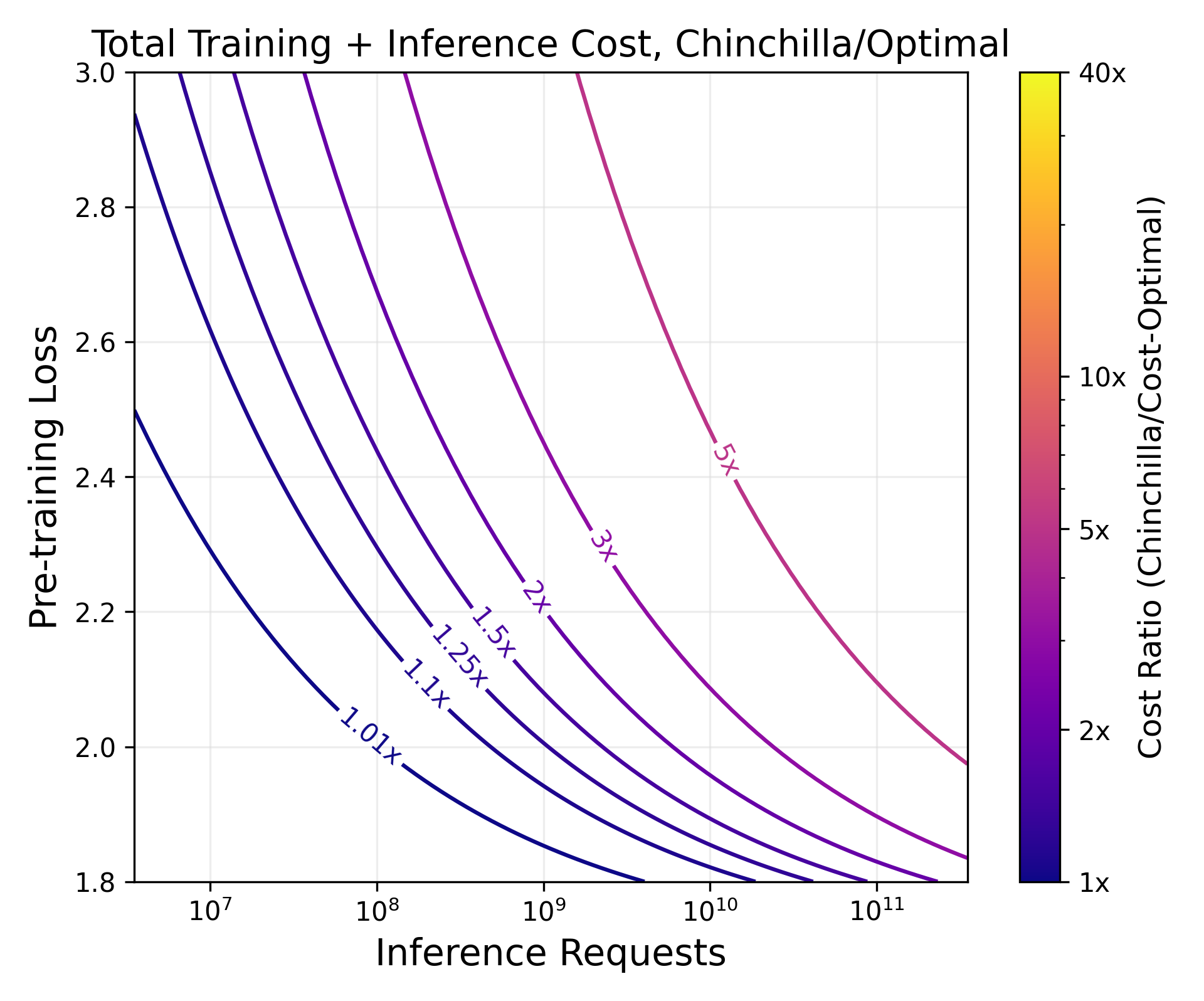
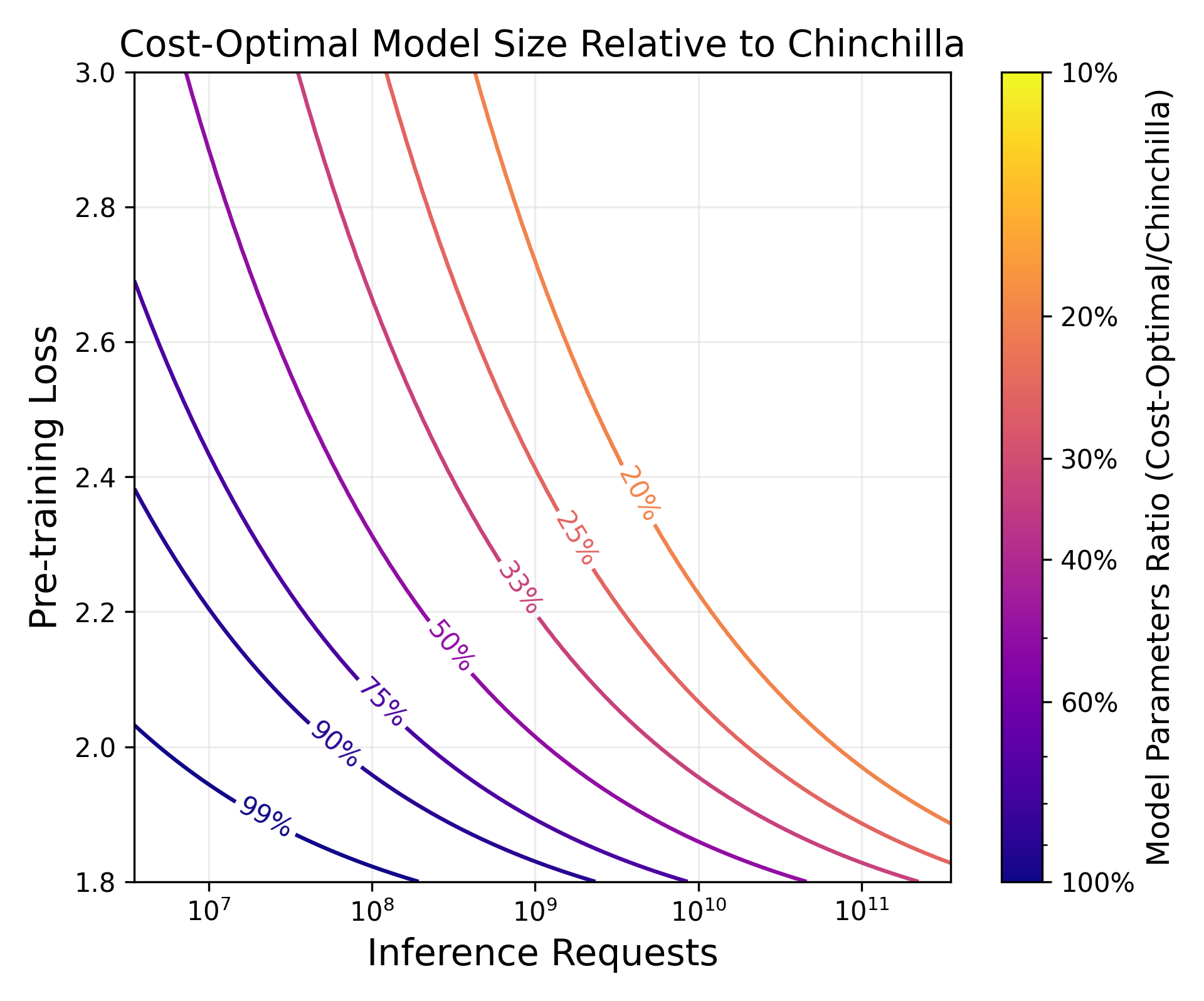
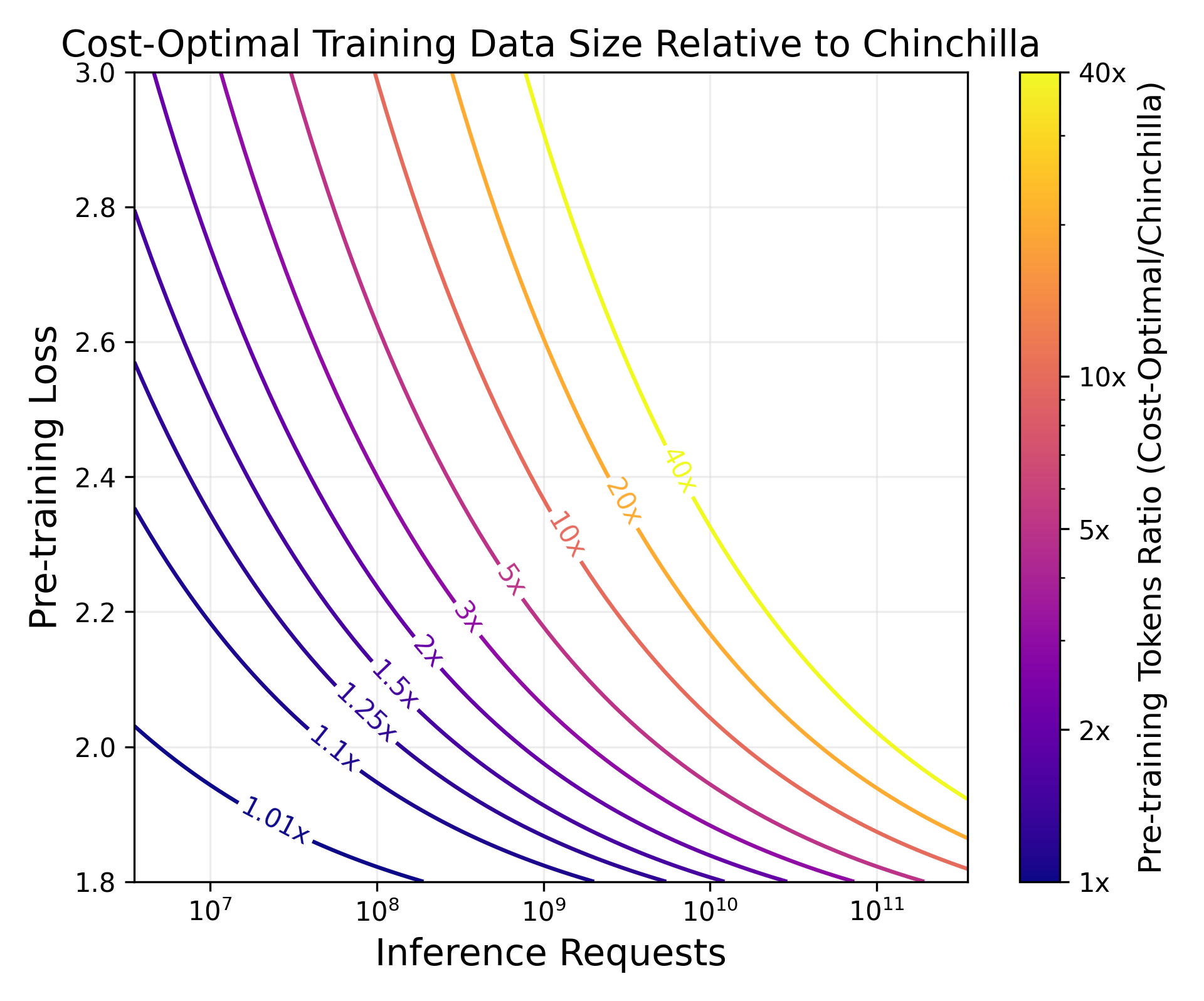
Abstract: LLM scaling laws are empirical formulas that estimate changes in model quality as a result of increasing parameter count and training data. However, these formulas, including the popular Deepmind Chinchilla scaling laws, neglect to include the cost of inference. We modify the Chinchilla scaling laws to calculate the optimal LLM parameter count and pre-training data size to train and deploy a model of a given quality and inference demand. We conduct our analysis both in terms of a compute budget and real-world costs and find that LLM researchers expecting reasonably large inference demand (~1B requests) should train models smaller and longer than Chinchilla-optimal. Furthermore, we train 47 models of varying sizes and parameter counts to validate our formula and find that model quality continues to improve as we scale tokens per parameter to extreme ranges (up to 10,000). Finally, we ablate the procedure used to fit the Chinchilla scaling law coefficients and find that developing scaling laws only from data collected at typical token/parameter ratios overestimates the impact of additional tokens at these extreme ranges.

• The paper introduces an adjusted scaling law that factors inference costs into LLM training, optimizing overall computational efficiency.
• It demonstrates that smaller, longer-trained models perform better under high inference demand by reducing floating-point operation usage.
• The study proposes a practical cost model that bridges training and inference expenses across varied hardware environments.

Introduction

LLMs have significantly impacted the field of artificial intelligence, especially in understanding and generating human language. As these models grow larger, it becomes crucial to understand the scaling laws that govern changes in model quality with increases in parameter count and training data. The Chinchilla scaling laws, coined by DeepMind, are a set of empirical formulas that estimate the optimal parameter count and pre-training data size for LLMs. While these have been influential in guiding model training, they focus primarily on training costs, neglecting inference costs, which can be substantial. This paper introduces a new approach to LLM scaling laws that incorporate inference costs to optimize both computational and financial resources.

Computational Optimality

The authors present an adjusted version of the Chinchilla scaling laws that take inference costs into account. They define model quality via cross-entropy loss and computational cost through floating-point operations (FLOPs). Their analysis shows that LLM practitioners expecting substantial inference demand should consider training models that are smaller and trained for longer periods than what would be recommended by Chinchilla laws. This adjusted framework implies that as inference requests increase, the total computational cost changes, skewing towards models that are trained with more data but have fewer parameters.

Estimating Real-World Cost Optimality

Focusing purely on minimizing FLOPs may not align with real-world conditions where various factors, such as hardware utilization and the costs associated with training versus inference, differ significantly. This paper extends the revisions to the Chinchilla scaling laws by including a model for estimating actual costs. The authors consider training and inference on different hardware types, the effects of model quantization before inference, and differences in utilization between training and inference. Real-world cost analysis suggests even greater emphasis on small and long-trained models to reduce inference costs, accounting for significant differences in utilization and costs of training versus inference.

Conclusion

The paper culminates in a revised set of scaling laws for LLMs that address both computational efficiency and real-world cost considerations. It argues for a more nuanced approach to model training that considers the lifespan and demand for inference, steering away from training the largest models possible towards more economically optimized solutions. While admitting the need for experimental validation and questioning whether these laws hold in extreme conditions, the authors establish a comprehensive platform for future work in LLM scaling, potentially affecting how future models are developed.