Training Chain-of-Thought via Latent-Variable Inference (2312.02179v1)

Abstract: LLMs solve problems more accurately and interpretably when instructed to work out the answer step by step using a ``chain-of-thought'' (CoT) prompt. One can also improve LLMs' performance on a specific task by supervised fine-tuning, i.e., by using gradient ascent on some tunable parameters to maximize the average log-likelihood of correct answers from a labeled training set. Naively combining CoT with supervised tuning requires supervision not just of the correct answers, but also of detailed rationales that lead to those answers; these rationales are expensive to produce by hand. Instead, we propose a fine-tuning strategy that tries to maximize the \emph{marginal} log-likelihood of generating a correct answer using CoT prompting, approximately averaging over all possible rationales. The core challenge is sampling from the posterior over rationales conditioned on the correct answer; we address it using a simple Markov-chain Monte Carlo (MCMC) expectation-maximization (EM) algorithm inspired by the self-taught reasoner (STaR), memoized wake-sleep, Markovian score climbing, and persistent contrastive divergence. This algorithm also admits a novel control-variate technique that drives the variance of our gradient estimates to zero as the model improves. Applying our technique to GSM8K and the tasks in BIG-Bench Hard, we find that this MCMC-EM fine-tuning technique typically improves the model's accuracy on held-out examples more than STaR or prompt-tuning with or without CoT.

• The paper demonstrates that the TRICE algorithm leverages latent-variable inference to fine-tune chain-of-thought reasoning in LLMs.
• It employs an MCMC-EM framework with a novel control-variate technique to reduce gradient variance and stabilize training.
• Experiments on GSM8K and BIG-Bench Hard show TRICE outperforms baselines like STaR, enhancing overall reasoning accuracy.

Training Chain-of-Thought via Latent-Variable Inference

The paper "Training Chain-of-Thought via Latent-Variable Inference" (2312.02179) proposes a novel fine-tuning strategy for improving the performance of LLMs in solving problems using chain-of-thought (CoT) prompting. The method addresses the challenge of sampling from the posterior of rationales conditioned on the correct answer, employing a Markov-chain Monte Carlo (MCMC) expectation-maximization (EM) framework enhanced with a control-variate technique to optimize variance in gradient estimates. The effectiveness of this approach is demonstrated on datasets such as GSM8K and BIG-Bench Hard, showing superior performance compared to baseline methods like STaR and direct tuning.

Introduction to Chain-of-Thought and Fine-Tuning

LLMs generally achieve better accuracy and interpretability when they are prompted to reveal their reasoning in a step-by-step CoT manner. Traditional techniques to enhance model performance involve supervised fine-tuning, which aligns model parameters by maximizing the likelihood of correct answers. However, applying CoT with this approach necessitates detailed rationales, which can be costly to produce manually. The paper introduces a method that optimizes the marginal log-likelihood of generating the correct answer, effectively averaging over all rationales without explicit supervision for each.

Methodology: TRICE Algorithm

The core of the proposed method is the TRICE algorithm, short for "Tuning Rationales with Independence-Chain Expectation-Maximization." TRICE operates by modeling CoT methods as probabilistic latent-variable models, where the objective is to maximize the marginal likelihood of answers given questions. Instead of focusing on the correct answer alone, TRICE treats the rationales as latent variables, applying MCMC-EM to sample these rationales.

Control-Variate Technique: TRICE introduces a variance reduction strategy that applies a novel control-variate approach, which ensures that the variance of the gradient estimator reduces to zero as model accuracy improves. This is crucial as it stabilizes the convergence of training by selectively scaling gradient contributions based on the correctness of sampled rationales.

Implementation Details: The algorithm deploys a rationalization memory that stores latent rationales, updated iteratively through MCMC steps. It uses a hinted guide distribution to initialize rationales, which are then refined using proposals from the model itself. The method emphasizes bootstrapping from datasets with only questions and answers, thus bypassing the need for manually annotated rationales.

Experimental Results

The paper performs comprehensive evaluations using the GSM8K set for mathematical problem solving and the broader BIG-Bench Hard benchmark suite.

Performance Metrics: TRICE significantly outperforms baseline models including STaR and direct tuning, achieving higher accuracy in producing correct answers. This is validated through greedy decoding and self-consistency methods, where TRICE shows improvements in generating valid rationales across the board.

Advantages Over STaR: Compared to the STaR algorithm, TRICE avoids the pitfall of ignoring challenging examples, thus enhancing overall performance by being able to learn from both correct and incorrect rationales.

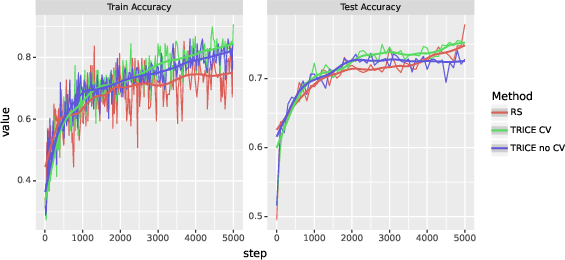
Figure 1: Time-varying estimates (with loess smoothers) of average training-set accuracy $p(y\mid x)$ and greedy-decoding validation-set accuracy for TRICE with and without the subsampled control-variate gradient estimator ("TRICE CV" and "TRICE no CV" respectively) and four-particle rejection sampling ("RS") on GSM8K.

Implications and Future Directions

The introduction of latent-variable inference through TRICE expands the landscape of CoT methods by demonstrating a feasible pathway to enhance LLM reasoning capabilities without extensive manual labeling. The probabilistic framework allows for a robust combination of reasoning paths at both training and inference stages, potentially leading to more nuanced model behaviors and applications.

Theoretical and Practical Impact: The method challenges the conventional reliance on direct supervision by showcasing the practical viability of latent-variable modeling. This has significant implications for developing models that generalize better across diversified reasoning tasks and benchmarks.

Prospects for Future Research: The paper paves the way for applying similar inference frameworks to other domains like tool-use, where reasoning processes are integral. Further exploration into optimizing the scalability and efficiency of such models across different architectures and task complexities remains an open frontier.

Conclusion

"Training Chain-of-Thought via Latent-Variable Inference" (2312.02179) presents a strategic advancement in reasoning with large models by leveraging latent-variable inference using TRICE. This method not only outperforms existing solutions but also sets the stage for future explorations in enhancing LLM capabilities via sophisticated probabilistic approaches to reasoning.