Multi-population Mean Field Games with Multiple Major Players: Application to Carbon Emission Regulations (2309.16477v1)

Abstract: In this paper, we propose and study a mean field game model with multiple populations of minor players and multiple major players, motivated by applications to the regulation of carbon emissions. Each population of minor players represent a large group of electricity producers and each major player represents a regulator. We first characterize the minor players equilibrium controls using forward-backward differential equations, and show existence and uniqueness of the minor players equilibrium. We then express the major players' equilibrium controls through analytical formulas given the other players' controls. Finally, we then provide a method to solve the Nash equilibrium between all the players, and we illustrate numerically the sensitivity of the model to its parameters.

• The paper presents a novel multi-population mean field game model that integrates multiple major regulators and minor electricity producers in carbon emission regulation.
• It employs forward-backward differential equations and a linear quadratic framework to derive equilibrium strategies for both minor and major players.
• Numerical experiments demonstrate how different carbon tax levels and network connectivity affect production levels across interacting populations.

Multi-population Mean Field Games with Multiple Major Players: Application to Carbon Emission Regulations

This essay analyzes the proposed mean field game (MFG) model in the paper titled "Multi-population Mean Field Games with Multiple Major Players: Application to Carbon Emission Regulations" (2309.16477). The model addresses regulation issues in carbon emissions by considering interactions between multiple populations of minor players and major players. This paper elucidates mathematical formulations and applications for modeling strategic decisions in carbon emissions regulations across different populations.

Mean Field Game Model

The proposed MFG model is designed to simulate large groups of electricity producers (minor players) interacting within multiple populations, overseen by regulators (major players). Each population represents a cohort of electricity producers, and each major player acts as a regulator implementing carbon emission policies. The model is founded on forward-backward differential equations to define equilibrium controls for minor players, asserting the existence and uniqueness of these controls. Major players establish their controls based on analytical solutions derived from the observed behaviors of other players in the game.

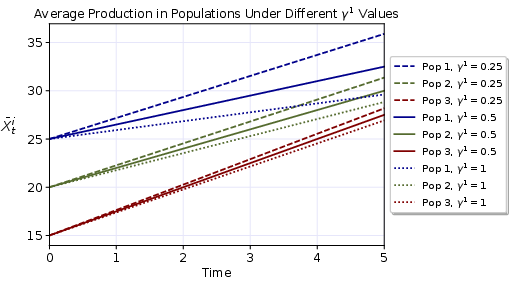
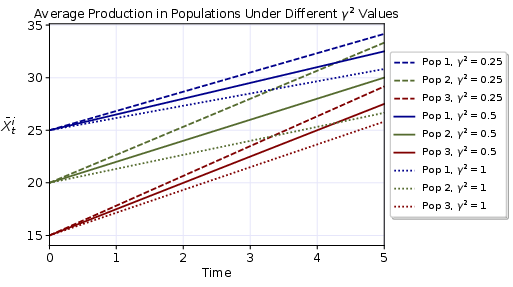
Figure 1: The effect of different carbon tax levels in population 1 (top) and in population 2 (bottom) on average production levels.

Mathematical Formulation

Minor Players' Control

The minor players' equilibrium is attained through solving a system of forward-backward stochastic differential equations (FBSDEs). The equilibrium requires each minor player's control to minimize their cost, which is computed as:

$$\hat{\alpha}^{i}_t = -\frac{\eta^i}{2 \gamma^i} Y^i_t,$$

where $Y^i_t$ is solved via FBSDEs.

To simplify computation, the linear quadratic structure allows reduction to an ordinary differential equation (ODE) system. This approach leverages the Pontryagin maximum principle for derivation.

Major Players' Control

The major players' equilibrium is crucially contingent on minimizing their carbon tax rates. The best response for the major player $i$ is formulated analytically considering the other major players' controls as follows:

${\gamma}^{i*} = \dfrac{\tau^i - 2\sum_{j=1, j\neq i}^{M}_{i,j}\gamma^j}{-2\kappa_g-2[i,:]\mathds{1}_M + 2[i,i]},$

yielding equilibrium solutions under the assumption of invertibility of specific matrices.

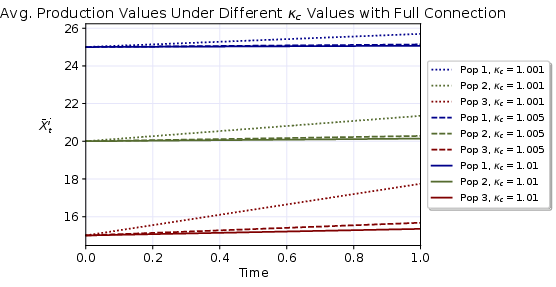
Figure 2: The effect of different coefficient of importance major players give to the cost of minor players in their population.

Numerical Experiments

The model is demonstrated numerically using simulations involving three populations and major players, with the interactions governed by either partial or full connectivity between the populations. These simulations reveal how variations in carbon tax levels and coefficients of net earnings impact production levels across interconnected populations.

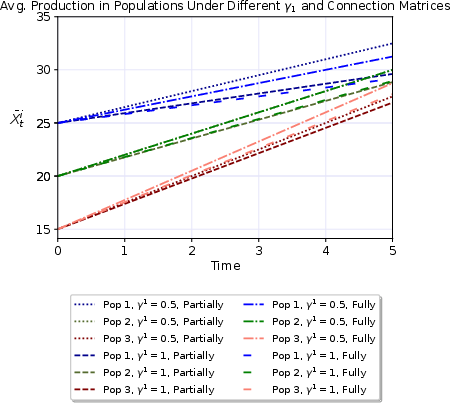
Figure 3: The effect of different carbon tax levels in population 1 with various connection setups between populations.

Overall, the numerical experiments illustrate sensitivity of production levels to regulatory parameters and demonstrate potential outcomes for regulatory strategies in multi-population settings.

Conclusions and Future Work

The paper extends the conventional applications of mean field games into the field of carbon emission regulations with a novel multi-population approach. It opens pathways for modeling strategic interactions among diverse player populations in other fields, like energy management and resource allocation.

Future work may encompass incorporating consumer populations, exploring more intricate network structures within populations, and performing large-scale simulations with complex interconnections and varying parameter values. Additionally, exploring Stackelberg equilibrium in these settings offers promising avenues for extending the theoretical framework to multi-population games.