What learning algorithm is in-context learning? Investigations with linear models (2211.15661v3)

Abstract: Neural sequence models, especially transformers, exhibit a remarkable capacity for in-context learning. They can construct new predictors from sequences of labeled examples $(x, f(x))$ presented in the input without further parameter updates. We investigate the hypothesis that transformer-based in-context learners implement standard learning algorithms implicitly, by encoding smaller models in their activations, and updating these implicit models as new examples appear in the context. Using linear regression as a prototypical problem, we offer three sources of evidence for this hypothesis. First, we prove by construction that transformers can implement learning algorithms for linear models based on gradient descent and closed-form ridge regression. Second, we show that trained in-context learners closely match the predictors computed by gradient descent, ridge regression, and exact least-squares regression, transitioning between different predictors as transformer depth and dataset noise vary, and converging to Bayesian estimators for large widths and depths. Third, we present preliminary evidence that in-context learners share algorithmic features with these predictors: learners' late layers non-linearly encode weight vectors and moment matrices. These results suggest that in-context learning is understandable in algorithmic terms, and that (at least in the linear case) learners may rediscover standard estimation algorithms. Code and reference implementations are released at https://github.com/ekinakyurek/google-research/blob/master/incontext.

• The paper demonstrates that transformers can implicitly execute learning algorithms, implementing steps akin to gradient descent and ridge regression.
• It uses theoretical proofs and empirical experiments on linear regression to reveal phase transitions from shallow, gradient descent-like behavior to deeper, Bayesian predictions.
• The study finds that hidden activations encode key quantities, such as moment matrices and weight vectors, highlighting interpretable algorithmic dynamics.

Linear Models and In-Context Learning

The paper "What learning algorithm is in-context learning? Investigations with linear models" (2211.15661) explores the hypothesis that in-context learning (ICL) in transformers can be understood as an implicit implementation of standard learning algorithms. Specifically, the authors investigate whether transformers encode smaller models within their activations and update these implicit models as new examples appear in the context. The paper uses linear regression as a prototypical problem and provides theoretical and empirical evidence to support this hypothesis.

Theoretical Implementation of Learning Algorithms

In Section 3, the paper demonstrates that transformers can theoretically implement learning algorithms for linear models. The authors prove, through constructive methods, that transformers can perform a single step of gradient descent with $\mathcal{O}(d)$ hidden size and constant depth. They also show that a transformer can update a ridge regression solution to include a new observation with $\mathcal{O}(d^2)$ hidden size and constant depth, where $d$ is the dimension of the linear regression problem. These results provide upper bounds on the capacity required to implement these algorithms.

Empirical Analysis of In-Context Learners

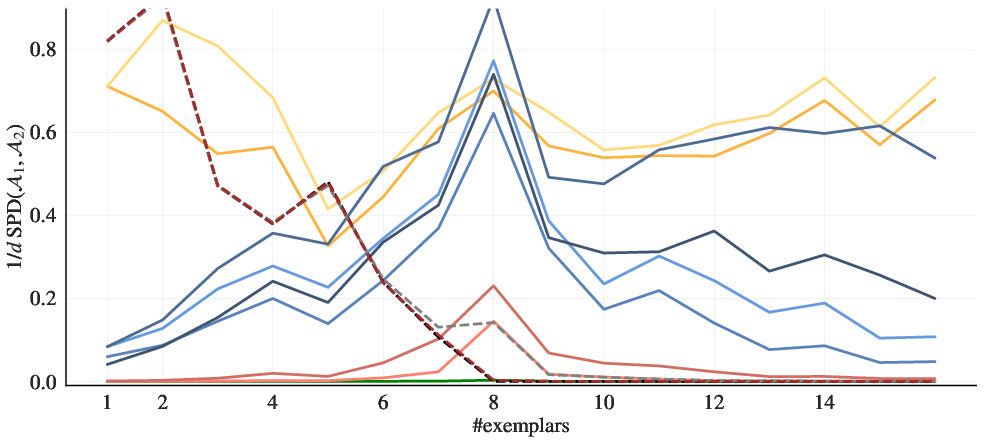
Figure 1: Predictor--ICL fit w.r.t. prediction differences.

Section 4 focuses on empirical properties of trained in-context learners. The authors construct linear regression problems where the learner's behavior is underdetermined by training data. They find that model predictions closely match existing predictors, such as gradient descent, ridge regression, and exact least-squares regression. The transition between different predictors varies with model depth and training set noise. Furthermore, at large hidden sizes and depths, the learners behave like Bayesian predictors. As shown in (Figure 1), the in-context learners exhibit close alignment with ordinary least squares, demonstrating a better approximation compared to alternative solutions for linear regression problems.

Algorithmic Features in In-Context Learners

Figure 2: ICL under uncertainty: With problem dimension $d=8$, and for different values of prior variance $\tau^2$ and data noise $\sigma^2$, we display (dimension-normalized) MSPD values for each predictor pair, where MSPD is the average SPD value over underdetermined region of the linear problem. Brightness is proportional with $\frac{1}{\text{MSPD}$.

Section 5 presents preliminary evidence that in-context learners share algorithmic features with known predictors. The paper reveals that essential intermediate quantities, such as parameter vectors and moment matrices, can be decoded from the hidden activations of in-context learners. This suggests that learners' late layers encode weight vectors and moment matrices non-linearly. As illustrated in (Figure 2), the in-context learner closely follows the minimum Bayes-risk Ridge regression output for all $\frac{\sigma^2}{\tau^2}$ values.

Computational Constraints and Phase Transitions

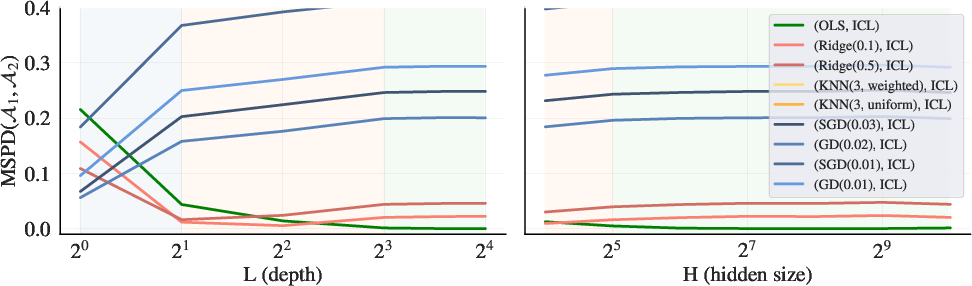
Figure 3: Linear regression problem with $d=8$

(Figure 3) presents a linear regression problem with $d=8$. As model depth increases, the in-context learners exhibit algorithmic phase transitions. Shallower models are better approximated by gradient descent, while deeper models align more closely with ridge regression and, eventually, ordinary least squares.

Probing for Intermediate Quantities

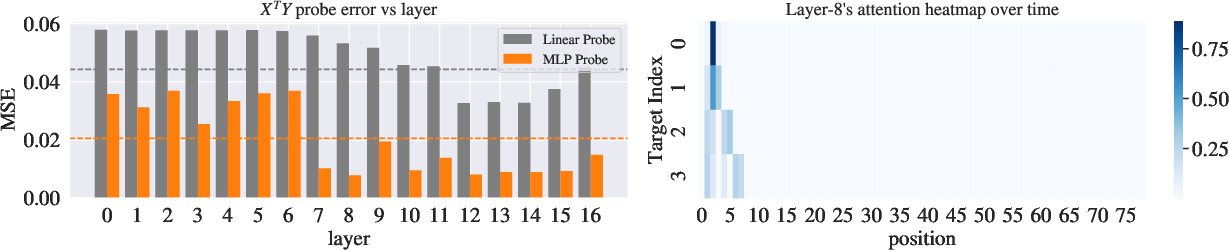
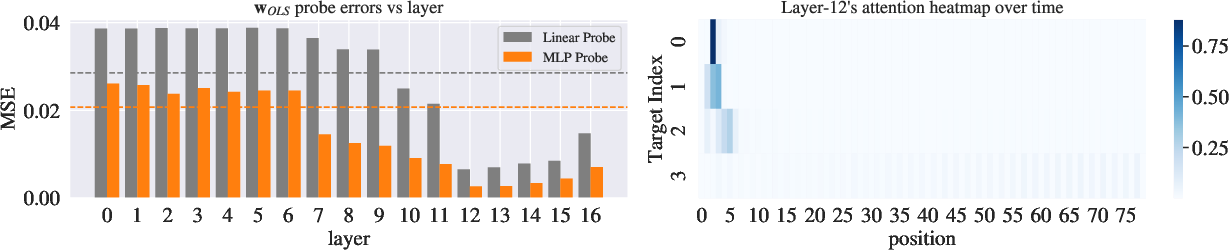
Figure 4: Probing results on $d=4$ problem: Both moments $X^\top Y$ (top) and least-square solution $_{\textrm{OLS}$ (middle) are recoverable from learner representations.

(Figure 4) illustrates the probing results on a $d=4$ problem, demonstrating that both moments $X^\top Y$ and the least-squares solution $_{\textrm{OLS}$ are recoverable from learner representations. Probing the in-context learners reveals that the moment vector $X^\top Y$ and the least-squares estimated weight vector can be decoded from the hidden representations. These targets are encoded nonlinearly and decoded accurately deep within the network.

Implications and Future Directions

This research suggests that in-context learning can be understood in algorithmic terms and that transformers may rediscover standard estimation algorithms. The findings open avenues for improving our understanding of the capabilities and limitations of deep networks. Future work could extend these experiments to richer function classes and larger-scale examples of ICL, such as LLMs, to determine whether their behaviors can also be described by interpretable learning algorithms.

Conclusion

The paper offers initial evidence that the phenomenon of in-context learning can be analyzed using standard ML tools and that solutions to learning problems discovered by machine learning researchers can also be discovered through sequence modeling tasks alone.