Dynamic Pricing for Non-fungible Resources: Designing Multidimensional Blockchain Fee Markets (2208.07919v2)

Abstract: Public blockchains implement a fee mechanism to allocate scarce computational resources across competing transactions. Most existing fee market designs utilize a joint, fungible unit of account (e.g., gas in Ethereum) to price otherwise non-fungible resources such as bandwidth, computation, and storage, by hardcoding their relative prices. Fixing the relative price of each resource in this way inhibits granular price discovery, limiting scalability and opening up the possibility of denial-of-service attacks. As a result, many prominent networks such as Ethereum and Solana have proposed multi-dimensional fee markets. In this paper, we provide a principled way to design fee markets that efficiently price multiple non-fungible resources. Starting from a loss function specified by the network designer, we show how to compute dynamic prices that align the network's incentives (to minimize the loss) with those of the users and miners (to maximize their welfare), even as demand for these resources changes. Our pricing mechanism follows from a natural decomposition of the network designer's problem into two parts that are related to each other via the resource prices. These results can be used to efficiently set fees in order to improve network performance.

• The paper introduces a multidimensional pricing mechanism that separates blockchain resources to align network usage with user and miner incentives.
• It employs a gradient-based optimization approach to adjust prices dynamically based on resource utilization deviations from target vectors.
• Simulations reveal that multidimensional pricing improves transaction throughput and balances resource allocation under network stress.

Dynamic Pricing for Non-fungible Resources: Designing Multidimensional Blockchain Fee Markets

Introduction

The paper examines fee market structures in public blockchains, focusing on how a multidimensional pricing strategy could enhance the allocation efficiency of non-fungible resources. Current blockchain fee models, like those on Ethereum, use gas as a unified metric to price resources such as computation and storage, which leads to inefficiencies and potential vulnerabilities such as denial-of-service (DoS) attacks. The paper proposes an adaptive pricing mechanism that separately evaluates distinct blockchain resources to align network usage intentions with the user and miner incentives.

Multidimensional Fee Market Design

The core proposal is a fee market design that dynamically adjusts resource prices based on demand, using a loss function set by the network designer to mediate between network efficiency and user incentives. The loss function quantifies the network's dissatisfaction based on resource utilization deviations from predefined targets. The authors present a mechanism that updates prices by decomposing the network optimization problem into two linked subproblems solved separately by the network and transaction producers.

For instance, given a target resource utilization vector $b^\star$, the network adjusts the prices, increasing them for over-utilized resources and decreasing for under-utilized ones, to steer demand closer to $b^\star$. The adaptation rule for price updates uses gradient-based methods derived from the network designer's optimization scenario, favoring a balance between computational feasibility and optimal price discovery.

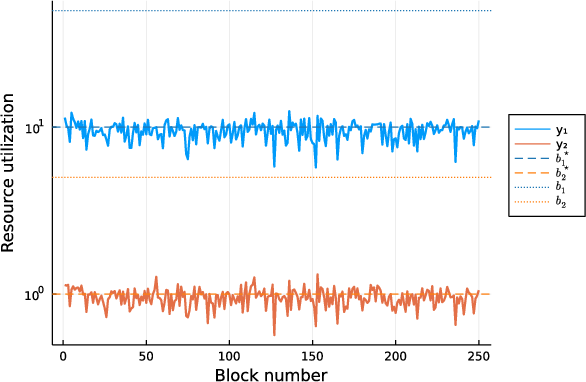
Figure 1: Resource utilization for multidimensional pricing (left) clusters closer to target values than for uniform pricing (right), which includes limited information about individual targets or caps.

Implementation and Algorithmic Considerations

The implementation of the proposed pricing mechanism relies on efficiently solving the dual optimization problem of dynamically orchestrating resource prices. This involves solving a convex optimization problem via projected gradient descent. The transactions' resource consumption data, along with the targets, feed into a model that iteratively evaluates the discrepancy in resource usage against set targets, subsequently refining resource prices.

Through analytical exploration, the paper outlines scenarios where separation of resource prices can lead to significant performance gains, especially under network stress or sudden shifts in transaction types.

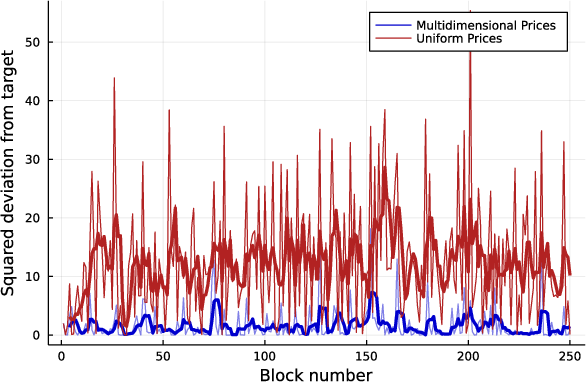
Figure 2: Squared deviation from the target values given by $b^\star$ in resource 1 utilization (left) and resource 2 utilization (right) for both uniform and multidimensional pricing. The thicker line is the four-sample moving average.

Experimental Evaluation

In realistic simulations, multidimensional pricing models exhibited a propensity for more balanced resource allocation, accommodating resource-hogging transactions more justly by avoiding systemic saturation. By maintaining individually assessed price points for each type of resource, the network was seen to achieve higher transaction throughput, optimizing for long-term node performance without imposing excessive hardware demands on participants.

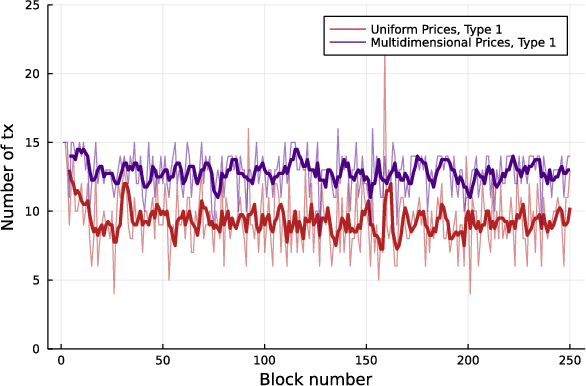
Figure 3: Multidimensional pricing allows us to include more transactions per block (left) by optimally adjusting prices (right). The thicker line is the four-sample moving average of the data.

Practical Implications and Future Directions

The proposed solution hints at improved resilience against strategic behaviors from transaction producers who might exploit static pricing strategies. Furthermore, this approach opens avenues for adopting similar models in other blockchain configurations, especially where congestion and transaction complexity vary widely.

Future studies could extend to detailed game-theoretic evaluations, exploring strategic behaviors from complex network participants and potential edge cases impacting the suggested pricing dynamics. Additionally, thorough empirical testing on testnets and adaptive simulation environments will be crucial to validate and iterate the multidimensional pricing strategy's viability in production settings.

Conclusion

The research provides a structured approach to resource pricing in blockchain environments, demonstrating how multidimensional fee markets could lead to enhanced equilibrium in resource utilization, ultimately fostering a more scalable and robust blockchain system. Through thoughtful design and implementation, this work advances existing methodologies to address systemic limitations determined by overly simplistic resource pricing structures.