Generalized Variational Continual Learning

Abstract: Continual learning deals with training models on new tasks and datasets in an online fashion. One strand of research has used probabilistic regularization for continual learning, with two of the main approaches in this vein being Online Elastic Weight Consolidation (Online EWC) and Variational Continual Learning (VCL). VCL employs variational inference, which in other settings has been improved empirically by applying likelihood-tempering. We show that applying this modification to VCL recovers Online EWC as a limiting case, allowing for interpolation between the two approaches. We term the general algorithm Generalized VCL (GVCL). In order to mitigate the observed overpruning effect of VI, we take inspiration from a common multi-task architecture, neural networks with task-specific FiLM layers, and find that this addition leads to significant performance gains, specifically for variational methods. In the small-data regime, GVCL strongly outperforms existing baselines. In larger datasets, GVCL with FiLM layers outperforms or is competitive with existing baselines in terms of accuracy, whilst also providing significantly better calibration.

• The paper presents GVCL, which unifies Variational Continual Learning and Online EWC by using a tunable β parameter in a likelihood-tempered framework.
• It employs likelihood-tempered variational inference to balance prediction accuracy with adherence to prior distributions, effectively adapting to various task demands.
• FiLM layers are integrated to mitigate overpruning, enhancing feature utilization and yielding superior performance across multiple benchmarks.

Generalized Variational Continual Learning

The paper "Generalized Variational Continual Learning" presents a novel approach to continual learning (CL) through the introduction of Generalized Variational Continual Learning (GVCL). This approach builds on existing methods such as Variational Continual Learning (VCL) and Online Elastic Weight Consolidation (Online EWC), uniting them under a single framework. The paper further incorporates FiLM layers to mitigate issues associated with overpruning, a significant challenge in variational inference (VI) settings.

Likelihood-Tempered Variational Inference

GVCL introduces likelihood-tempering to VCL, thereby bridging the gap between VCL and Online EWC. This method involves adjusting the KL-divergence regularization term by a factor $\beta$, effectively interpolating between VCL ($\beta=1$) and Online EWC ($\beta \to 0$). The resulting $\beta$-ELBO balances prediction accuracy with adherence to prior distributions, offering a tunable range that captures both local and global parameter structures based on the choice of $\beta$.

Special Case Analysis: Online EWC from GVCL

GVCL demonstrates that Online EWC is a limiting case of their framework by setting $\beta \to 0$. This insight reveals that GVCL not only subsumes VCL and Online EWC but also provides a continuum that can be adapted based on task characteristics and desired regularization strength. The derivation showcases how the curvature of the posterior can be adjusted dynamically, offering a more robust method for CL.

FiLM Layers as Architectural Modifications

The introduction of FiLM layers in conjunction with GVCL addresses the problem of overpruning. In variational methods, weights may return to their prior distribution to minimize the KL divergence, inadvertently shutting down network nodes due to biased initialization. FiLM layers introduce task-specific linear modulations that enhance feature utilization across tasks without incurring additional distributional treatment or regularization penalties. This modification is shown to increase the number of active units significantly (Figure 1).

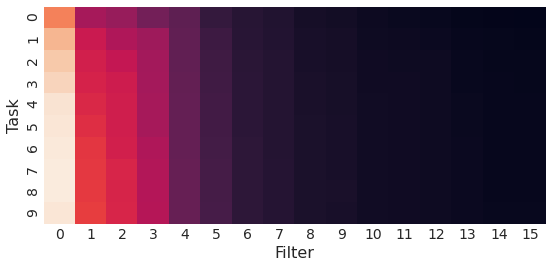
Figure 1: Visualizations of deviation from the prior distribution for filters in the first layer of a convolutional network trained on Hard-CHASY, demonstrating increased active units with FiLM layers.

Experimental Evaluation

The efficacy of GVCL combined with FiLM layers is tested across various benchmarks such as CHASY, Split-MNIST, Split-CIFAR, and Mixed Vision Tasks. The evaluations confirm the superior performance of GVCL-F over state-of-the-art methods, with significant gains in accuracy, forward transfer, and error calibration.

Performance Metrics and Results

GVCL-F consistently outperformed baselines in environments with complex, multi-domain task sequences. Tests on Split-CIFAR and Mixed Vision Tasks highlighted GVCL-F's strengths in managing task-specific feature extraction and maintaining robust performance through a Bayesian calibration framework (Figure 2).

Figure 2: Running average accuracy of GVCL-F on Split-CIFAR compared against baselines, demonstrating superior forward transfer.

Implications and Future Work

The unification of VCL and Online EWC through GVCL provides a flexible and encompassing framework that can be tailored to specific CL scenarios. The integration of FiLM layers not only resolves the overpruning issue but also leverages task-specific adaptations to optimize learning efficiency and network capacity. Future research directions include integrating GVCL with memory replay systems and exploring unsupervised task identification mechanisms to further enhance autonomous CL.

Conclusion

In summary, the paper presents GVCL as a comprehensive generalization of variational methods for CL, effectively merging distinct paradigms to exploit their collective strengths. By combining GVCL with FiLM layers, the approach substantiates significant improvements over traditional baselines concerning accuracy, transferability, and model calibration, marking a step forward in the practical application of continual learning frameworks.