Grid-Based Stochastic Model Predictive Control for Trajectory Planning in Uncertain Environments (2007.12430v3)

Abstract: Stochastic Model Predictive Control has proved to be an efficient method to plan trajectories in uncertain environments, e.g., for autonomous vehicles. Chance constraints ensure that the probability of collision is bounded by a predefined risk parameter. However, considering chance constraints in an optimization problem can be challenging and computationally demanding. In this paper, we present a grid-based Stochastic Model Predictive Control approach. This approach allows to determine a simple deterministic reformulation of the chance constraints and reduces the computational effort, while considering the stochastic nature of the environment. Within the proposed method, we first divide the environment into a grid and, for each predicted step, assign each cell a probability value, which represents the probability that this cell will be occupied by surrounding vehicles. Then, the probabilistic grid is transformed into a binary grid of admissible and inadmissible cells by applying a threshold, representing a risk parameter. Only cells with an occupancy probability lower than the threshold are admissible for the controlled vehicle. Given the admissible cells, a convex hull is generated, which can then be used for trajectory planning. Simulations of an autonomous driving highway scenario show the benefits of the proposed grid-based Stochastic Model Predictive Control method.

• The paper introduces a grid-based SMPC framework that converts probabilistic chance constraints into deterministic ones via a binary grid transformation.
• It employs convex hull techniques to simplify the optimization process, enabling efficient real-time trajectory planning even during complex maneuvers like overtaking.
• Simulation results validate the approach's scalability and computational efficiency, ensuring robust collision-free navigation in dynamic environments.

Grid-Based Stochastic Model Predictive Control for Trajectory Planning in Uncertain Environments

Introduction

The paper discusses the implementation and application of a grid-based Stochastic Model Predictive Control (SMPC) approach for trajectory planning within uncertain environments, particularly focused on autonomous driving scenarios. The approach innovatively utilizes a probabilistic grid to address the computational challenges associated with chance constraints intrinsic to SMPC, thereby allowing efficient trajectory planning that accounts for stochastic vehicle behavior.

Methodology

Probabilistic Occupancy Grid

The environment is discretized into a grid where each cell is assigned an occupancy probability, representing the likelihood of that cell being occupied by a surrounding vehicle at any future prediction step. This probabilistic occupancy grid, or probabilistic grid, is critical for defining the space constraints of the ego vehicle (EV). Unlike traditional methods that rely on Gaussian assumptions for simplicity, this method supports arbitrary probability distributions, thereby enhancing flexibility in various driving contexts.

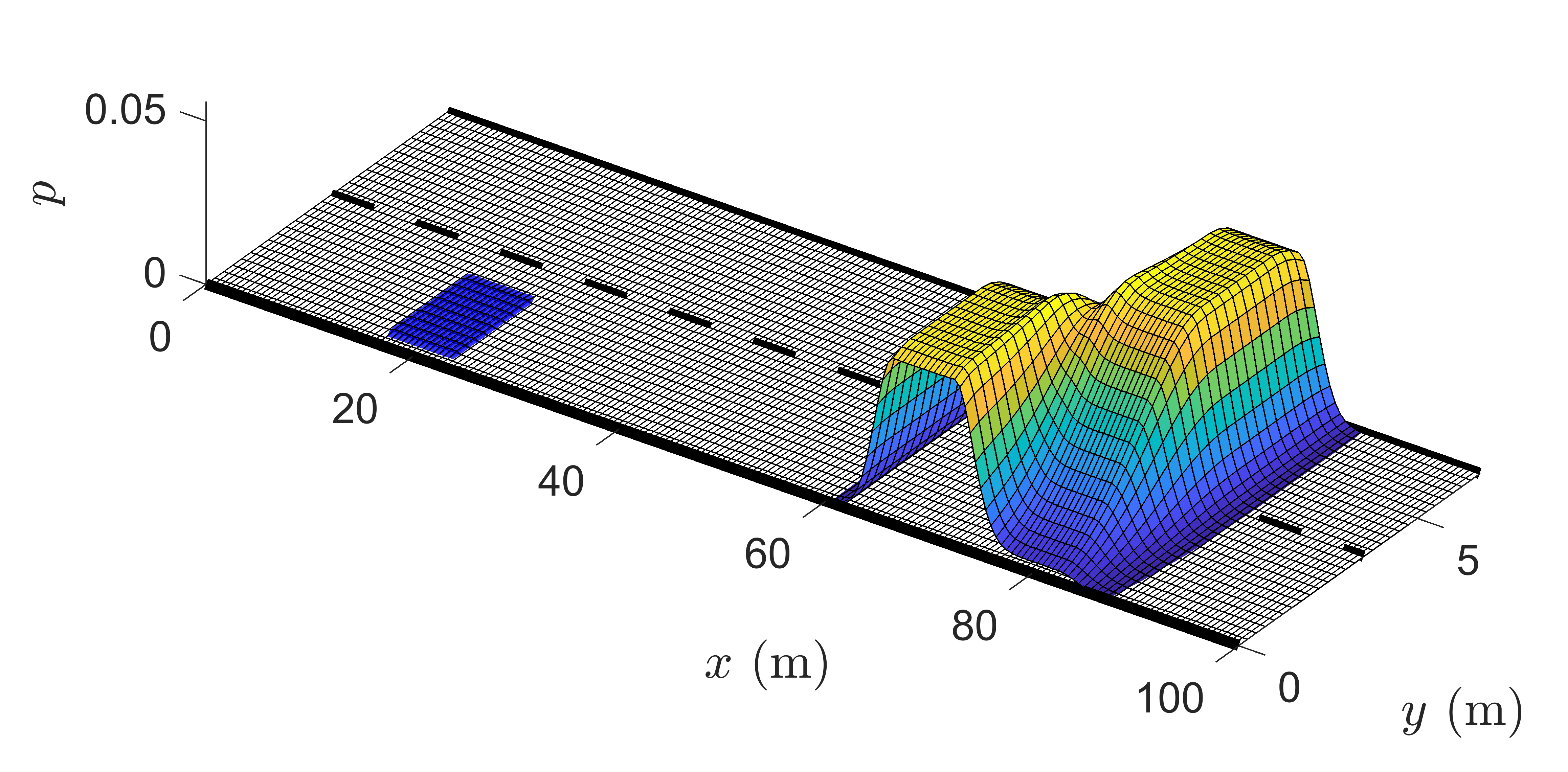
Figure 1: Probabilistic Grid of a prediction step. The EV is on the left in blue and multiple TVs are displayed on the right.

Binary Grid Transformation

To reformulate the probabilistic chance constraints into deterministic constraints feasible within an optimization framework, the probabilistic grid is converted into a binary grid. This transformation is achieved by imposing a threshold on the occupancy probabilities, thus distinguishing admissible regions from inadmissible ones for EV navigation. The result is a binary matrix that enables efficient constraint definition in a convex optimization problem.

Convex Hull and Optimization Problem

The admissible areas derived from the binary grid are used to create a convex hull, which further describes the constraints in linear inequality form, suitable for inclusion within an optimization problem. This convex representation simplifies the constraint handling within the model predictive control framework. Moreover, the optimization problem is solved iteratively to determine the optimal control inputs for the EV, achieving safe and efficient trajectory planning even in dynamically changing traffic scenarios.

Simulation Results

Overtaking Scenario

The paper presents a simulation where the SMPC method is applied to an overtaking maneuver on a highway scenario involving multiple target vehicles (TVs). The simulation effectively demonstrates the method’s capacity to ensure collision-free navigation by the EV, which adapts by executing lane changes and overtakes based on the probabilistic assessments of the surrounding TVs’ trajectories.

Computational Efficiency

The method's computational efficiency is also validated through tests with varying numbers of target vehicles, showing that the grid-based SMPC approach maintains consistent computational demands irrespective of the number of TVs considered. This is pivotal for real-time applications where computational resources are a constraint.

Discussion and Future Implications

The presented grid-based approach effectively reduces the conservatism associated with traditional robust planning methods while maintaining safe navigation through probabilistic assessments. A significant implication of this research is its scalability; the method can accommodate increases in the number of dynamic obstacles without significant computational overhead, a factor crucial for urban autonomous driving scenarios. Furthermore, future work might investigate the integration of this method with more complex 3D environments or the development of adaptive mechanisms for threshold determination to enhance robustness across varied operating conditions.

Conclusion

The grid-based SMPC methodology offers a practical and computationally efficient solution for trajectory planning in uncertain environments, with direct applications in autonomous driving. It enables the incorporation of complex probability distributions within a manageable optimization framework, facilitating safer and more reliable autonomous system operation amidst the challenges posed by dynamic and uncertain real-world conditions. The method’s scalability and adaptability suggest promising applications beyond current use cases, potentially extending into robotics and other domains requiring sophisticated trajectory planning capabilities.