Meta-learning curiosity algorithms

Abstract: We hypothesize that curiosity is a mechanism found by evolution that encourages meaningful exploration early in an agent's life in order to expose it to experiences that enable it to obtain high rewards over the course of its lifetime. We formulate the problem of generating curious behavior as one of meta-learning: an outer loop will search over a space of curiosity mechanisms that dynamically adapt the agent's reward signal, and an inner loop will perform standard reinforcement learning using the adapted reward signal. However, current meta-RL methods based on transferring neural network weights have only generalized between very similar tasks. To broaden the generalization, we instead propose to meta-learn algorithms: pieces of code similar to those designed by humans in ML papers. Our rich language of programs combines neural networks with other building blocks such as buffers, nearest-neighbor modules and custom loss functions. We demonstrate the effectiveness of the approach empirically, finding two novel curiosity algorithms that perform on par or better than human-designed published curiosity algorithms in domains as disparate as grid navigation with image inputs, acrobot, lunar lander, ant and hopper.

• The paper presents a dual-loop meta-learning framework that evolves curiosity algorithms, efficiently boosting exploration in diverse reinforcement learning environments.
• The methodology integrates intrinsic reward computation and reward combining via a domain-specific language to explore a combinatorial search space.
• Empirical results reveal strong correlations between performance in simple and complex tasks, demonstrating the generality and efficiency of the meta-learned algorithms.

Meta-Learning Curiosity Algorithms

Introduction

The paper "Meta-learning curiosity algorithms" (2003.05325) introduces an innovative approach to enhance the exploration capabilities of reinforcement learning (RL) agents by leveraging the concept of curiosity. By formulating the problem as one of meta-learning, the authors propose a dual-loop method: an outer evolutionary-scale loop that searches through a space of curiosity-inducing algorithms, and an inner loop that applies standard RL techniques with modified reward signals. This perspective aims to automate the discovery of curiosity mechanisms that can generalize across diverse environments, contrasting with traditional hand-crafted strategies typically limited to specific domains.

Methodology

The core of this research lies in utilizing a meta-learning framework to evolve curiosity algorithms. Each candidate algorithm modifies the agent's reward signal to encourage exploratory behaviors that lead to long-term reward maximization. The approach diverges from existing meta-RL methods by focusing on meta-learning of algorithmic structures, rather than the weights of neural networks, thereby enabling broader generalization across dissimilar tasks.

The intrinsic curiosity modules generated comprise two components:

• Intrinsic Reward Component (I): Computes intrinsic rewards based on state transitions.
• Reward Combiner ($\chi$): Integrates intrinsic and extrinsic rewards to produce a proxy reward.

These components utilize a domain-specific programming language that includes neural network modules, gradient descent operations, buffers, and other functional elements that collectively form a combinatorial search space.

Figure 1: Example diagrams of published algorithms covered by our language (larger figures in the appendix). The green box represents the output of the intrinsic curiosity function, the pink box is the loss to be minimized. Pink arcs represent paths and networks along which gradients flow back from the minimizer to update parameters.

Empirical Results

Empirical validation demonstrates the approach's efficacy, revealing discovery of novel curiosity algorithms that outperform or match hand-designed algorithms across varied environments such as grid navigation, lunar lander, acrobot, ant, and hopper tasks. A notable finding is the "Fast Action-Space Transition" (FAST) program, which efficiently drives exploration by rewarding significant transitions between predicted and actual actions.

Figure 2: Correlation between program performance in gridworld and in harder environments (lunar lander on the left, acrobot on the right), using the top 2,000 programs in gridworld. Performance is evaluated using mean reward across all learning episodes, averaged over trials.

One key result is the strong correlation between algorithm performance in simpler environments (such as gridworld) and more complex environments (like acrobot and lunar lander), substantiating the generality of the meta-learned curiosity mechanisms.

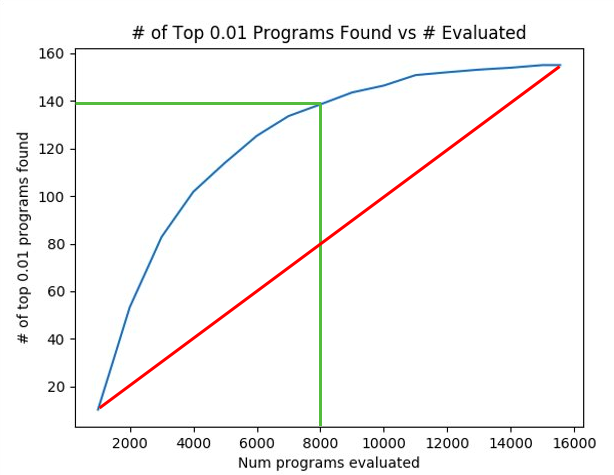
Figure 3: Predicting algorithm performance allows us to find the best programs faster. We investigate the number of the top 1% of programs found vs. the number of programs evaluated, and observe that the optimized search (in blue) finds 88% of the best programs after only evaluating 50% of the programs.

Implications and Future Work

The meta-learning approach to curiosity presents substantial implications for both theoretical exploration strategies and practical implementations in AI systems. By automating the search for exploratory behaviors, this method holds promise in scaling RL to more complex, high-dimensional spaces where manual design is ineffectual.

Future developments may explore extending the program search space, integrating additional environment types to foster even richer generalization, and hybridizing this meta-learning of algorithms with weight-based adaptation for enhanced performance in stable domains. Potential applications span across robotics, game playing, and autonomous navigation, where exploration efficiency is paramount.

Conclusion

This paper articulates a transformative approach to discover curiosity-driven strategies through meta-learning of algorithmic structures. By transcending the limitations of task-specific designs, it opens avenues for broader, more robust application of intrinsic motivation in reinforcement learning, enhancing our understanding and integration of curiosity in AI.