Scalable Second Order Optimization for Deep Learning

Abstract: Optimization in machine learning, both theoretical and applied, is presently dominated by first-order gradient methods such as stochastic gradient descent. Second-order optimization methods, that involve second derivatives and/or second order statistics of the data, are far less prevalent despite strong theoretical properties, due to their prohibitive computation, memory and communication costs. In an attempt to bridge this gap between theoretical and practical optimization, we present a scalable implementation of a second-order preconditioned method (concretely, a variant of full-matrix Adagrad), that along with several critical algorithmic and numerical improvements, provides significant convergence and wall-clock time improvements compared to conventional first-order methods on state-of-the-art deep models. Our novel design effectively utilizes the prevalent heterogeneous hardware architecture for training deep models, consisting of a multicore CPU coupled with multiple accelerator units. We demonstrate superior performance compared to state-of-the-art on very large learning tasks such as machine translation with Transformers, language modeling with BERT, click-through rate prediction on Criteo, and image classification on ImageNet with ResNet-50.

• The paper presents a scalable second-order optimization technique that reduces convergence steps by up to 50% using an optimized variant of full-matrix AdaGrad.
• It introduces asynchronous preconditioner computations to decouple costly matrix operations, resulting in significant wall-time reductions in training deep models.
• The method effectively leverages heterogeneous hardware, including CPUs, GPUs, and TPUs, to address computational and memory challenges in large-scale deep learning.

Scalable Second Order Optimization for Deep Learning

The paper "Scalable Second Order Optimization for Deep Learning" (2002.09018) explores the implementation of a second-order optimization technique, specifically a variant of full-matrix AdaGrad, to address the limitations of first-order methods in training large-scale deep learning models. The study engages with the fundamental challenges of computational and memory costs associated with second-order methods and presents systematic solutions for real-world applications on heterogeneous hardware architectures.

Introduction to Second Order Methods

Second-order optimization methods are theoretically advantageous due to their ability to exploit curvature information via second derivatives. These methods, however, have considerably higher computational and memory costs compared to first-order methods like SGD and Adam. The prohibitive cost often impedes their application to large-scale deep learning. The study addresses this gap by presenting an optimized implementation of a second-order method, Shampoo, that is adaptable to modern hardware, specifically relying on GPUs and TPUs coupled with CPUs for computational distribution.

Optimization Algorithm Design

The central contribution lies in the practical implementation of a second-order preconditioned algorithm on CPU-accelerated systems (Figure 1). Shampoo utilizes preconditioners derived from second-order statistics to provide superior convergence and runtime improvements in comparison with state-of-the-art first-order methods.

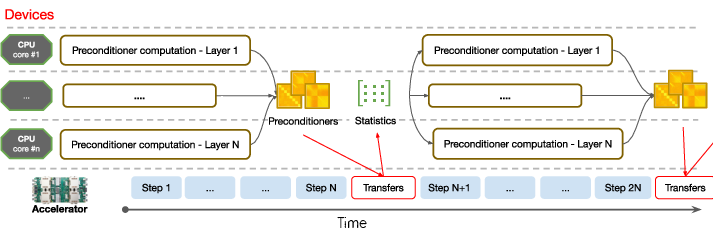
Figure 1: Timeline illustrating the design of the optimization algorithm. Preconditioner statistics (L_t and R_t) are computed at each step by the accelerators. Preconditioners ($L_t^{-\frac{1}{2p}}$ and $R_t^{-\frac{1}{2q}}$) are computed asynchronously every few steps.

Scalability and Real-World Implementation

The authors have introduced various improvements and novel strategies to ensure the scalability of the proposed method:

• Efficient Use of Hardware: The method leverages the multicore architecture of CPUs for computationally intensive preconditioner calculations while asynchronously pipelining these with GPU/TPU training operations.
• Preconditioner Frequency and Warm Start: Computation of preconditioners is decoupled from every optimization step, computed every few hundred steps, drastically minimizing real-time inefficiencies.
• Numerical Stability: The paper optimizes the use of iterative methods for matrix operations to handle the ill-conditioned nature of matrices typical in deep networks effectively.

Performance and Application

The performance of the proposed algorithm is evaluated across several large-scale tasks: machine translation with Transformers, language modeling with BERT, click-through rate prediction on the Criteo dataset, and image classification on ImageNet with ResNet-50. Key findings include:

• Significant Reduction in Steps: The algorithm demonstrated a reduction of up to 50% in the number of steps required to achieve benchmarks set by first-order methods, with only a marginal increase in per-step computation time.
• Wall-Time Improvements: The effective use of asynchronous preconditioner computations enabled a notable reduction in training wall-time, showcasing a decrease from 12 hours to 6.7 hours for the Transformer model on the WMT'14 dataset.

  Figure 2: Minimum (dashed) and maximum (solid) singular values for statistics matrices of the embedding, softmax, and intermediate attention query projection layers.

Conclusion and Future Implications

The study successfully demonstrates the viability of second-order optimization methods on large-scale architectures, indicating significant reduction in convergence time and resource utilization when compared to leading first-order methods. The approach prompts advancements in hardware support for precise arithmetic and memory operations crucial for scalable implementations of complex optimization algorithms within deep learning frameworks. Further integration and enhancement could support even larger models and foster innovation in both software and hardware design considerations for AI research.

This work provides a compelling case for broader adoption of second-order methods in AI, as the field continues to grapple with increasing scale and complexity constraints in model training and deployment.