- The paper introduces out-of-time-order correlations (OTOC) as a novel tool for detecting phase transitions in Floquet-driven Ising spin systems.
- It utilizes analytical techniques, including the Jordan-Wigner transformation, to derive precise solutions for transverse and longitudinal magnetization OTOCs.
- The findings reveal distinct phase boundaries in periodically driven systems, underscoring the method's potential in quantum simulation applications.
Out-of-Time-Order Correlation and Detection of Phase Structure in Floquet Transverse Ising Spin System
Introduction
The paper addresses the utilization of out-of-time-order correlations (OTOC) within the context of Floquet transverse Ising spin systems to discern the phase structure of such systems. OTOCs have garnered significant attention for their roles in quantum chaotic systems, quantum information scrambling, and phase detection in quantum critical systems. This framework provides insights into the behavior of dynamical quantum phase transitions, specifically within periodically driven systems.
Model Description
The authors investigate an integrable Floquet transverse Ising system characterized by binary Floquet drives. The Floquet map is given by:
$U = e^{-iH_{xx}\tau_{1}e^{-iH_{z}\tau_{0}$
where Hxx represents nearest neighbor Ising interaction and Hz signifies a transverse field. These components are pivotal in capturing the interplay between evolving quantum states and external driving forces.
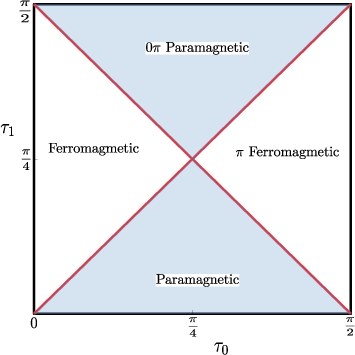
Figure 1: Phase structure of the Floquet system with Floquet map given by \cref{U_f.
Analytical Solutions for OTOCs
Transverse Magnetization OTOC (TMOTOC)
Using the Jordan-Wigner transformation, an exact analytical solution for the transverse magnetization OTOC is derived. This transformation maps spin operators onto fermionic operators, enabling the calculation of correlation propagation speed and revival time behavior. The TMOTOC formula conveys how correlations in transverse magnetization evolve over time, offering a basis for comparison with longitudinal magnetization.
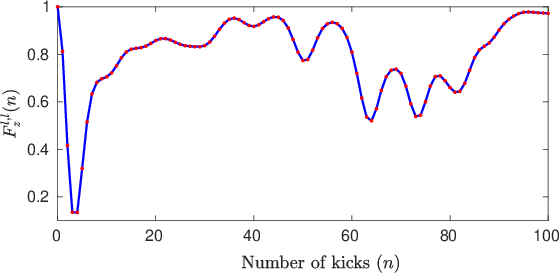
Figure 2: F<sup>l,l,</sup>demonstratingspreadingacrossvariousseparations.</p></p><h4class=′paper−heading′id=′longitudinal−magnetization−otoc−lmotoc′>LongitudinalMagnetizationOTOC(LMOTOC)</h4><p>TheLMOTOCservesasacrucialdiagnostictoolforidentifyingquantumphasetransitions.UnlikeTMOTOCs,LMOTOCsinferromagneticandparamagneticregimesshowdistinctlong−timeaveragebehaviors,permittingtheseregionstobeclassifiedusingaveragevaluesofLMOTOCasanorderparameter.<imgsrc="https://emergentmind−storage−cdn−c7atfsgud9cecchk.z01.azurefd.net/paper−images/2002−05986/otoczbutterrevivaln12.png"alt="Figure3"title=""class="markdown−image"loading="lazy"></p><p><imgsrc="https://emergentmind−storage−cdn−c7atfsgud9cecchk.z01.azurefd.net/paper−images/2002−05986/otocxbutterrevivaln12.png"alt="Figure3"title=""class="markdown−image"loading="lazy"><pclass="figure−caption">Figure3:Behaviourof(a)F_z^{l,m}incomparisonto(b)F_x^{l,m}overarangeofkicks.</p></p><h3class=′paper−heading′id=′phase−structure−analysis′>PhaseStructureAnalysis</h3><p>ThepaperbuildsupontheseOTOCstoexplorephasestructuresinherentinFloquetsystems.Notably,thephasediagramsrevealfourdistinctregimes,incorporatingbothconventionalandFloquet−specificphasessuchas\pi−ferromagneticand0\pi−paramagnetic.Thesharpnessofphaseboundariesareattributedtosymmetry−protectedIsingorderdynamics.<imgsrc="https://emergentmind−storage−cdn−c7atfsgud9cecchk.z01.azurefd.net/paper−images/2002−05986/otoczn12tau0pi28.png"alt="Figure4"title=""class="markdown−image"loading="lazy"></p><p><imgsrc="https://emergentmind−storage−cdn−c7atfsgud9cecchk.z01.azurefd.net/paper−images/2002−05986/otocxn12tau0pi28.png"alt="Figure4"title=""class="markdown−image"loading="lazy"><pclass="figure−caption">Figure4:(a)VariationofF_x^{l,l}$ under varying conditions showing alignment with theoretical expectations.
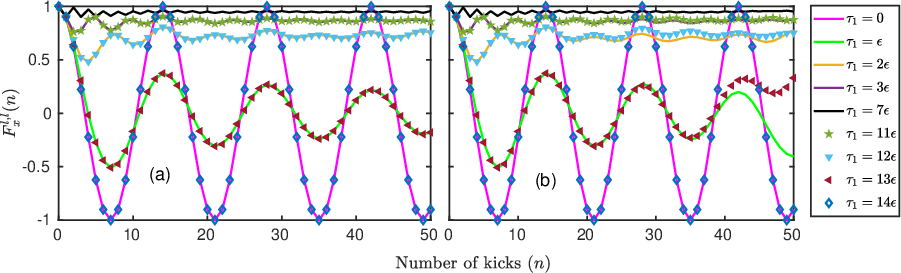
Figure 5: Variation of critical points with respect to finite and infinite size systems.
Conclusion
By presenting exact analytical solutions alongside numerical validations, the paper underscores the effectiveness of OTOCs in evaluating phase transitions in Floquet systems. Discoveries of nontrivial phase structures accentuate the potential for experimental realizations, further leveraging tools such as LMOTOC for phase structure identification in driven quantum systems.
Experimental and computational techniques, facilitated by the manipulation and measurement of OTOCs, provide avenues for practical applications in quantum simulations and phase transition analysis within modern quantum technologies.


