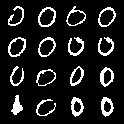Papers
Topics
Authors
Recent
Search
2000 character limit reached

Categorical Flow Maps

Published 12 Feb 2026 in cs.LG | (2602.12233v1)

Abstract: We introduce Categorical Flow Maps, a flow-matching method for accelerated few-step generation of categorical data via self-distillation. Building on recent variational formulations of flow matching and the broader trend towards accelerated inference in diffusion and flow-based models, we define a flow map towards the simplex that transports probability mass toward a predicted endpoint, yielding a parametrisation that naturally constrains model predictions. Since our trajectories are continuous rather than discrete, Categorical Flow Maps can be trained with existing distillation techniques, as well as a new objective based on endpoint consistency. This continuous formulation also automatically unlocks test-time inference: we can directly reuse existing guidance and reweighting techniques in the categorical setting to steer sampling toward downstream objectives. Empirically, we achieve state-of-the-art few-step results on images, molecular graphs, and text, with strong performance even in single-step generation.

Summary

  • The paper presents a novel framework that accelerates discrete generation by defining a continuous flow on the probability simplex for high-quality few-step sampling.
  • It leverages self-distillation and endpoint parametrization to ensure numerical stability and geometric consistency while constraining predictions to valid categorical distributions.
  • Empirical results across molecular graphs, images, and text demonstrate significant reductions in NFEs, outperforming baselines in speed and sample accuracy.

Categorical Flow Maps: Accelerated Few-Step Generation for Discrete Data

Introduction and Motivation

Categorical Flow Maps (CFMs) (2602.12233) address the bottleneck of slow inference in discrete diffusion models, particularly for categorical domains such as text, molecular graphs, and images. Traditional discrete diffusion methods, while closing the quality gap with autoregressive baselines, require many function evaluations (NFEs), often resembling permuted autoregressive generators at test time. In contrast, fast consistency models in the continuous domain have demonstrated that careful training with self-distillation allows comparable or superior sample quality in just a few steps. The challenge in porting such acceleration to discrete data arises from the stochastic nature of Markov chain-based interpolations, which precludes direct application of continuous consistency objectives.

CFMs provide a solution by defining a continuous flow-based generative process on the probability simplex, interpolating from a continuous prior at the origin to an atomic (discrete) data distribution at the endpoint. This framework enables compatibility with state-of-the-art self-distillation and consistency techniques from the continuous domain, and, crucially, achieves high-quality categorical sample generation with very few inference steps.

Methodological Framework

CFMs are constructed upon a variational perspective of flow matching, notably leveraging the trajectory geometry on the probability simplex. The approach entails the following key components:

  • Endpoint Parametrization: Rather than parameterizing the instantaneous velocity field directly, CFMs predict the conditional expectation (partial denoiser) of the endpoint distribution at all intermediate times. This ensures that all interpolated states stay within the simplex, and the terminal distribution is discrete by construction.
  • Self-Distillation Losses: CFMs are trained with a cross-entropy endpoint matching loss, reflecting the categorical nature of the targets, and an associated Lagrangian Self-Distillation (CSD) loss. The CSD enforces self-consistency along learned flow-map trajectories.
  • Endpoint Consistency Lagrangian Distillation (ECLD): To stabilize and align magnitudes between losses, an endpoint-consistency loss based purely on cross-entropy is derived and shown to control the Lagrangian residual. This results in numerically stable and geometrically consistent learning signals. Figure 1

    Figure 1: Overview of CFM training; continuous interpolations on the probability simplex enable endpoint consistency and Lagrangian self-distillation.

Theoretically, these choices guarantee both the validity of the solution (since all predictions remain on the simplex) and the expressiveness needed for accurate sample transport from prior to target. Geometric confinement of paths ensures that large time-step flow-map jumps do not leave the valid data manifold, a critical failure mode for unconstrained flow matching approaches.

Test-Time Inference and Guidance

A notable property of CFMs is their plug-and-play compatibility with advanced test-time inference procedures. Because the flow map trajectory is entirely continuous on the simplex, standard score-based and classifier guidance, as well as sequential Monte Carlo sampling and reward reweighting techniques, transfer directly from the continuous setting.

For fine control, lookahead mechanisms via flow map endpoints allow accurate reward-tilting at test time. The use of soft (simplex-relaxed) states supports both straight-through and continuous reward functions, enabling effective discrete guidance via classifier or reward models.

Empirical Results

CFMs are evaluated across three discrete generation domains: molecular graphs (QM9, ZINC250K), binarized image synthesis (MNIST), and text (Text8, LM1B). Across all domains, the focus is on reducing inference cost (minimizing NFE) while maintaining or exceeding the sample quality of slower baselines.

Molecular Graph Generation

On QM9 and ZINC, CFMs demonstrate substantial advances over prior art in few-step categorical flow and discrete diffusion baselines, especially in the single and two-step (NFE=1/2) regime. Figure 2

Figure 2: Validity, uniqueness, and Fréchet ChemNet Distance (FCD) versus NFE; CFMs (both CSD, ECLD) improve significantly upon unconstrained flow maps (Naive) in both QM9 and ZINC.

Key numerical highlights:

  • On QM9, CFM-ECLD achieves 95.8% validity at NFE=1 (compared to 59.9% for Set2GraphVAE and 91.4% for MoFlow).
  • On ZINC, CFM-ECLD achieves 93.5% validity at NFE=1, far surpassing baselines.
  • At NFE=2, sample quality approaches that of full multi-step methods (that use up to 1000 steps) with a 50–500× reduction in computation. Figure 3

    Figure 3: Samples from the CFM-ECLD model on QM9, with a single function evaluation (NFE=1).

    Figure 4

    Figure 4: Samples from the CFM-ECLD model on ZINC, with a single function evaluation (NFE=1).

Image Generation and Guidance

On binarized MNIST, CFM models generate images with FID scores surpassing previous few-step baselines. Moreover, with reward-tilting at inference, CFM-generated images can be directed to desired classes (e.g., biasing towards digit zero) using classifier guidance. Figure 5

Figure 5

Figure 5: CFM samples on MNIST; left: unconditional, right: classifier reward-tilted toward zeroes.

Text Generation

CFMs attain strong negative log-likelihoods and perplexities, outperforming previously reported DFM and UDLM baselines, even operating in the low-NFE regime:

  • On Text8, NLL of 5.33 at NFE=1, consistently outperforming DFM ((2602.12233), Fig. 5).
  • On LM1B, Gen-PPL of 274.87 (as measured by GPT-2), beating UDLM in the low-NFE regime ((2602.12233), Fig. 6). Figure 6

    Figure 6: NFE vs. NLL on Text8, highlighting the efficiency-quality trade-off.

    Figure 7

    Figure 7: NFE vs. Gen-PPL on LM1B, measured by GPT-2.

Theoretical and Practical Implications

CFMs close a crucial gap between fast, self-distillable continuous flow models and the discrete (categorical) generative domain. The adoption of endpoint parametrization ensures geometric compatibility with categorical constraints, enabling both stable training and validity of generated samples, particularly in high-dimensional settings. The ECLD objective provides both theoretical guarantees, by provably controlling the Lagrangian residual, and empirical improvements in optimization and robustness.

Practically, CFMs allow scaling categorical generation tasks to larger and more demanding datasets while massively reducing inference costs. The plug-and-play compatibility with guidance and reward-tilting at test time further broadens their applicability, enabling controlled generation in scientific and natural language domains.

Directions for Future Work

Potential developments include:

  • Scaling CFMs to more complex structured data (e.g., protein sequences, large-scale text corpora), possibly with hierarchical or mixed discrete-continuous representations.
  • Integrating CFMs with advanced reward models and RL-style objectives for fine-grained conditional generation.
  • Exploring theoretical generalizations to flows on more abstract or constrained manifolds relevant for discrete combinatorial objects.

Conclusion

Categorical Flow Maps (2602.12233) introduce an effective, theoretically-sound, and computationally efficient framework for few-step generation in categorical settings. By leveraging endpoint-parametrized, simplex-constrained flow matching and robust self-distillation objectives, CFMs deliver high-quality samples in dramatically fewer inference steps than prior approaches, while unlocking advanced test-time guidance mechanisms for discrete data. The proposed framework stands as a principled bridge between consistency-driven continuous flows and accelerated categorical generative modeling.

File Document Download Save Streamline Icon: https://streamlinehq.com Markdown

Paper to Video (Beta)

Whiteboard

Explain it Like I'm 14

Explaining “Categorical Flow Maps” in Simple Terms

What is this paper about?

This paper is about teaching computers to create things made of symbols, like text, simple images made of black and white pixels, or molecular graphs, quickly and well. The authors introduce a new method called Categorical Flow Maps (CFM) that can generate these types of “categorical” data in just one or a few steps, instead of needing many slow steps like older methods.

What questions are the authors trying to answer?

The paper focuses on three main questions:

  • Can we make fast, high‑quality generators for symbolic data (letters, pixels, atoms), similar to recent “few‑step” image generators?
  • How do we design a model that stays within the rules of categorical data (probabilities that are non‑negative and add up to 1) while moving smoothly from “random noise” to a structured, valid output?
  • Can we let the model “teach itself” to make bigger, accurate jumps along the way, so we need fewer steps during generation?

How does the method work?

Think of generation as moving from a simple starting point (like a random mix of symbols) to a final, meaningful result (like a sentence or a molecule). The key ideas:

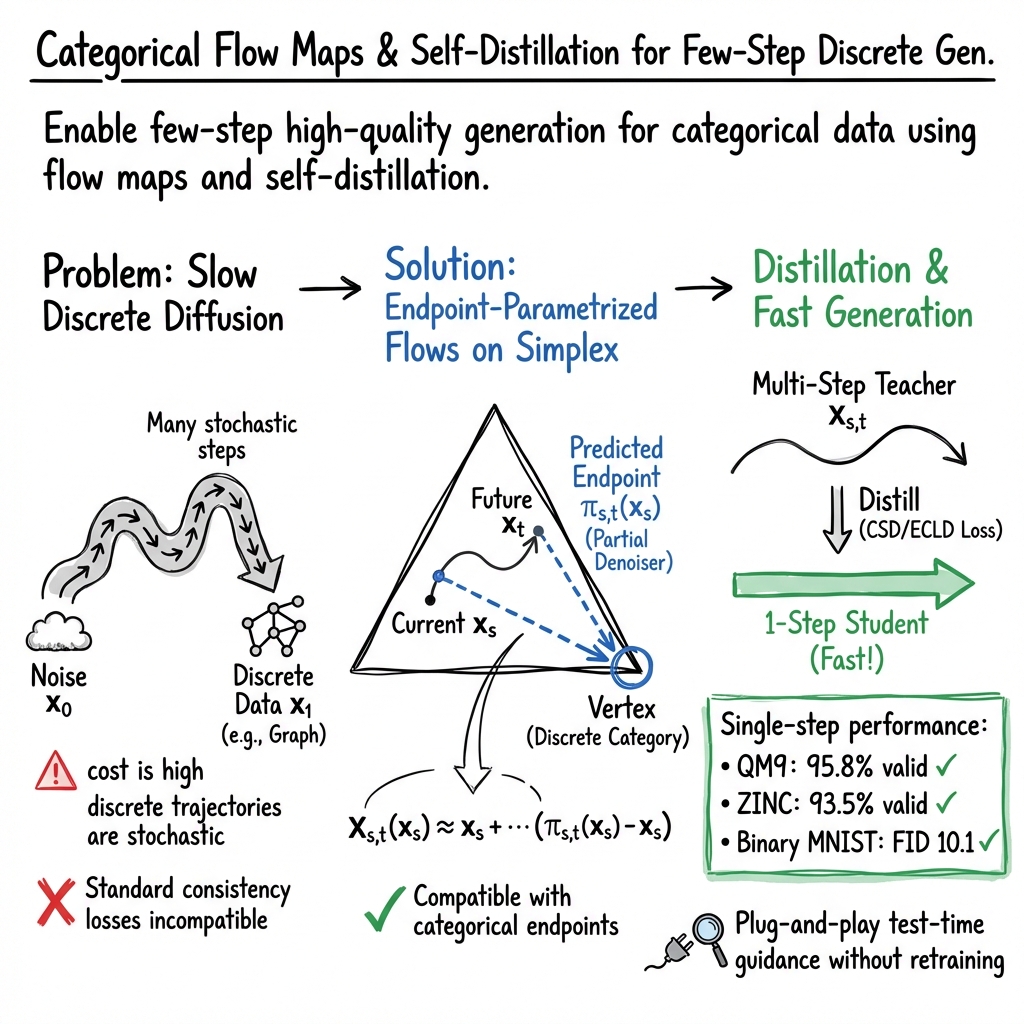
  • Probability pie chart: At every moment in time, the model keeps a “pie chart” of probabilities for each category (for example, which letter comes next, or whether a pixel is black or white). This pie chart lives on what mathematicians call the “simplex,” but you can think of it as a pie chart that always sums to 100%.
  • Flow map (a shortcut): Instead of taking many tiny steps, a flow map is like a smart shortcut or GPS route that lets the model jump from time s to time t in one go. It says, “Given where you are now, here’s where you’ll be a bit later.”
  • Endpoint prediction: Rather than predicting tiny movements directly, the model predicts where the probabilities should end up. That prediction keeps everything inside the valid pie chart. Training this is done with cross‑entropy, which is a standard way to measure “how wrong” a prediction is for categorical choices.
  • Self‑distillation (the model teaches itself): The model learns from its own better predictions. It uses a consistency rule: if you use the flow map to move forward, then your “endpoint prediction” at that new place should match what your “instant prediction” would say there. The paper introduces a stable, cross‑entropy version of this rule (called ECLD) that works well for categorical data.
  • Test‑time guidance (steering samples): During generation, you can steer the result toward goals you care about (for example, “make this image look like a ‘0’” or “make molecules that satisfy certain properties”). The model looks ahead with its flow map and adjusts the path to improve a reward, like a score from a classifier. A technique called Sequential Monte Carlo helps keep only the better‑scoring paths.

What did they find, and why is it important?

The authors show that Categorical Flow Maps can generate high‑quality results in very few steps across different kinds of categorical data:

  • Molecular graphs:
    • QM9: Up to 95.8% valid molecules in just 1 step, and 97.0% in 2 steps.
    • ZINC: 93.5% valid molecules in 1 step, improving with a few steps.
    • Their method competes with much slower baselines that need tens to thousands of steps.
  • Binary images (MNIST):
    • Better quality in few steps than a strong one‑step baseline (FID 10.1 at 1 step; lower is better).
    • Test‑time guidance successfully steers the model to draw target digits (e.g., zeroes) more reliably and with higher quality.
  • Text (Text8 and LM1B):
    • On Text8, they achieve lower negative log‑likelihood (NLL) than a strong baseline using fewer steps.
    • On LM1B, their method gives better generative perplexity (Gen‑PPL) in the low‑step regime compared to a strong baseline, showing faster, competitive performance.
    • Overall, their model can produce reasonable text with far fewer steps.

Why this matters:

  • Speed: Fewer steps means faster generation and lower compute cost.
  • Stability and correctness: By predicting endpoints on the probability pie chart, the model stays within valid categorical rules at all times.
  • Flexibility: It reuses powerful “consistency” training ideas from continuous models and brings them to discrete data like text and graphs.
  • Control: Test‑time guidance lets users steer generation toward desired goals without retraining the model.

What is the bigger impact?

This work helps close the gap between fast image generators and the slower methods typically used for text, graphs, and other symbol‑based data. With Categorical Flow Maps:

  • Developers can build quicker, controllable generators for discrete tasks, like molecule discovery, structured image synthesis, or text generation.
  • The approach is modular: it plugs into existing guidance tools and training tricks, making it practical to use.
  • It points toward a future where high‑quality generation of categorical data can be done in one or a few steps, saving time and resources while keeping outputs accurate and valid.

In short, the paper shows a simple, stable way to make fast, high‑quality generators for symbolic data by moving smoothly through probability space, teaching the model to take bigger accurate jumps, and allowing easy steering toward goals.

Ai Sparkles Streamline Icon: https://streamlinehq.com View Paper Prompt  List Streamline Icon: https://streamlinehq.com View All Prompts 

Knowledge Gaps

Knowledge gaps, limitations, and open questions

Below is a single, consolidated list of concrete gaps and open questions that remain unresolved and could guide future work.

  • Theoretical tightness and necessity of the ECLD bound: quantify when the inequality in Proposition 1 and Corollary 1 is tight, and characterize conditions under which minimizing CE-EC + TD provably recovers the true flow map.
  • Formal regularity assumptions for flow-map uniqueness: precisely state and verify the “mild regularity” conditions under which the learnt map is unique, and analyze whether these conditions hold for categorical, high-dimensional token spaces and graph-structured data.
  • Convergence guarantees of the endpoint-parametrized training objectives: establish global convergence rates and sample complexity for combined VFM + (CSD/ECLD) training, and characterize failure modes (e.g., bias induced by stop-gradient targets).
  • Stability near time one (t → 1): provide a principled justification for the weighting choice in CSD (empirically w_t ≡ 1 performed best), and derive robust weighting schedules that avoid instability while preserving theoretical guarantees.
  • Consistency across time intervals: verify transitivity and composition consistency (X_{s,u} ≈ X_{t,u} ∘ X_{s,t}) of learnt flow maps, and quantify errors when chaining few-step jumps vs. single long jumps.
  • Endpoint predictor temporal drift control: study how the TD regularizer interacts with model capacity and time discretization; develop stronger or adaptive regularizers that reduce ∂t π{s,t} without over-smoothing or harming fidelity.
  • Variational family expressiveness: go beyond mean-field categorical factorization to structured variational families (e.g., autoregressive or graphical posteriors) that can model inter-token/edge dependencies, and quantify gains in accuracy vs. cost.
  • Discretization at time one: clarify whether X_{0,1}(x_0) lands exactly on simplex vertices (one-hot) or requires rounding/sampling; analyze the impact of discretization schemes on distributional fidelity and calibration.
  • Flow map vs. velocity-field mismatch: explain why ECLD exhibits a gap between flow-map sampling and Euler integration at larger NFEs; derive training modifications that align the learned flow map with the underlying instantaneous velocity field over longer horizons.
  • Prior choice and interpolant design: systematically study how the continuous prior p_0 and the straight-line interpolant (α_t = 1 − t, β_t = t) affect performance; evaluate geometry-aware alternatives (e.g., Fisher–Rao geodesics, spherical parametrizations) for categorical paths.
  • Guidance correctness and variance: provide a formal analysis of reward tilting with SMC in the categorical setting (bias, variance, consistency), including the effect of lookahead via X_{t,1} vs. π_{t,t}, and quantify how STE vs. soft-input guidance affects gradients and sample quality.
  • Scaling to very large vocabularies: assess computational/memory bottlenecks of simplex-constrained endpoints for K ≈ 30k (LM1B), explore efficient approximations (sampled/hierarchical softmax, factorized logits), and measure scaling laws with sequence length and K.
  • Entropy and mode coverage in text: diagnose the observed entropy drop on LM1B, develop quantitative mode coverage metrics for discrete generative models, and identify architectural/training remedies (e.g., longer training, improved embeddings, temperature or entropy regularization).
  • Benchmark comparability: run controlled comparisons against Duo (and other few-step discrete baselines) on the same datasets and pipelines (Text8, LM1B), to isolate method effects from evaluation discrepancies; include OpenWebText where prior baselines report results.
  • Evaluation metrics for text: complement Gen-PPL from external LMs with ground-truth NLL (if tractable), human judgments, and diversity metrics; analyze sensitivity of Gen-PPL to the choice of evaluator model and dataset mismatch.
  • Graph validity guarantees: move beyond empirical validity to incorporate formal constraints (e.g., valency, charge conservation) into training or inference, and quantify how guidance or structured posteriors affect the rate of invalid molecules.
  • Robustness and OOD generalization: test CFMs under distribution shifts (e.g., domain transfer for text, larger molecule classes), measure robustness of few-step sampling, and study failure modes under noisy or adversarial rewards.
  • Training efficiency vs. autoregressive baselines: report training cost, memory footprint, and wall-clock comparisons; determine whether few-step inference gains offset training overheads in realistic deployment scenarios.
  • Hyperparameter and architecture sensitivity: provide comprehensive ablations (embedding layers, JVP kernels, compilation settings, time-sampling strategies, loss weights) to identify which components are critical for stability and performance across modalities.
  • Applicability beyond binary images: evaluate CFMs on multi-class per-pixel categorical image tasks (e.g., color quantization, segmentation) to test scalability and guidance efficacy in higher-dimensional categorical outputs.
  • Teacher-free consistency training: investigate whether purely student-based self-consistency (without stop-gradient teacher targets) is viable in the categorical setting, and under what conditions it remains stable.
  • Structured constraints in guidance: extend reward tilting to include domain-specific constraints for molecules or syntax constraints for text, and quantify trade-offs between constraint satisfaction and sample quality.
  • Error accumulation in multi-step jumps: derive theoretical and empirical bounds on error compounding when chaining few-step flow maps, and propose correction schemes (e.g., local re-distillation or adjoint consistency losses).
  • Reproducibility and standardization: release standardized pipelines for categorical few-step benchmarking (datasets, metrics, evaluator models, SMC settings), enabling consistent cross-method comparisons.
Ai Sparkles Streamline Icon: https://streamlinehq.com View Paper Prompt  List Streamline Icon: https://streamlinehq.com View All Prompts 

Practical Applications

Immediate Applications

The following use cases can be deployed with today’s tooling, leveraging the paper’s Categorical Flow Maps (CFMs), simplex-constrained endpoint parameterization, and test-time reward steering with SMC.

  • Fast molecular graph generation and pre-screening
    • Sectors: healthcare, pharma/biotech, materials
    • What: Generate large batches of chemically valid molecules in 1–2 steps; steer toward target properties using classifier rewards and SMC (e.g., QED, logP, toxicity).
    • Tools/products/workflows:
    • CFM-based molecule generators integrated with RDKit for valency checks and property evaluation.
    • “CFM-guided sampler” modules that plug into existing QSAR pipelines for rapid candidate triaging.
    • Assumptions/dependencies:
    • Availability/quality of differentiable property predictors or classifiers.
    • Graph representation fidelity (atom/bond vocabularies) and training data coverage.
    • SMC parameters tuned to avoid degeneracy while meeting latency constraints.
  • Low-latency, few-step generation for tokenized media pipelines
    • Sectors: media/creative tools, mobile software
    • What: Replace multi-step sampling over discrete codebooks (e.g., VQ-VAE tokens for images/audio) with 1–4 step CFMs to reduce latency and energy costs.
    • Tools/products/workflows:
    • Drop-in CFM samplers for token-based image/music generation.
    • On-device or web-scale deployment with reduced NFEs.
    • Assumptions/dependencies:
    • High-quality tokenizers/codebooks.
    • Training stability on large vocabularies; proper tuning of ECLD/CSD losses.
  • Inference-time control/guardrails for discrete generation
    • Sectors: software, consumer apps, platform safety (policy relevance)
    • What: Use reward-tilting with flow-map lookahead to steer text or token sequences toward safety, style, or task objectives (toxicity reduction, factuality, brand voice) without retraining.
    • Tools/products/workflows:
    • Plug-and-play SMC-guided sampling layers; straight-through estimator (STE) integration for reward gradients on discrete outputs.
    • Policy-aligned reward models (toxicity/fairness/factuality) applied during generation.
    • Assumptions/dependencies:
    • Reward models must be robust and calibrated; Goodhart’s law risks.
    • Latency/compute overhead of SMC and reward evaluation.
  • On-device, domain-specific autocomplete and assistive writing
    • Sectors: mobile, productivity software, education
    • What: Small CFMs for low-latency text prediction on limited vocabularies (e.g., custom keyboards, templated text) with test-time style/constraint steering.
    • Tools/products/workflows:
    • CFMs trained on domain-specific corpora; reward-guided style/grammar constraints at inference.
    • Assumptions/dependencies:
    • Model capacity vs. vocabulary size; careful embedding design for stability.
    • Quality of domain data; privacy-preserving training when needed.
  • Rapid academic iteration for discrete generative modeling
    • Sectors: academia, R&D labs
    • What: Few-step CFMs reduce sampling compute for ablations, hyperparameter sweeps, and benchmarking on discrete modalities (text, graphs).
    • Tools/products/workflows:
    • Reusable CFM training/evaluation code with ECLD/CSD; standard cross-entropy endpoint training.
    • Assumptions/dependencies:
    • Reproducibility when scaling to larger vocabularies/longer sequences.
  • Targeted data augmentation in discrete domains
    • Sectors: ML engineering, cybersecurity, software QA
    • What: Generate constraint-satisfying sequences (e.g., rare code patterns, test-case strings) by tilting toward classifier-defined properties at inference.
    • Tools/products/workflows:
    • “Reward-tilted augmentation” pipelines with SMC resampling to focus on edge cases.
    • Assumptions/dependencies:
    • Reward model coverage of target edge cases; careful monitoring to avoid distributional drift.
  • Compute/energy footprint reduction for generative workloads
    • Sectors: IT operations, sustainability (policy relevance)
    • What: Cut sampling NFEs compared to discrete diffusion or autoregressive baselines; useful for green-AI initiatives.
    • Tools/products/workflows:
    • Ops dashboards measuring NFE reductions and energy savings.
    • Assumptions/dependencies:
    • Comparable task quality at low NFE must be validated per deployment; model compression/quantization may be complementary.

Long-Term Applications

These opportunities require further research, scaling, or integration beyond the current empirical scope (e.g., larger vocabularies, longer contexts, richer constraints, formal guarantees).

  • General-purpose, non-autoregressive LLMs
    • Sectors: software, consumer AI, enterprise AI
    • What: Scale CFMs to replace or complement autoregressive LMs for fast, controllable generation at similar quality.
    • Potential tools/products/workflows:
    • CFM-based chat assistants with inference-time guardrails (toxicity/factuality) and multi-objective rewards.
    • Assumptions/dependencies:
    • Training stability on very large vocabularies and contexts; entropy calibration; extensive compute and data.
  • End-to-end drug design with multi-objective, synthesis-aware constraints
    • Sectors: pharma/biotech
    • What: Integrate CFMs with ADMET predictors, retrosynthesis planners, and multi-constraint reward tilting for property-balanced molecules.
    • Potential tools/products/workflows:
    • “Design→Retrosynthesis→Feasibility check” workflows with SMC to enforce hard constraints.
    • Assumptions/dependencies:
    • High-quality predictors; robust multi-objective balancing; integration with wet-lab loops and regulatory validation.
  • Certified safe-by-construction generative systems
    • Sectors: policy/regulation, platforms, finance/healthcare compliance
    • What: Formalize and verify inference-time constraints (safety, fairness, privacy) enforced via reward tilting and flow-map lookahead; provide auditable guardrails.
    • Potential tools/products/workflows:
    • Compliance dashboards; certifiable reward models; logging of SMC resampling decisions.
    • Assumptions/dependencies:
    • Verified reward models and calibration; standards for auditability; formal guarantees on constraint satisfaction.
  • Real-time sequence generation for robotics and planning
    • Sectors: robotics, logistics, operations research
    • What: Generate discrete action sequences in few steps with constraints (safety zones, resource limits) using reward-tilted CFMs.
    • Potential tools/products/workflows:
    • Planners that compose CFMs with symbolic constraints or hierarchical controllers.
    • Assumptions/dependencies:
    • Reliable downstream evaluators/reward functions; tight latency budgets; integration with continuous control.
  • High-fidelity financial sequence simulation and stress testing
    • Sectors: finance, risk management
    • What: Generate market/order-book event sequences quickly; tilt toward rare/stress scenarios for risk analysis without retraining.
    • Potential tools/products/workflows:
    • Scenario generators with SMC to explore tail risks; compliance-aware filters.
    • Assumptions/dependencies:
    • Robustness to distribution shift; governance of reward design to avoid perverse incentives.
  • Multimodal generative codecs with discrete tokens (images/audio/video)
    • Sectors: media, communications, edge computing
    • What: Use CFMs over discrete codebooks to enable fast decoding, streaming, and on-device creative tools.
    • Potential tools/products/workflows:
    • Real-time editors and creative apps with low-latency generative feedback.
    • Assumptions/dependencies:
    • High-quality tokenizers; latency/quality trade-offs; hardware acceleration.
  • Privacy-preserving EHR/code sequence synthesis for analytics
    • Sectors: healthcare IT, cybersecurity
    • What: Generate discrete records/code sequences with reward tilting toward privacy (e.g., k-anonymity proxies) and utility (target statistics).
    • Potential tools/products/workflows:
    • Synthetic data generators with differential privacy-aware reward models.
    • Assumptions/dependencies:
    • Validated privacy metrics; legal/regulatory alignment; robust utility–privacy balancing.
  • Personalized education content generation with constrained difficulty and curriculum
    • Sectors: education technology
    • What: Generate exercises/questions with controlled difficulty and topical coverage via inference-time reward steering.
    • Potential tools/products/workflows:
    • Curriculum-aware generators integrated into LMS platforms.
    • Assumptions/dependencies:
    • Accurate difficulty estimators; safety/age-appropriateness classifiers; dataset curation.
  • Edge-device generative AI with strict power/latency budgets
    • Sectors: mobile, wearables, automotive
    • What: Deploy CFMs for tokenized tasks (speech units, command sequences) with very few steps, reducing energy consumption.
    • Potential tools/products/workflows:
    • Hardware-friendly CFM runtimes; compilers using JVP/efficient kernels as described in the paper.
    • Assumptions/dependencies:
    • Further optimization of kernels and memory; model compression; robustness tests on-device.

Notes on feasibility across applications:

  • CFMs depend on stable training with ECLD/CSD and appropriate weighting; large vocabularies/long contexts may require architectural refinements (embeddings, kernels, compiler optimizations).
  • Reward-tilted sampling quality hinges on the accuracy and calibration of reward models; SMC adds control but also complexity and overhead.
  • For safety/ethics use cases, classifier brittleness and distribution shifts remain key risks; monitoring and auditing are essential.
  • Success in small benchmarks (e.g., QM9, Text8, binarized MNIST) is promising, but translating to large-scale, production-grade settings will require additional research, scaling, and rigorous validation.
Ai Sparkles Streamline Icon: https://streamlinehq.com View Paper Prompt  List Streamline Icon: https://streamlinehq.com View All Prompts 

Glossary

  • Autoregressive: A generative modeling approach that produces each token conditioned on previous tokens. "competitive performance relative to strong autoregressive baselines~\citep{llada}"
  • Categorical Flow Maps (CFM): A flow-matching method that transports a continuous prior to a discrete target distribution for few-step categorical generation. "We introduce Categorical Flow Maps (CFM), a simple flow matching construction for discrete data that learns a flow map transporting a continuous prior to a discrete target distribution."
  • cross-entropy: A loss function for categorical distributions measuring the divergence between predicted probabilities and the true category. "a categorical distribution Cat(x1∣πtθ(x))\mathrm{Cat}(x_1\mid \pi_{t}^\theta(x)) over KK classes yields a cross-entropy objective, which keeps endpoint predictions on the simplex ΔK:={p∈RK: pk≥0, ∑k=1Kpk=1}\Delta^K := \{p\in\mathbb{R}^{K}:\ p_k\ge 0,\ \sum_{k=1}^{K} p_k=1\} by construction."
  • Dirichlet distributions: Probability distributions over the simplex commonly used to model categorical probabilities. "~\citet{stark2024dfm} claim that linear paths supported on the simplex are limited and thus construct paths based on the Dirichlet distributions, but therefore introduces terms unstable in higher dimensions and fails to scale."
  • drift: The deterministic component of the probability flow (vector field) governing the evolution of states over time. "where the drift, bb, is given by the conditional expectation"
  • Euler integration: A simple numerical method for integrating differential equations by stepping along the vector field. "Euler integration of the learned instantaneous velocity field."
  • Eulerian: A formulation that models velocities at fixed spatial locations rather than following individual trajectories (contrast with Lagrangian). "which can be understood as Eulerian and Lagrangian formulations, respectively."
  • Endpoint-Consistent Lagrangian Distillation (ECLD): A self-distillation objective using cross-entropy and endpoint predictions that provably bounds the Lagrangian residual. "We show that such an objective is achievable through the following Endpoint-Consistent Lagrangian Distillation (ECLD) loss bound"
  • endpoint parametrisation: Modeling flow maps via predicted endpoints on the simplex instead of direct velocity vectors. "Instead of the vector-based vs,tv_{s,t} parametrisation, we opt for an endpoint one:"
  • Fisher-Rao metric: A Riemannian metric on the probability simplex that induces geometrically principled paths. "~\citet{fisherflow,categoricalflowmatching} endow the simplex with the Fisher-Rao metric and leverage the isometry to the scaled positive orthant of the sphere"
  • flow map: A map that transports a state from time s to time t along the learned probability flow. "We define the flow map, $X:[0,1]^2\timesR^d\toR^d$, for any two times (s,t)∈[0,1]2(s,t)\in[0,1]^2, as the map which brings xsx_s to xtx_t"
  • flow matching: A training framework that learns the velocity field or flow that transports a prior distribution to the data distribution. "These losses are jointly optimised with a standard flow matching loss on vt,tθv_{t,t}^\theta."
  • Fréchet ChemNet Distance (FCD): A metric for evaluating molecular generative models based on learned feature statistics. "while achieving an FCD competitive with strong multi-step flow-based baselines."
  • Fréchet Inception Distance (FID): A metric for assessing image generation quality by comparing feature distributions. "10.1 FID on Binary MNIST"
  • Generative Perplexity (Gen-PPL): A measure of text generation quality using a pretrained LLM’s perplexity over generated samples. "LM1B with $274.87$ Gen-PPL."
  • KL divergence: A measure of divergence between probability distributions, often used for variational training objectives. "minimizes a time-averaged KL divergence to approximate the posterior pt(x1∣xt)p_t(x_1 \mid x_t) of the probability path"
  • Lagrangian condition: The identity relating the time derivative of the flow map to the instantaneous velocity (via endpoint predictions). "The second one is the Lagrangian condition, which enables self-distillation training."
  • Lagrangian residual: The residual error in satisfying the Lagrangian condition during flow-map self-distillation. "[ECLD controls the Lagrangian residual]"
  • Lagrangian self-distillation (LSD): A training objective that distills flow maps by matching their time derivatives to instantaneous velocities. "we focus on the Lagrangian self-distillation (LSD) objective, which offers the best empirical performance:"
  • Markov chain: A stochastic process with memoryless transitions used to model discrete diffusion processes. "the forward and reverse processes are modelled as Markov chains, in either discrete~\citep{d3pm,mdlm,sedd,shi2025md4} or continuous time~\citep{campbell2022continuous, sun2023scorebased, campbell2024dfm}."
  • Mean Flows: A few-step generative modeling method that learns mean trajectories for accelerated sampling. "Strong empirical results for few-step generation on images have been demonstrated using Mean Flows~\citep{geng2025meanflows,geng2025improvedmeanflowschallenges}"
  • number of function evaluations (NFE): The count of network calls during sampling, serving as a measure of inference cost. "as a function of the number of function evaluations (NFE) on the QM9 dataset."
  • partial denoiser: An endpoint predictor used to define flow maps that transport noisy states toward cleaner endpoints. "We refer to πs,t\pi_{s,t} as a partial denoiser."
  • probability flow: The dynamical system describing how the probability path evolves over time via a learned vector field. "moreover, by its differentiability, the path also defines a probability flow, given by"
  • probability path: A time-indexed sequence of distributions connecting the prior and data distributions. "Thus, ItI_t induces a probability path, (pt)t∈[0,1](p_t)_{t\in[0,1]}"
  • probability simplex: The set of non-negative vectors that sum to one, representing categorical distributions. "paths on a probability simplex"
  • reward-tilted distribution: A distribution modified by exponentiated reward to guide sampling toward desired properties. "sample from a reward-tilted distribution p~(x):=p(x)er(x)+F,\tilde{p}(x) := p(x) e^{r(x) + F},"
  • score: The gradient of the log-density used for stochastic sampling and guidance. "where st(xt)=(tvt,t(xt)−xt)(1−t)−1s_t(x_t) = (t v_{t,t} (x_t) - x_t) (1-t)^{-1} denotes the score"
  • Sequential Monte-Carlo (SMC): A sampling technique using importance weights and resampling to track a target distribution. "we use sequential Monte-Carlo (SMC) sampling during generation"
  • self-distillation: Training a model to match its own (or a teacher’s) predictions to enable accelerated inference. "a general framework for self-distillation through flow maps"
  • straight-through (STE) discretization: A technique that allows discrete forward passes while propagating gradients through continuous relaxations. "apply a straight-through (STE) discretization to Xt,1(xt)X_{t,1}(x_t)"
  • stochastic interpolant: A stochastic process that continuously interpolates between a prior sample and a data sample. "A stochastic interpolant is a stochastic process, $I:[0,1]\timesR^d\timesR^d\toR^d$, that continuously interpolates between x0∼p0x_0 \sim p_0 and x1∼p1x_1 \sim p_1"
  • Terminal Velocity Matching: A few-step training method that focuses on matching terminal velocities of flows. "Terminal Velocity Matching~\citep{zhou2025terminalvelocitymatching}, which can be understood as Eulerian and Lagrangian formulations, respectively."
  • variational family: A parametric family of distributions used to approximate a posterior in variational training. "the mean of a variational family qtθ(x1∣xt)q_t^\theta(x_1 \mid x_t)."
  • Variational Flow Matching (VFM): A formulation that learns endpoint-conditioned distributions to recover the flow’s velocity field. "Variational Flow Matching (VFM) formulates the learning problem in terms of an estimate for μt\mu_t rather than btb_t."
  • velocity field: The vector field describing instantaneous movement in the probability flow at each time. "still retrieves the instantaneous vector field of the probability flow."
  • Wiener process: A mathematical model of Brownian motion used in stochastic differential equations. "and (Wt)t∈[0,1](W_t)_{t\in[0,1]} is a standard Wiener process."
Ai Sparkles Streamline Icon: https://streamlinehq.com View Paper Prompt  List Streamline Icon: https://streamlinehq.com View All Prompts 

Open Problems

We found no open problems mentioned in this paper.

Collections

Sign up for free to add this paper to one or more collections.

User Circle Single Streamline Icon: https://streamlinehq.com Sign Up

Tweets

Sign up for free to view the 12 tweets with 554 likes about this paper.

User Circle Single Streamline Icon: https://streamlinehq.com Sign Up for Free