Neural Local Wasserstein Regression (2511.10824v1)

Abstract: We study the estimation problem of distribution-on-distribution regression, where both predictors and responses are probability measures. Existing approaches typically rely on a global optimal transport map or tangent-space linearization, which can be restrictive in approximation capacity and distort geometry in multivariate underlying domains. In this paper, we propose the \emph{Neural Local Wasserstein Regression}, a flexible nonparametric framework that models regression through locally defined transport maps in Wasserstein space. Our method builds on the analogy with classical kernel regression: kernel weights based on the 2-Wasserstein distance localize estimators around reference measures, while neural networks parameterize transport operators that adapt flexibly to complex data geometries. This localized perspective broadens the class of admissible transformations and avoids the limitations of global map assumptions and linearization structures. We develop a practical training procedure using DeepSets-style architectures and Sinkhorn-approximated losses, combined with a greedy reference selection strategy for scalability. Through synthetic experiments on Gaussian and mixture models, as well as distributional prediction tasks on MNIST, we demonstrate that our approach effectively captures nonlinear and high-dimensional distributional relationships that elude existing methods.

• The paper introduces a novel local regression model in Wasserstein space that uses neural networks to parametrize measure-dependent transport maps.
• It employs adaptive kernel weighting and specialized architectures like DeepSets and U-Net to capture localized, nonlinear distributional transformations.
• Empirical evaluations on Gaussian mixtures and MNIST show high accuracy with low test errors, demonstrating practical scalability and robustness.

Neural Local Wasserstein Regression: A Technical Assessment

Problem Formulation and Motivations

The paper "Neural Local Wasserstein Regression" (2511.10824) addresses the regression problem where both predictors and responses are probability measures, a substantial setting in modern statistics, computer vision, and scientific computing. Classical and most recent frameworks approach distribution-on-distribution (DoD) regression using global optimal transport (OT) maps or tangent-space linearizations, but these methods have inherent limitations: global optimality or linear structures are insufficiently expressive when modeling complex relationships between high-dimensional or non-Euclidean distributions. This work introduces a localized approach to DoD regression, combining kernel methods in Wasserstein space with neural architectures to parameterize flexible local transport maps.

Methodological Framework

Local Regression Model in Wasserstein Space

The formulation is a nonparametric regression of probability measures, formalized as:

$\nu = T_{\varepsilon}\#(T_{\mu}\#\mu)$

where $\mu$ and $\nu$ are source and target measures, $T_{\mu}$ is a measure-dependent regression map, and $T_{\varepsilon}$ encodes mean-preserving noise. This structure contrasts with traditional works that enforce a global operator, $T_0$, which is empirically less robust and theoretically insufficient for nontrivial or high-dimensional DoD tasks.

The crucial departure is that $T_{\mu}$ depends explicitly on the local geometry of $\mu$, allowing for a rich class of transformations not accessible to global maps or tangent linearizations.

Kernel Weighting and Locality

To effect local regression in Wasserstein space, the method leverages a kernel weighting scheme:

$K_h(\mu, \mu_i) = h^{-d}K(W_2(\mu, \mu_i) / h)$

where $K$ is a smooth symmetric kernel and $h$ is the bandwidth, adaptively tuned per reference measure using a $k$-nearest neighbor heuristic to maintain statistical efficiency despite sparsity or heterogeneity of the distributional dataset.

Objective Function

The local regression operator is estimated by minimizing a kernel-weighted empirical loss:

$$\hat{T}_\mu = \arg\min_T \frac{1}{n} \sum_{i=1}^n W_2^2(T\#\mu_i, \nu_i) K_h(\mu, \mu_i)$$

where the Wasserstein-2 distance is approximated with Sinkhorn regularization for computational efficiency and differentiability.

Neural Architectures for Local Regression

DeepSets for Empirical Distributions

The permutation invariance of sampled points from empirical distributions is handled by DeepSets-style architectures. For each local regression operator centered at reference $\mu_0^{(l)}$, a neural network maps point clouds to affine or nonlinear transport maps via:

$$f_l(X_i) = \rho_l\left( \frac{1}{k}\sum_{j=1}^k \psi_l(x_j^{(i)}) \right)$$

where $\psi_l$ is a shared MLP encoder and $\rho_l$ outputs parameters for the map (e.g., affine coefficients or displacement fields). This model class is suitable for both synthetic Gaussian and Gaussian mixture settings.

U-Net for Images

For distributions with grid support, specifically images (e.g., MNIST digit transformations), a compact U-Net is employed for image-to-image DoD regression. This architecture efficiently encodes spatial and semantic relationships and outputs a probability map interpreted as a predicted measure after softplus activation and normalization.

Empirical Evaluation

Experiments on several settings validate the efficacy of the approach:

Gaussian and Gaussian Mixture Tasks

Local affine neural transport maps perform robustly on synthetic experiments, accurately capturing nonlinear ground-truth relationships when sufficient local data is available. Most notably, in 2D Gaussian mixture settings with $n=1000$, $k=1000$, the absolute test error can be as low as $0.00124 \pm 0.00011$ with $R_W^2 = 0.99983$, demonstrating high-fidelity reconstruction of distributional transformations. Performance drops in higher dimensions if kernel bandwidth and data sparsity are not well controlled, reflecting the inherent curse of dimensionality.

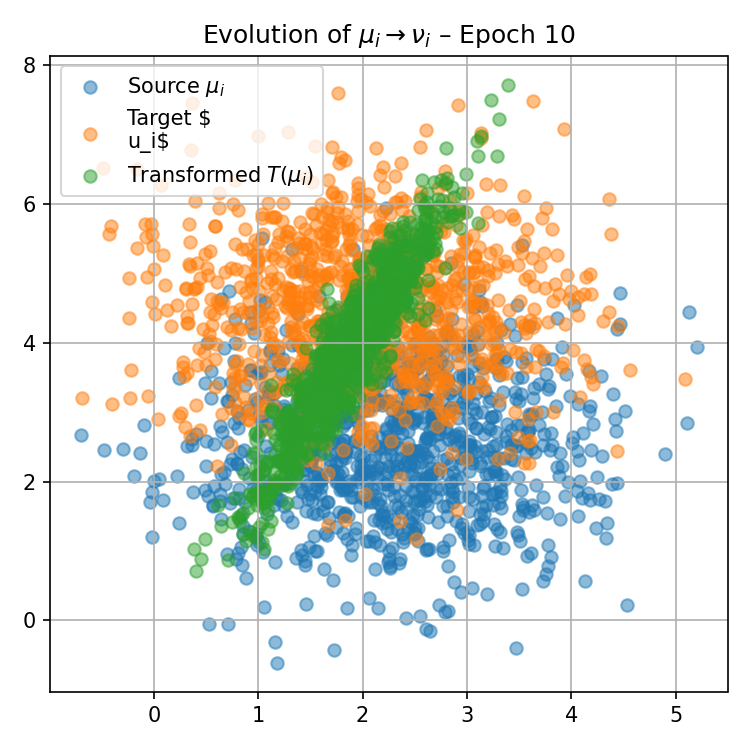
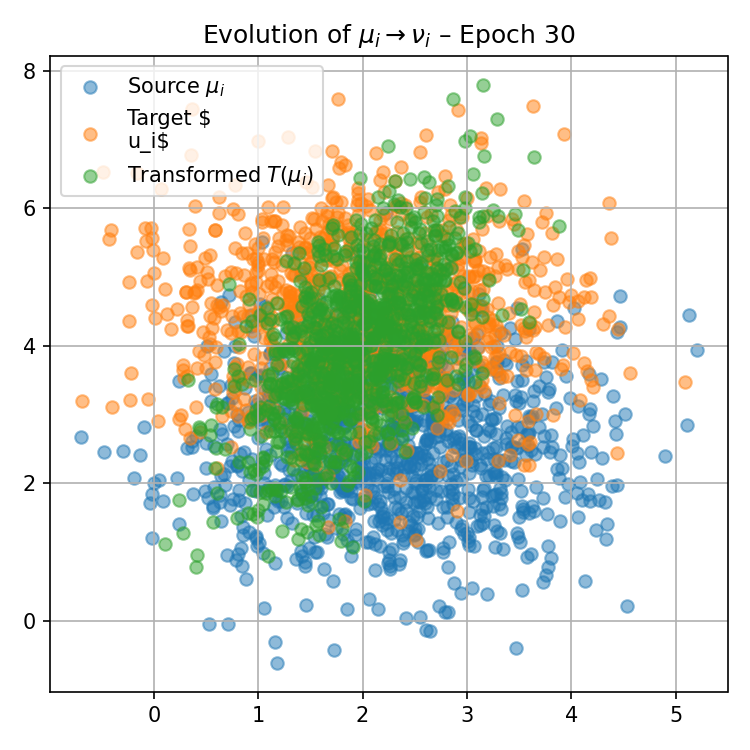
Figure 1: Visualization of the progression of pushforward distributions for a fixed reference measure $\mu_0^{(0)}$ during training, illustrating how local maps adapt to match target distributions over epochs.

MNIST Distributional Regression

The method is further evaluated on MNIST, treating input and output digits as discrete probability distributions on $[0,1]^2$. U-Net-based local regressors successfully predict target digit distributions from source digits, with visually plausible and quantitatively accurate outputs, even under intra-class variability.

Technical and Practical Implications

This work presents several important advancements:

• Expanded Approximation Power: By eschewing global map constraints, local regression models represent a broader class of distributional relations—including nonlinear, non-monotone, or piecewise smooth transport maps. This substantially increases modeling flexibility in practice.
• Scalable Training and Inference: Through the greedy selection of reference measures and modular deployment of local models, scalability to large datasets or complex measure spaces is achieved without incurring the instability or overfitting of global approaches.
• Permutation and Spatial Symmetry Preservation: DeepSets and U-Net architectures, chosen per data modality, guarantee invariance properties critical to measure-based learning.
• Explicit Handling of Distribution Shift: The model's structure, allowing the local transport map $T_\mu$ to be indexed by unseen test measures, addresses distribution shift in inference—a significant advantage over operator learning methods that regress to the training support.

Limitations and Theoretical Outlook

While the empirical performance is strong, several areas require further theoretical development:

• The identifiability and statistical consistency of local regression operators $T_\mu$ remain open.
• Kernel bandwidth $h$ selection, despite adaptivity via $k$NN, is sensitive, especially in higher dimensions; theoretical analysis of optimal scaling and rates is desirable.
• The curse of dimensionality persists for large $d$, as local neighborhoods become sparse in Wasserstein space, potentially degrading both statistical and computational efficiency.

Future Directions

This methodological innovation opens promising avenues:

• Formal study of minimax rates and regularity conditions for kernelized local regression maps in Wasserstein space.
• Extension to conditional or hierarchical DoD regression with functional or manifold-valued measures.
• Application to complex domains (medical imaging, spatiotemporal field prediction, generative modeling) where geometric invariances, local adaptation, and measure-valued data are crucial.

Conclusion

Neural Local Wasserstein Regression presents a substantive step forward in nonparametric distribution-on-distribution regression, combining kernel smoothing under Wasserstein geometry with neural parameterizations to learn flexible, locally adaptive transport maps. The framework effectively overcomes limitations of global map and tangent-space methods, offering improved expressivity and empirical robustness for high-dimensional or heterogeneous distributional datasets. The approach carries both practical utility and theoretical interest, with open questions on optimality, regularization, and broader generalization capabilities.