- The paper introduces a control-theoretic framework to learn optimal paths for dynamic measure transport, mitigating artifacts in common geometric annealing paths.
- It employs Gaussian process PDE methods in RKHS to regularize both the drift field and tilting function, ensuring smoother and more efficient sampling.
- The learned interpolation significantly outperforms reference paths in multimodal scenarios by better aligning mass distribution and reducing error metrics.
Learning Paths for Dynamic Measure Transport: A Control Perspective
Introduction and Motivation
This paper addresses the problem of identifying optimal paths of probability measures for sampling via dynamic measure transport (DMT), with a particular focus on the control-theoretic perspective. DMT-based sampling methods, including neural ODEs, continuous normalizing flows, and diffusion models, rely on constructing a stochastic process that transforms samples from a reference distribution η into samples from a target distribution π. The evolution of the process is governed by a drift (velocity) field v and, optionally, a diffusion term. The choice of the path of intermediate measures (ρ(t))t∈[0,T] is critical for the tractability and efficiency of the sampling procedure.
The paper highlights that commonly used paths, such as the geometric annealing path μ(t)∝η1−tπt, may be suboptimal for certain (η,π) pairs, leading to irregular or inefficient transport dynamics. The authors propose a flexible family of optimization problems for learning "tilted" paths of measures, advocating for explicit regularization terms that promote smoothness in the velocity field. The connection to mean-field games (MFGs) is established, providing a principled framework for path selection and regularization.
Issues with Canonical Paths and the Need for Learned Interpolations
The geometric annealing path is widely used due to its tractable log-derivative and connections to Fisher–Rao geometry. However, for multimodal targets or poorly aligned reference and target distributions, this path can induce undesirable transport phenomena, such as "teleportation of mass" between modes, which are difficult to capture with standard DMT algorithms. The paper demonstrates this with a mixture-of-Gaussians example, where the geometric path fails to allocate sufficient mass to the left mode of the target.
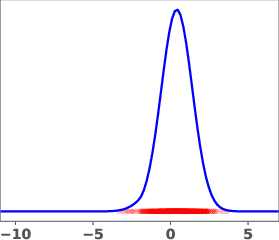
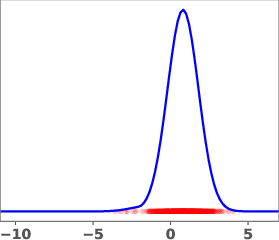
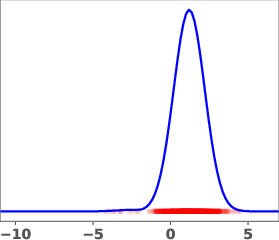
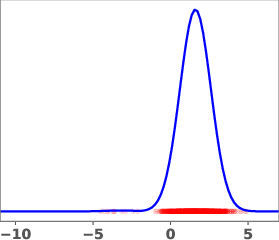
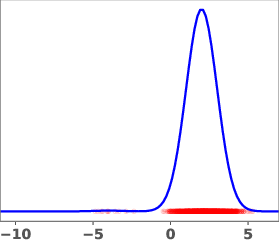
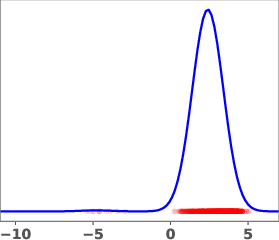
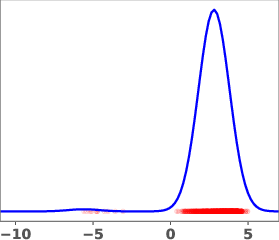
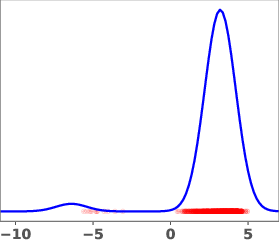
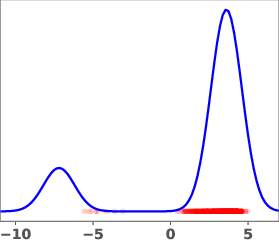
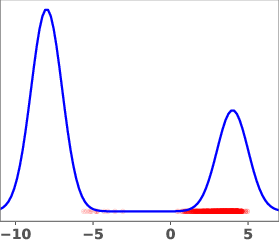
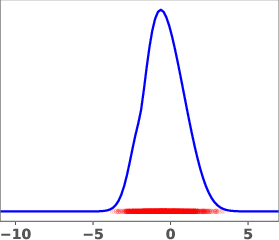
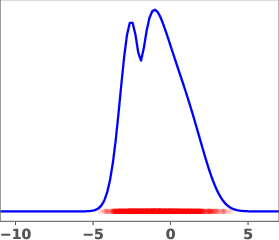
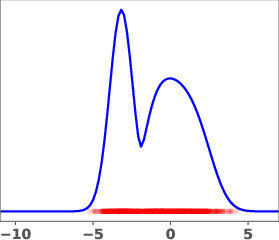
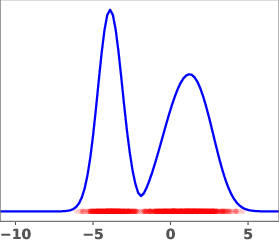
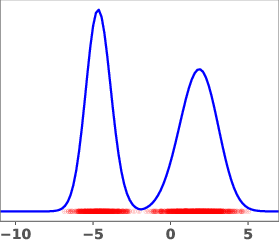
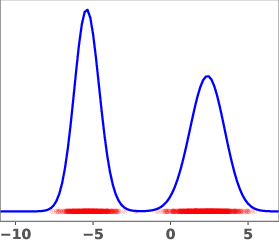
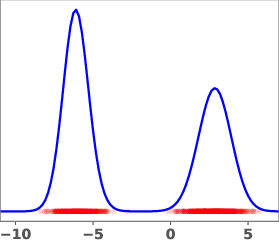
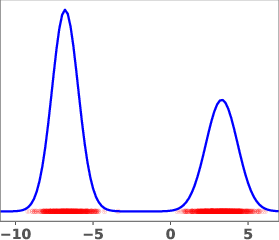
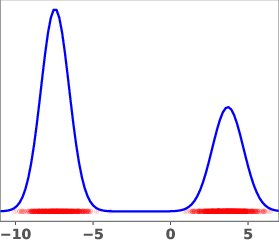
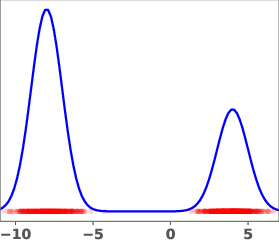
Figure 1: Geometric annealing path (top) and path resulting from solving the proposed control problem for a mixture-of-Gaussians example. Samples generated by the respective velocity fields are overlaid in red.
The authors propose to learn a tilting function g(x,t) that perturbs the reference path, yielding a new path ρg(x,t)∝μ(x,t)eg(x,t). This approach is motivated by prior work using PINN-based optimization, but the paper provides a more principled control-theoretic formulation, connecting the problem to MFGs and explicit regularization.
The central contribution is the formulation of a control problem for path identification:
v∈V,g∈Ginf∥v∥V2+λg∥g∥G2s.t.−∇⋅(vρg)=ρg(∂tlogρg),ρg∝ρrefeg,g(⋅,0)=g(⋅,1)≡0
This framework allows for the use of general Banach or RKHS norms to regularize both the velocity and the tilting function, promoting smoothness and tractability. The constraints enforce exact matching of the terminal distribution, in contrast to MFGs or Schrödinger bridge approaches that use terminal costs. The flexibility of the regularization is argued to be crucial for practical DMT, especially in high-dimensional or multimodal settings.
Numerical Implementation via Gaussian Process PDEs
The paper presents a numerical algorithm for solving the control problem using Gaussian process (GP) methods for PDE-constrained optimization. Both the velocity potential u (with v=∇u) and the tilting function g are represented in RKHSs with separable kernels over space and time. The PDE constraints and boundary conditions are enforced at collocation points, and the optimization is performed via a penalized loss using Levenberg–Marquardt.
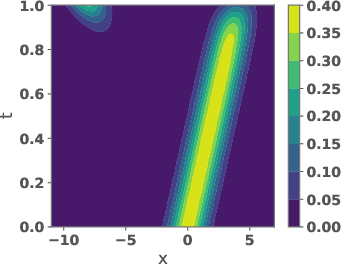
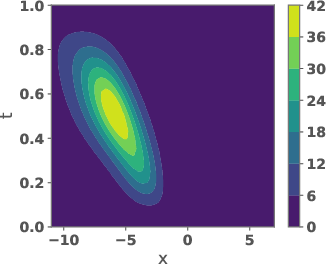
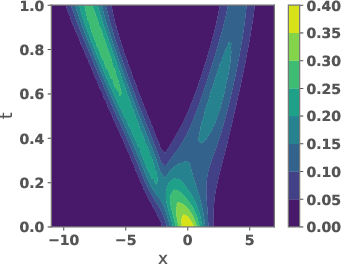
Figure 2: Space-time plots of the reference path μ(x,t), the tilting eg(x,t), and the learned path ρg(x,t).
The learned path eliminates the teleportation artifact present in the geometric path, resulting in more efficient and smoother transport dynamics. The velocity field vg associated with the learned path is shown to be spatially smoother and better aligned with the target distribution.
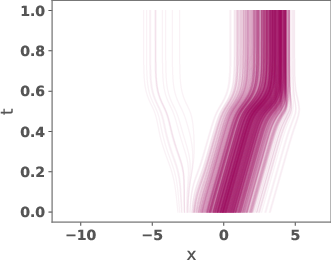
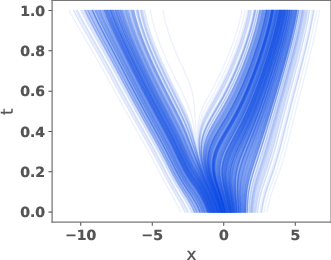
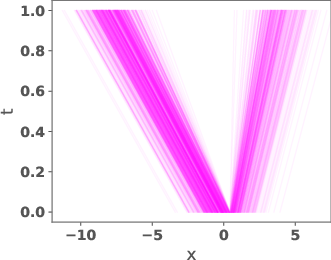
Figure 3: Trajectories for DMT between η and π using the reference velocity, learned velocity, and McCann interpolant velocity.
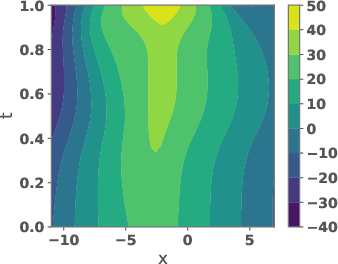
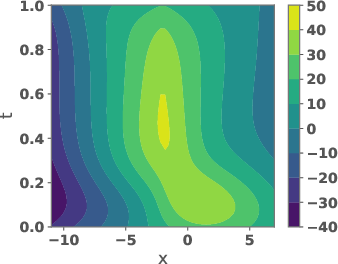
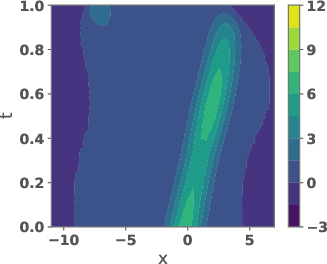
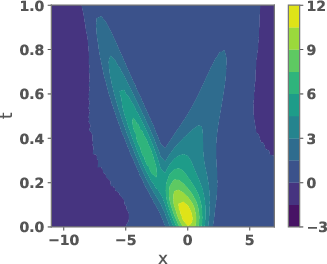
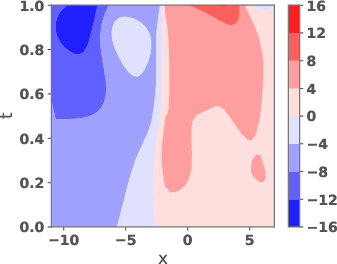
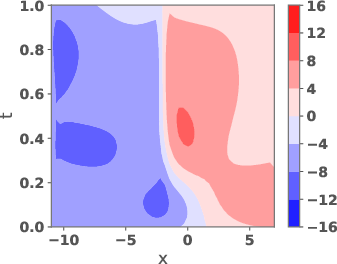
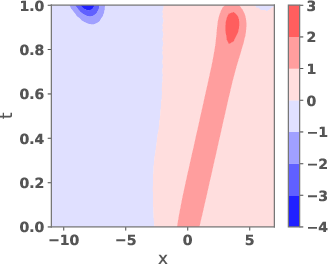
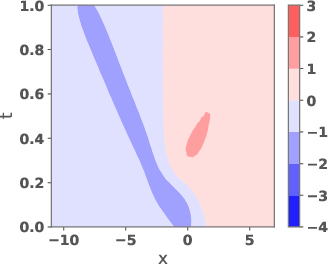
Figure 4: Potentials uref and ug and their weighted versions, as well as the corresponding velocity fields.
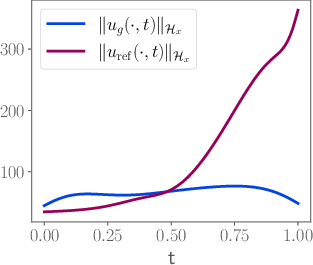
Figure 5: Spatial RKHS norms of ug(⋅,t) (blue) and uref(⋅,t) (red) as a function of time.
The spatial RKHS norm of the reference velocity increases sharply during the teleportation phase, while the learned velocity maintains a relatively constant norm, indicating improved regularity.
The paper provides quantitative metrics comparing the learned and reference interpolations:
| Method |
Fraction in Left Mode |
Rel. Error Mean ↓ |
Rel. Error Var ↓ |
MMD ↓ |
∥u∥H |
| Reference Interpolation |
0.005 |
1.80 |
0.96 |
0.743 |
770 |
| Learned Interpolation |
0.375 |
0.88 |
0.016 |
0.137 |
136 |
| Ground Truth Samples |
0.654 |
0.040 |
0.024 |
7.21×10−4 |
n/a |
The learned interpolation dramatically improves sample quality, especially in allocating mass to the correct mode and reducing the RKHS norm of the velocity.
Theoretical and Practical Implications
The control-theoretic framework for path identification in DMT provides a principled approach to regularizing transport dynamics, with direct implications for the design of efficient samplers in Bayesian inference, generative modeling, and data assimilation. The explicit connection to MFGs and the flexibility in regularization norms enable adaptation to problem-specific requirements, such as spatial and temporal smoothness.
The numerical results suggest that learned paths can significantly outperform canonical choices, especially in challenging multimodal scenarios. The GP-PDE approach is scalable and can be extended to higher dimensions and more complex reference/target pairs.
Future Directions
The paper outlines several avenues for future research, including:
- Exploration of alternative regularization penalties (e.g., Bochner space norms) to further control spatial and temporal regularity.
- Extension to stochastic dynamics and SDE-based DMT.
- Application to high-dimensional problems and real-world Bayesian inference tasks.
- Investigation of the interplay between path regularity and sample efficiency in practical settings.
Conclusion
This work introduces a general control-based framework for learning paths of measures in dynamic measure transport, emphasizing the importance of regularization for smooth and efficient sampling. The proposed approach, grounded in mean-field game theory and implemented via GP-PDE methods, demonstrates clear advantages over standard geometric annealing paths, both theoretically and empirically. The framework is broadly applicable and sets the stage for further advances in principled sampler design and probabilistic inference.




































