Into the Rabbit Hull: From Task-Relevant Concepts in DINO to Minkowski Geometry (2510.08638v1)

Abstract: DINOv2 is routinely deployed to recognize objects, scenes, and actions; yet the nature of what it perceives remains unknown. As a working baseline, we adopt the Linear Representation Hypothesis (LRH) and operationalize it using SAEs, producing a 32,000-unit dictionary that serves as the interpretability backbone of our study, which unfolds in three parts. In the first part, we analyze how different downstream tasks recruit concepts from our learned dictionary, revealing functional specialization: classification exploits "Elsewhere" concepts that fire everywhere except on target objects, implementing learned negations; segmentation relies on boundary detectors forming coherent subspaces; depth estimation draws on three distinct monocular depth cues matching visual neuroscience principles. Following these functional results, we analyze the geometry and statistics of the concepts learned by the SAE. We found that representations are partly dense rather than strictly sparse. The dictionary evolves toward greater coherence and departs from maximally orthogonal ideals (Grassmannian frames). Within an image, tokens occupy a low dimensional, locally connected set persisting after removing position. These signs suggest representations are organized beyond linear sparsity alone. Synthesizing these observations, we propose a refined view: tokens are formed by combining convex mixtures of archetypes (e.g., a rabbit among animals, brown among colors, fluffy among textures). This structure is grounded in Gardenfors' conceptual spaces and in the model's mechanism as multi-head attention produces sums of convex mixtures, defining regions bounded by archetypes. We introduce the Minkowski Representation Hypothesis (MRH) and examine its empirical signatures and implications for interpreting vision-transformer representations.

• The paper introduces the Minkowski Representation Hypothesis, showing that DINOv2 activations form convex mixtures of archetypes for improved interpretability.
• The paper details task-specific recruitment of concept families—such as Elsewhere, Border, and Depth cues—that align with classification, segmentation, and depth estimation tasks.
• The paper provides quantitative evidence of low-dimensional, coherent subspaces in token embeddings, supporting the non-linear geometric organization of representations.

Concept Geometry and Task Specialization in DINOv2: From Sparse Coding to Minkowski Representation

Introduction

This paper presents a comprehensive analysis of the internal representations of DINOv2, a self-supervised Vision Transformer, through the lens of concept extraction and geometric organization. The authors operationalize the Linear Representation Hypothesis (LRH) using large-scale sparse autoencoders (SAEs) to construct a 32,000-unit dictionary of visual concepts. The paper unfolds in three main parts: (1) functional specialization of concepts across downstream tasks, (2) statistical and geometric analysis of the learned concept dictionary, and (3) a theoretical and empirical proposal of the Minkowski Representation Hypothesis (MRH), which posits that activations are organized as convex mixtures of archetypes, forming Minkowski sums of polytopes rather than linear directions.

Figure 1: Overview of the paper, highlighting task-specific concept families, geometric and statistical properties of the learned dictionary, and the transition to Minkowski geometry for token representations.

Task-Specific Concept Recruitment

The analysis reveals that different downstream tasks—classification, segmentation, and depth estimation—recruit distinctive families of concepts from the learned dictionary. Classification tasks utilize "Elsewhere" concepts, which activate in regions excluding the object of interest but are causally dependent on its presence. Segmentation tasks rely on boundary concepts that consistently localize along object contours, forming coherent subspaces. Depth estimation tasks draw on three families of monocular cues: projective geometry, shadow-based cues, and frequency-based transitions, aligning with principles from visual neuroscience.

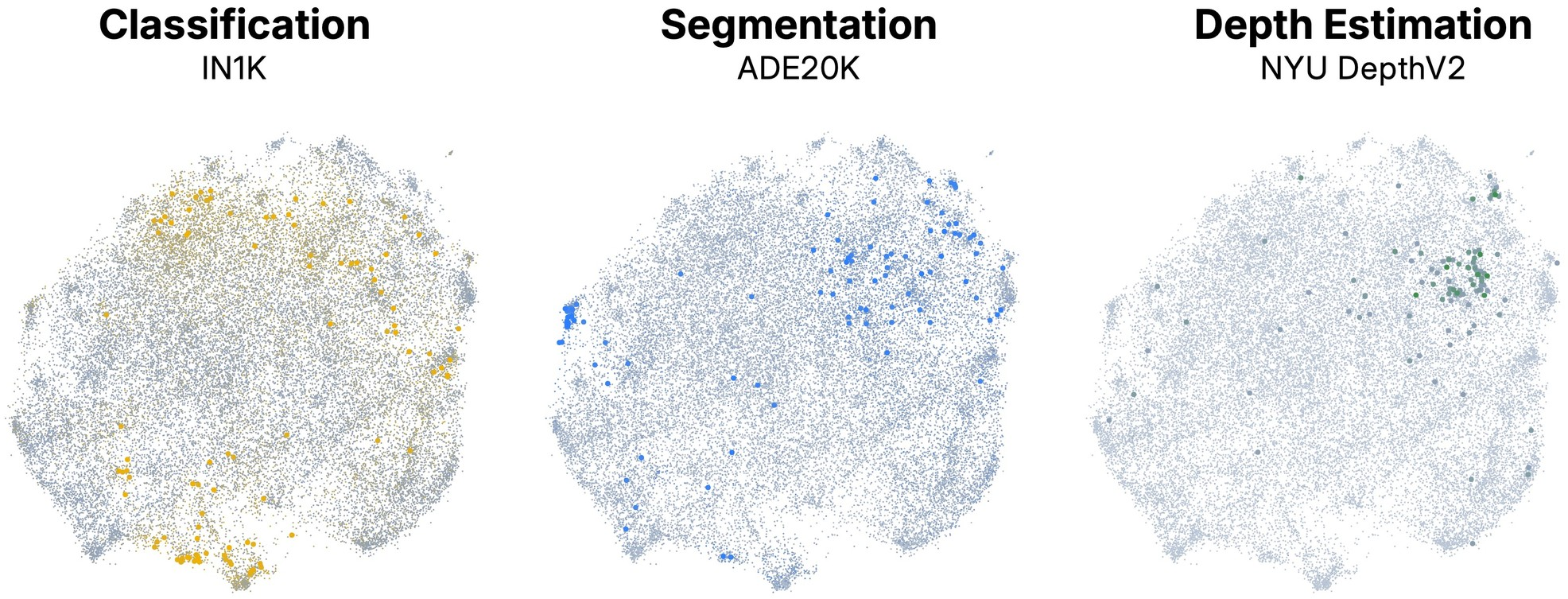
Figure 2: UMAP projection of the concept dictionary, colored by importance for classification, segmentation, and depth estimation, showing distinct functional clusters for each task.

Quantitative analysis demonstrates that classification tasks recruit a broader span of the dictionary, while segmentation and depth estimation activate more compact, low-dimensional regions. Intra-task concept pairs exhibit higher mutual alignment, and the singular value spectra of task-specific subspaces decay sharply, supporting the hypothesis that each task activates a low-dimensional functional subspace.

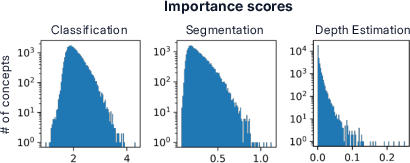
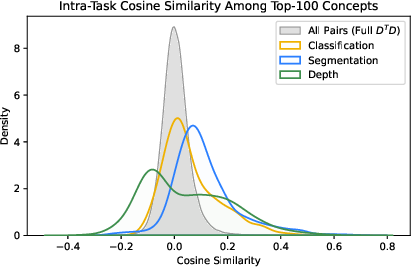
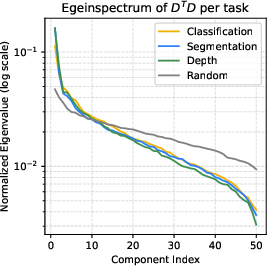
Figure 3: Classification recruits more concepts than segmentation or depth; intra-task concept similarity and spectral analysis reveal coherent, low-dimensional subspaces for each task.

Concept Families: Elsewhere, Border, and Depth Cues

"Elsewhere" concepts, central to classification, activate off-object regions but are causally linked to the presence of the object, implementing a form of learned negation and distributed spatial logic. Segmentation concepts are spatially localized along object boundaries, forming tight clusters in embedding space and supporting robust contour detection. Depth estimation concepts are organized into three interpretable clusters, each sensitive to specific image manipulations, indicating that DINOv2 encodes a rich basis of 3D perception primitives from 2D data.

Figure 4: Visualization of "Elsewhere" concepts, showing off-object activation conditioned on object presence across multiple ImageNet classes.

Figure 5: Segmentation concepts activate along object boundaries, forming a low-dimensional submanifold in concept space.

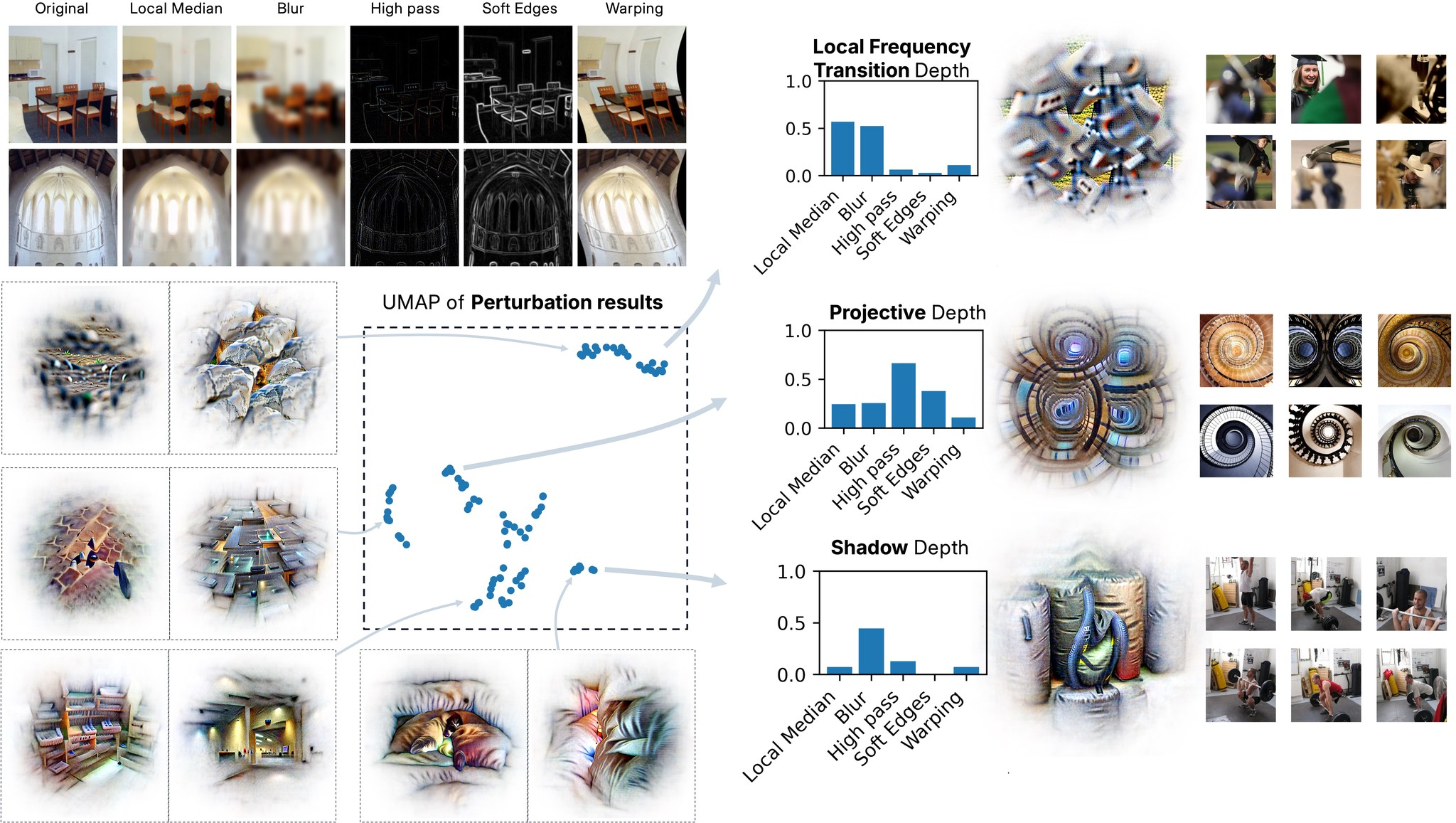
Figure 6: Depth estimation concepts cluster into projective geometry, shadow-based, and frequency-based families, supporting monocular depth reasoning.

Token-Type-Specific Concepts and Global Scene Properties

The paper identifies token-type-specific concepts, with a significant subset exhibiting strong localization. While most concepts are positionally agnostic, hundreds activate exclusively on register tokens, encoding global scene properties such as illumination, motion blur, and lens effects. This specialization suggests that register tokens serve as conduits for abstract, non-local information, distinct from spatial or object-centric features.

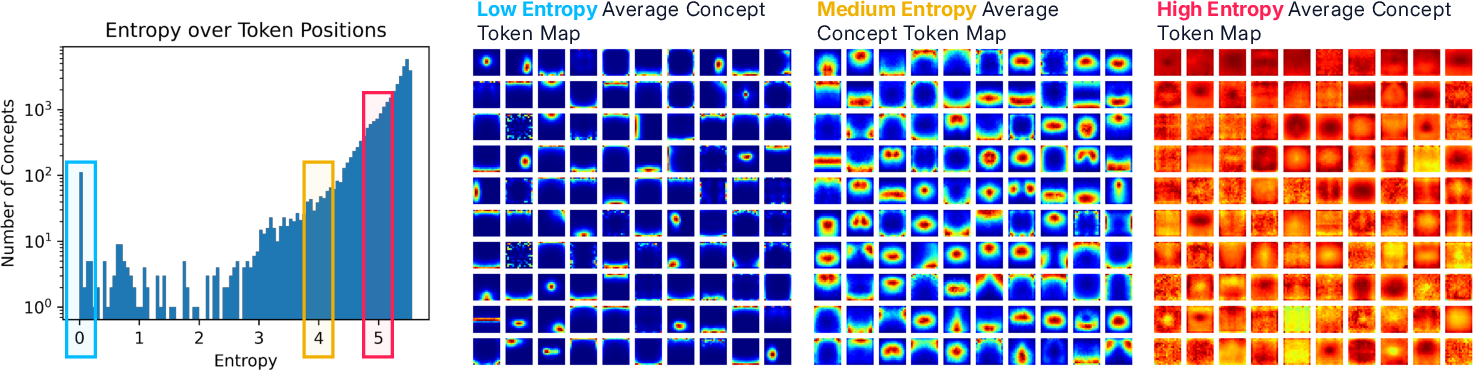
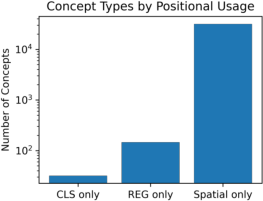
Figure 7: Distribution of concept entropy across token positions, revealing both localized and positionally agnostic concepts.

Figure 8: Register-only concepts encode global scene properties, such as lighting and motion blur, distinct from object or region-specific features.

Statistical and Geometric Organization of Concepts

The concept dictionary exhibits a hybrid regime: most features are sparse and selective, but a few outlier concepts encode dense, dataset-wide positional information. The co-activation Gram matrix displays a smooth eigenvalue decay, indicating a high-dimensional, distributed regime without clear modularity. Geometric analysis shows that the dictionary departs from the ideal of a uniformly incoherent Grassmannian frame, exhibiting higher coherence, clustered structure, and antipodal pairs that encode semantically opposed features.

Figure 9: Pairwise inner product distribution, singular value spectrum, and Hoyer sparsity scores for the concept dictionary, revealing higher coherence and anisotropy than random or Grassmannian baselines.

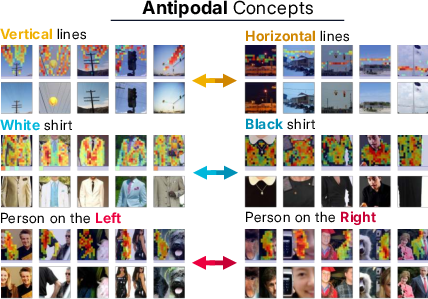
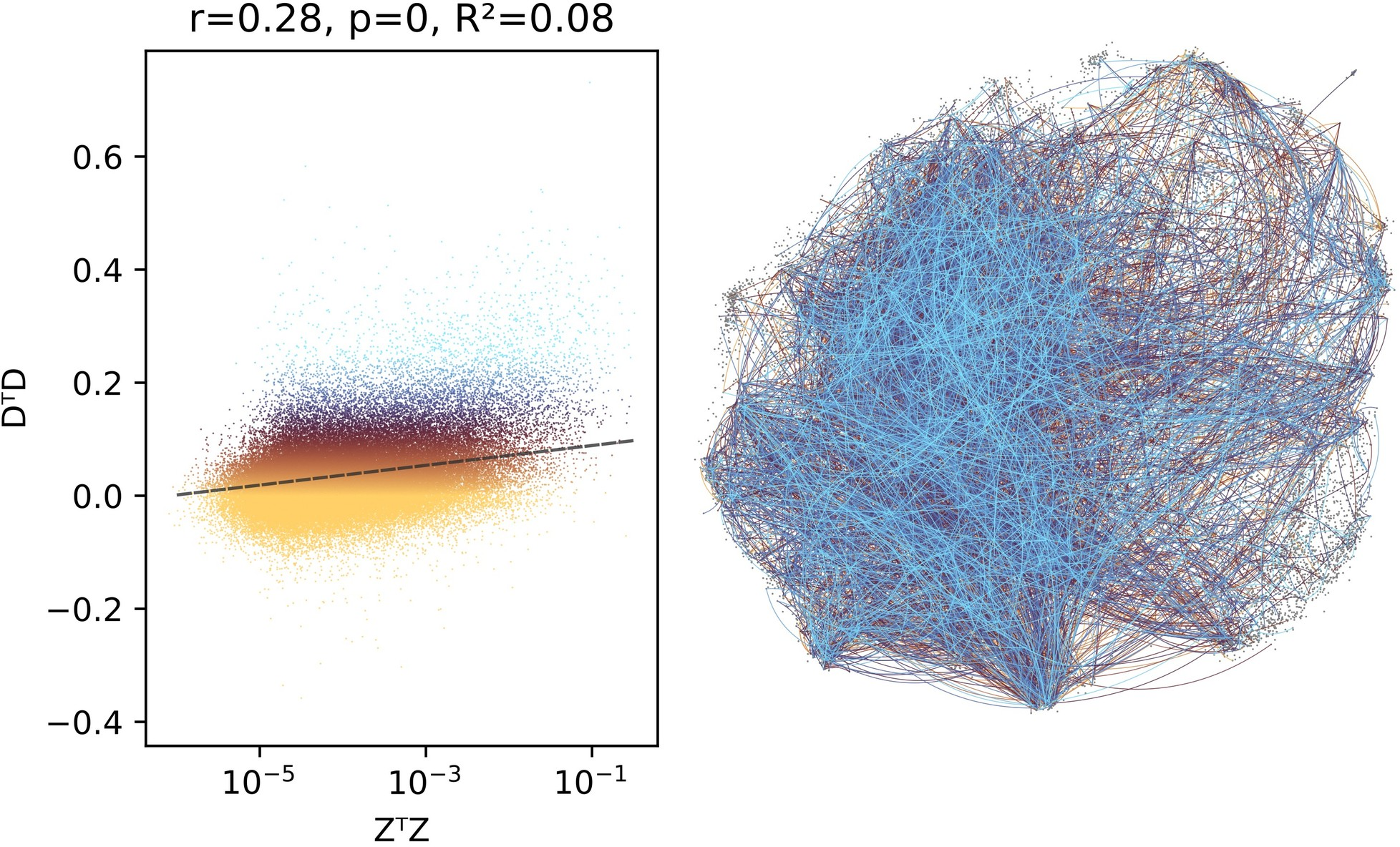
Figure 10: Antipodal concept pairs and weak correlation between co-activation and geometric similarity, indicating non-local, non-modular organization.

Local Embedding Geometry and Positional Compression

Within single images, patch tokens occupy smooth, low-dimensional manifolds in embedding space, with transitions aligned to object boundaries. Positional information compresses over layers, converging to a 2D subspace in the final layers, but local connectedness persists even after removing positional components, indicating deeper geometric organization beyond position alone.

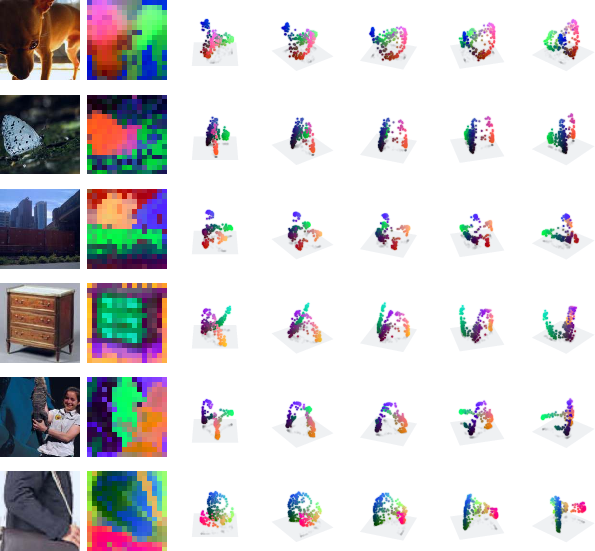
Figure 11: PCA projections of patch embeddings reveal smooth, locally connected manifolds aligned with perceptual contours.

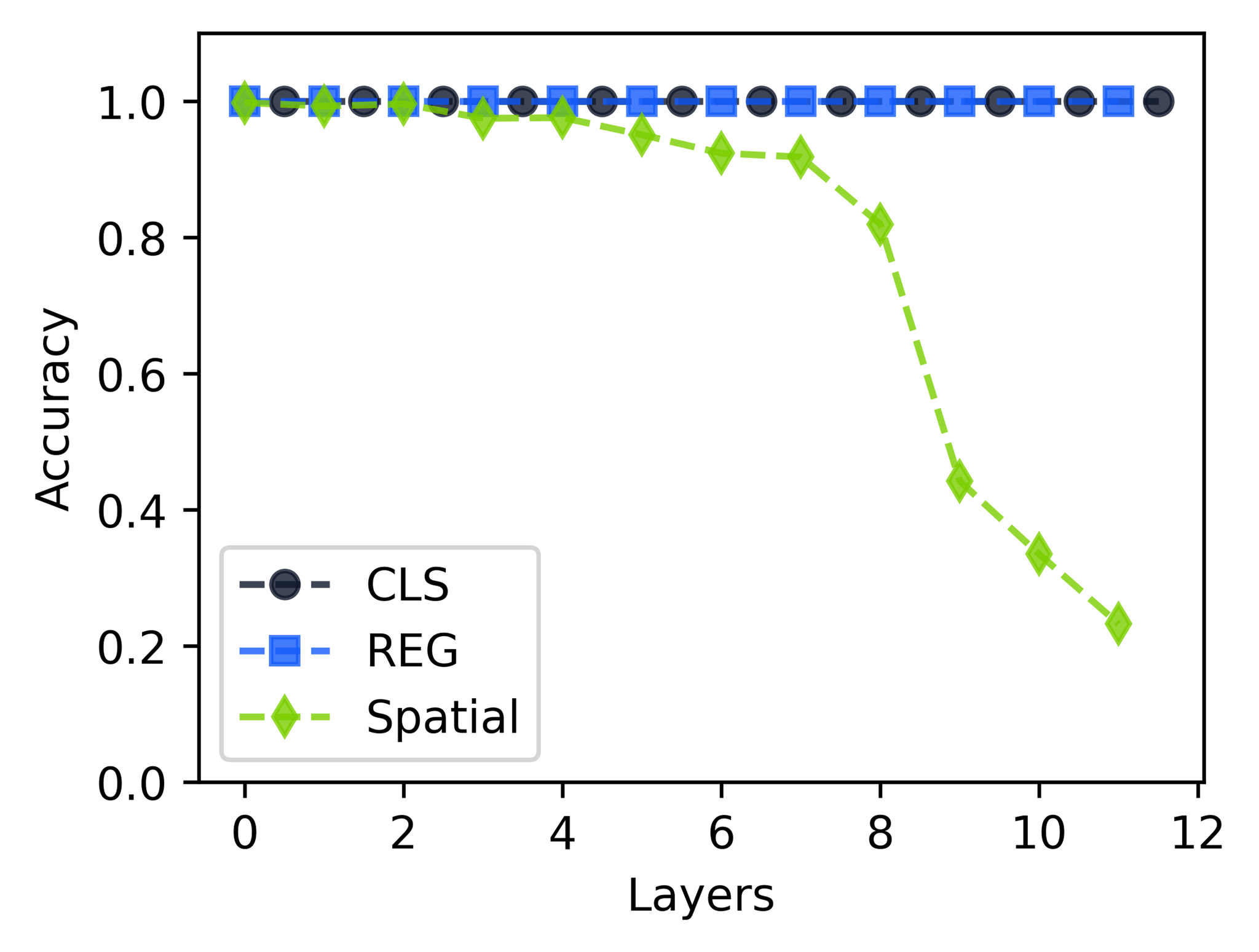
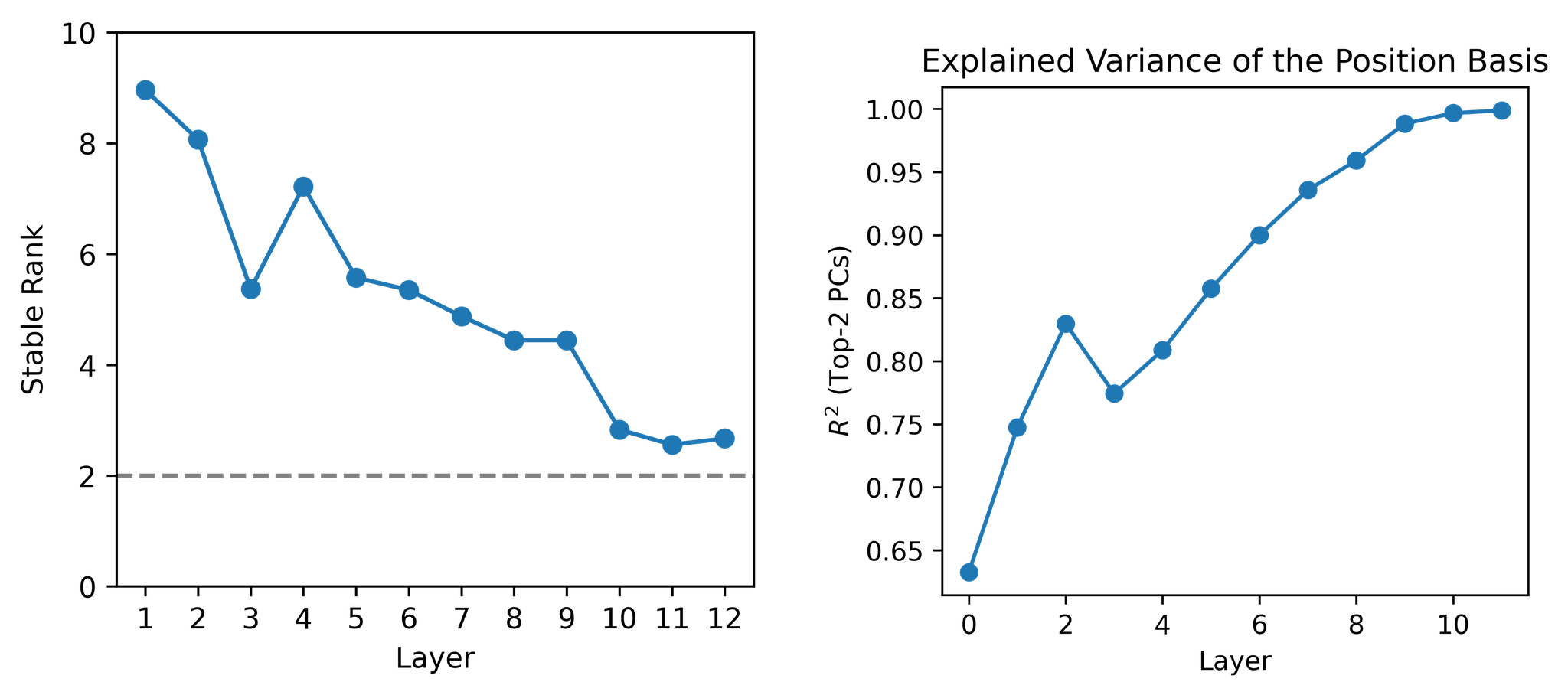
Figure 12: Positional encoding compresses to a 2D sheet over layers; PCA components explain variance beyond position, supporting intrinsic geometric structure.

Minkowski Representation Hypothesis

Synthesizing these observations, the authors propose the Minkowski Representation Hypothesis (MRH): activations are formed as convex mixtures of archetypes, and the activation space is a Minkowski sum of convex polytopes. This structure is theoretically grounded in Gärdenfors' conceptual spaces and is naturally implemented by multi-head attention, where each head produces convex combinations of value vectors and their outputs add across heads.

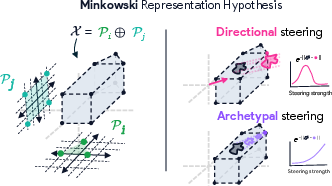
Figure 13: Schematic of MRH, showing activation space as a Minkowski sum of polytopes formed by archetypal points; steering along directions quickly leaves the manifold, while archetypal steering remains within valid regions.

Empirical evidence supports MRH: piecewise-linear geodesics on token k-NN graphs remain close to the data manifold, archetypal analysis achieves low reconstruction error with few archetypes, and archetypal coefficient matrices reveal emergent block structure. The MRH implies that concepts are best understood as landmarks or convex regions, steering admits strict identifiable maxima, and decomposition is fundamentally non-identifiable without access to intermediate representations.

Figure 14: Empirical support for MRH: piecewise-linear paths remain close to the data manifold, archetypal analysis matches SAE performance with few archetypes, and block-structured co-activation emerges naturally.

Implications and Future Directions

The findings have significant implications for interpretability and model analysis. If MRH holds, concept extraction cannot rely solely on layer activations; meaningful structure must be recovered through the sequence of transformations that formed the representation. The non-identifiability of Minkowski decomposition suggests that interpretability methods should exploit architectural structure, such as attention weights and intermediate activations, rather than treating learned representations as opaque geometric objects.

Conclusion

This work presents a large-scale concept analysis of DINOv2, revealing functional specialization, hybrid sparse-dense organization, and geometric structure beyond linear sparsity. The Minkowski Representation Hypothesis offers a refined view of token representations as convex mixtures of archetypes, with theoretical and empirical support. These insights motivate the development of structure-aware interpretability techniques and suggest new directions for understanding and steering vision transformer representations.