AMAQ: Adaptive Mixed-bit Activation Quantization for Collaborative Parameter Efficient Fine-tuning (2510.05468v1)

Abstract: LLMs are scaling rapidly, creating significant challenges for collaborative server client distributed training, particularly in terms of communication efficiency and computational overheads. To address these challenges, we implement Parameter-efficient Split Learning, which effectively balances efficiency and performance for collaborative training on low-resource devices. To reduce communication overhead in collaborative training, we introduce Adaptive Mixed bit Activation Quantization (AMAQ), a strategy that progressively compresses activations and gradients from high precision (6 to 8 bits) to low precision (3 to 4 bits). AMAQ achieves this by effectively allocating bit budgets across channels based on feature wise and layer wise importance using bit regularization. Under the same bit budgets, AMAQ outperforms fixed-precision approaches, delivering about 2.5% higher generation accuracy and about 1.3% better classification accuracy for models like LLaMA3 8B and Qwen2.5 7B. In addition, it significantly enhances training stability and reducing ultra-low bit representation collapse during the training. Experiments demonstrate that AMAQ integrates effectively into practical multi-machine collaborative training setups, offering superior inference accuracy with only a modest communication overhead for bits adaptation during training. This trade off makes AMAQ a practical and effective solution for collaborative training with minimal communication cost.

• The paper introduces AMAQ, a framework that dynamically allocates mixed-bit quantization to activations, balancing communication costs with model performance.
• It leverages a learnable gating parameter and a gradual quantization schedule to maintain stability and achieve high accuracy on benchmarks.
• The approach significantly reduces activation transmission—up to 4–5×—making it effective for resource-constrained, distributed training environments.

Adaptive Mixed-bit Activation Quantization for Collaborative Parameter Efficient Fine-tuning

Introduction and Motivation

The exponential scaling of LLMs has exacerbated the computational and communication bottlenecks in collaborative server-client distributed training, especially for resource-constrained devices. While PEFT methods such as LoRA, adapters, and prompt tuning have reduced the number of trainable parameters, the transmission of intermediate activations in split learning remains a major source of communication overhead. The "AMAQ: Adaptive Mixed-bit Activation Quantization for Collaborative Parameter Efficient Fine-tuning" (2510.05468) paper introduces AMAQ, a quantization-aware training framework that adaptively compresses activations and gradients by dynamically allocating bit-widths per channel and layer, thereby optimizing the trade-off between communication cost and model performance.

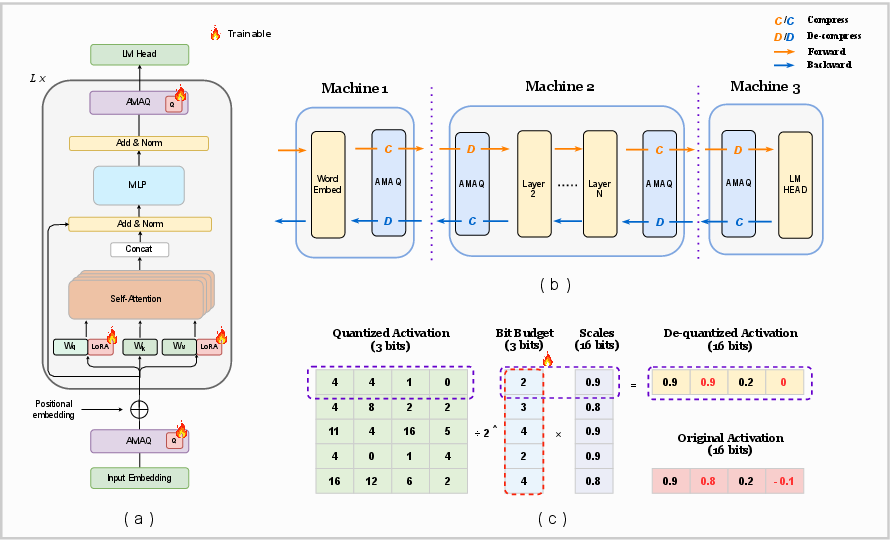
Figure 1: (a) AMAQ pipeline with joint optimization of LoRA and quantization parameters; (b) Split learning deployment with activation compression; (c) Visualization of dequantized activations and dynamic bit allocation.

Methodology

Adaptive Mixed-bit Activation Quantization

AMAQ leverages a learnable gating parameter $Q$ for each activation channel, modulated by a sigmoid function and scaling coefficient $\alpha$, to control the effective bit-width:

$$\text{Bit-width} = \text{min} + (\text{max} - \text{min}) \times \sigma(\alpha Q)$$

$Q$ is optimized independently from model and LoRA weights, allowing fine-grained control over quantization granularity. The quantization schedule transitions from high to low precision during training, mitigating abrupt representational collapse and maintaining stability. The framework employs STE to enable gradient flow through non-differentiable quantization operations.

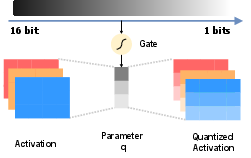
Figure 2: AMAQ gating mechanism for per-channel bit-width adaptation.

Bit Regularization and Loss Clipping

To regularize the bit allocation, AMAQ introduces an L2 (or optionally L1) penalty on the gating parameters, forming a composite loss:

$$\text{Loss} = \text{QAT\_Loss} + \beta \times \text{Bits\_Loss}$$

A clipping function constrains the mean bit-width to the target, preserving inter-channel importance and preventing over-quantization. This is critical for maintaining performance, especially when the quantization schedule is aggressive.

Experimental Results

Generation and Classification Performance

AMAQ is evaluated on LLaMA3-8B, Qwen2.5-7B/14B, and Phi-3-Medium across GSM8K, MATH, CodeAlpaca, BoolQ, ARC-C, Winogrande, and CommonsenseQA. Under identical bit budgets, AMAQ consistently outperforms fixed-precision and stochastic quantization baselines (AQ-SGD, QAT-Group, Channel-Wise, Tensor-Wise), with up to 2.5% higher generation accuracy and 1.3% better classification accuracy. Notably, AMAQ maintains stability and mitigates ultra-low bit collapse at 3–4 bits, where other methods exhibit significant degradation.

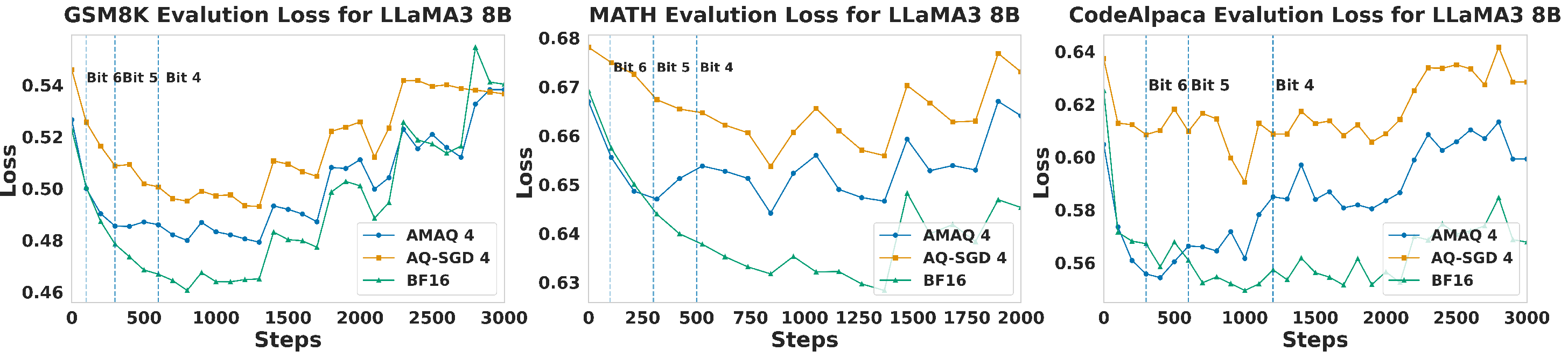
Figure 3: Loss curves for AMAQ vs. AQ-SGD and BF16 across benchmarks and bit-widths.

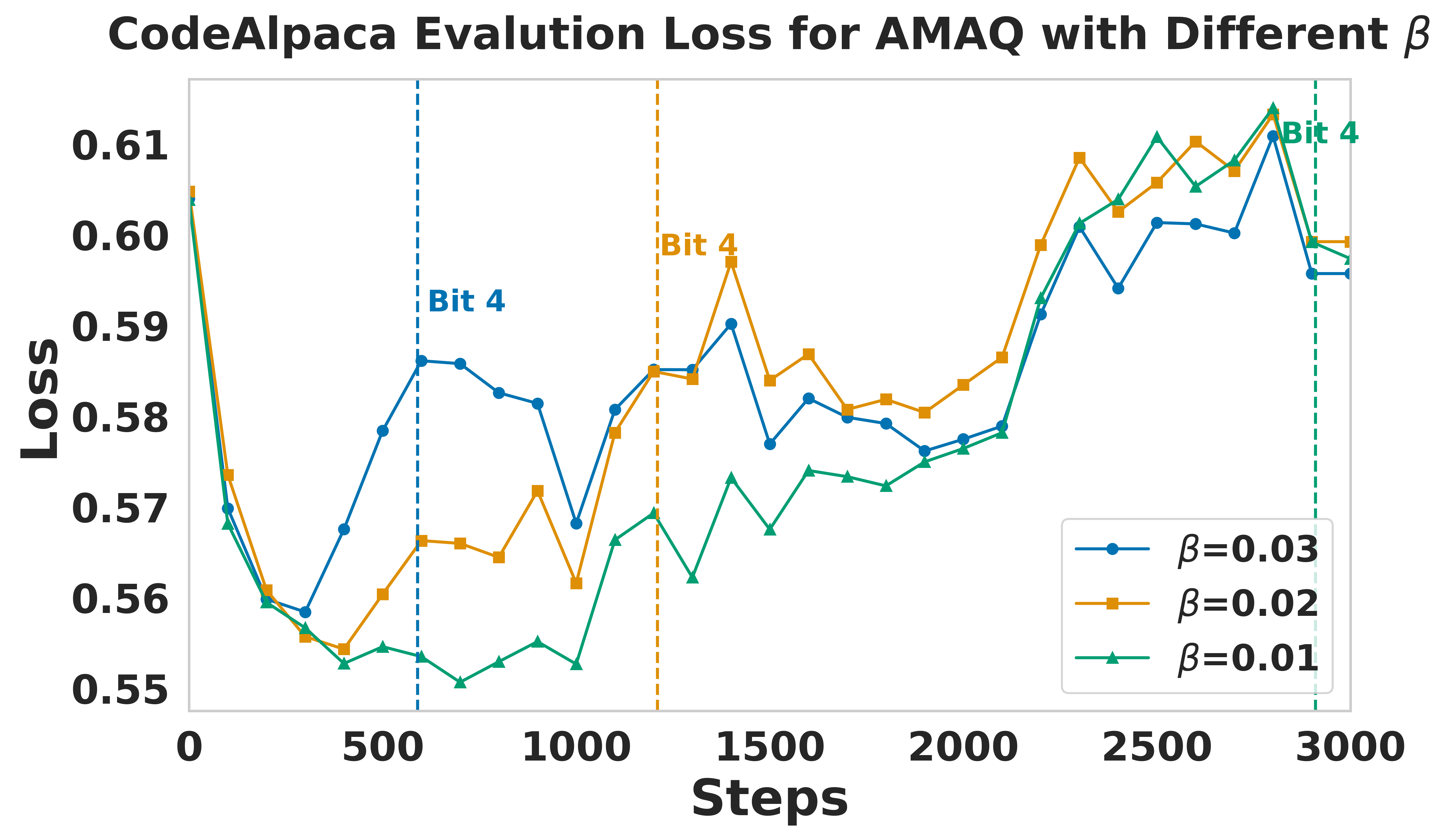
Figure 4: CodeAlpaca performance sensitivity to $\beta$ regularization parameter.

Split Learning and Communication Efficiency

In multi-machine split learning setups, AMAQ reduces activation transmission size by 4–5$\times$ compared to BF16, with only a modest increase in communication overhead for bit adaptation. The framework supports both LoRA-only and full-layer quantization, demonstrating practical deployment feasibility on heterogeneous hardware.

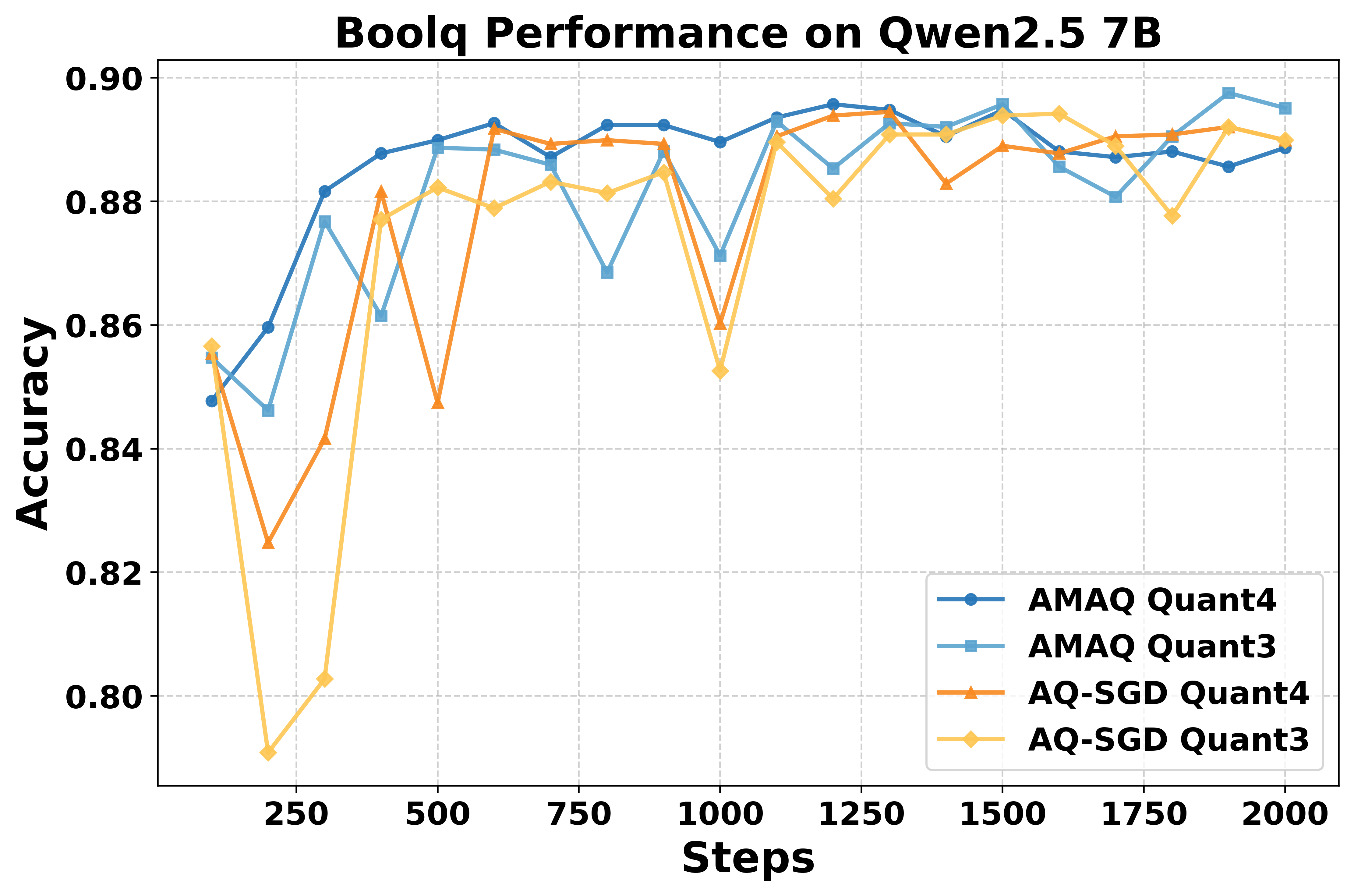
Figure 5: Qwen2.5-7B stability on BoolQ under input/output activation quantization.

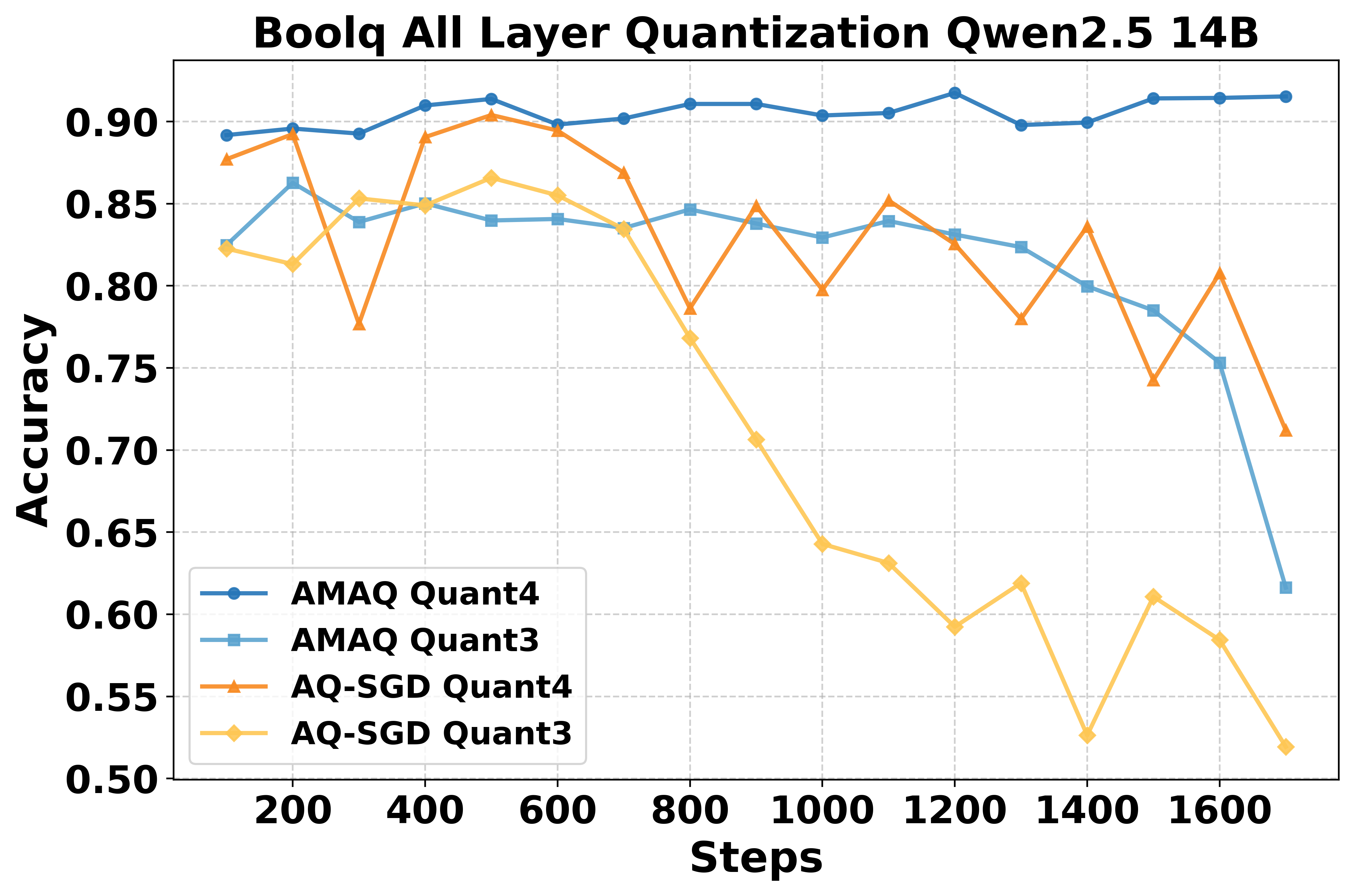
Figure 6: Qwen2.5-14B stability on BoolQ under full-layer quantization.

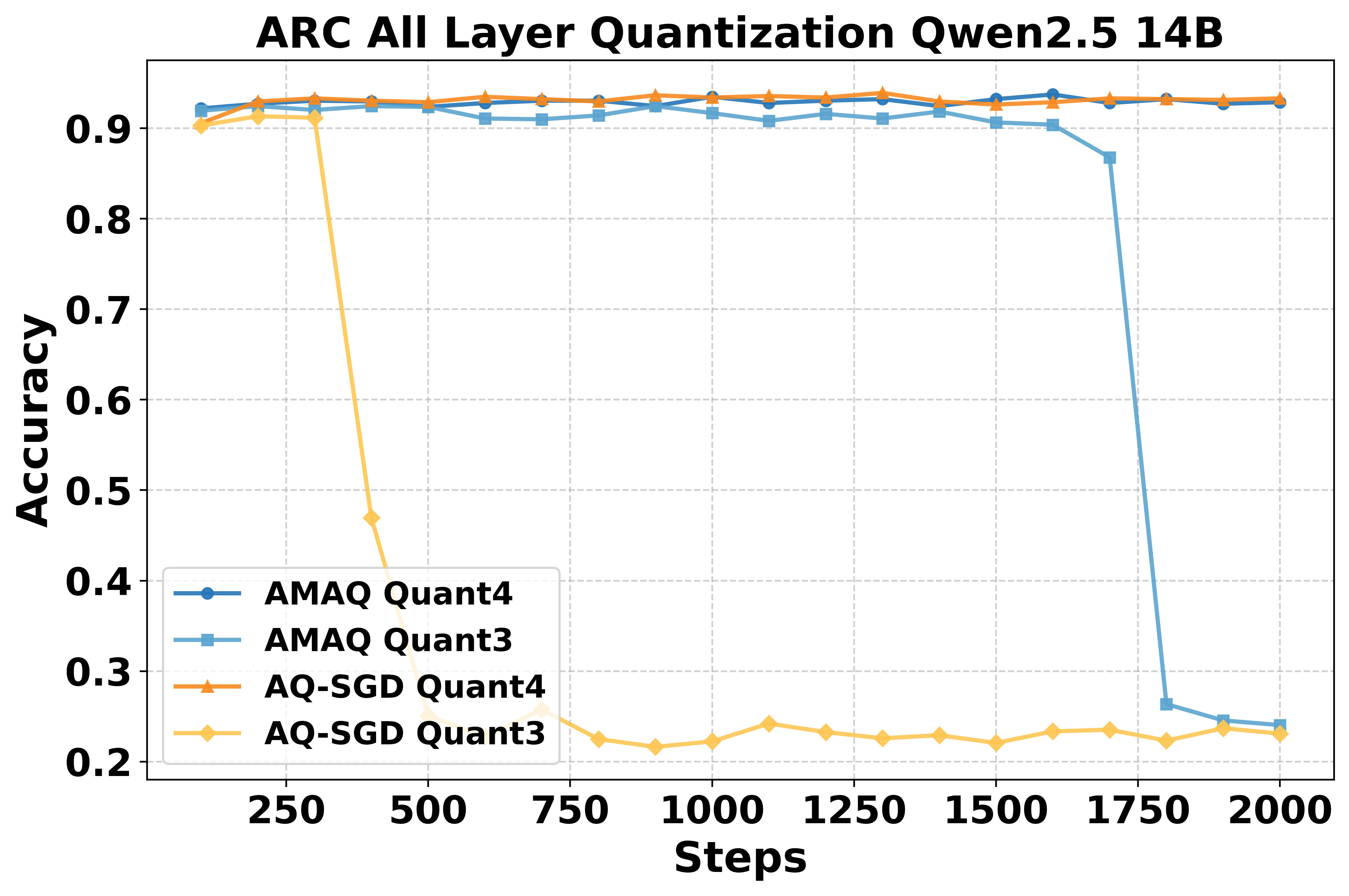
Figure 7: Qwen2.5-14B stability on ARC under full-layer quantization.

Robustness and Hyperparameter Sensitivity

AMAQ's stability is superior to AQ-SGD, especially at 3-bit quantization, where AQ-SGD often diverges. The adaptation speed to target bit-width is governed by $\beta$ and the learning rate of $Q$; aggressive schedules can induce instability, necessitating careful tuning. The output layers generally require higher bit-widths than input layers, reflecting asymmetric sensitivity to quantization.

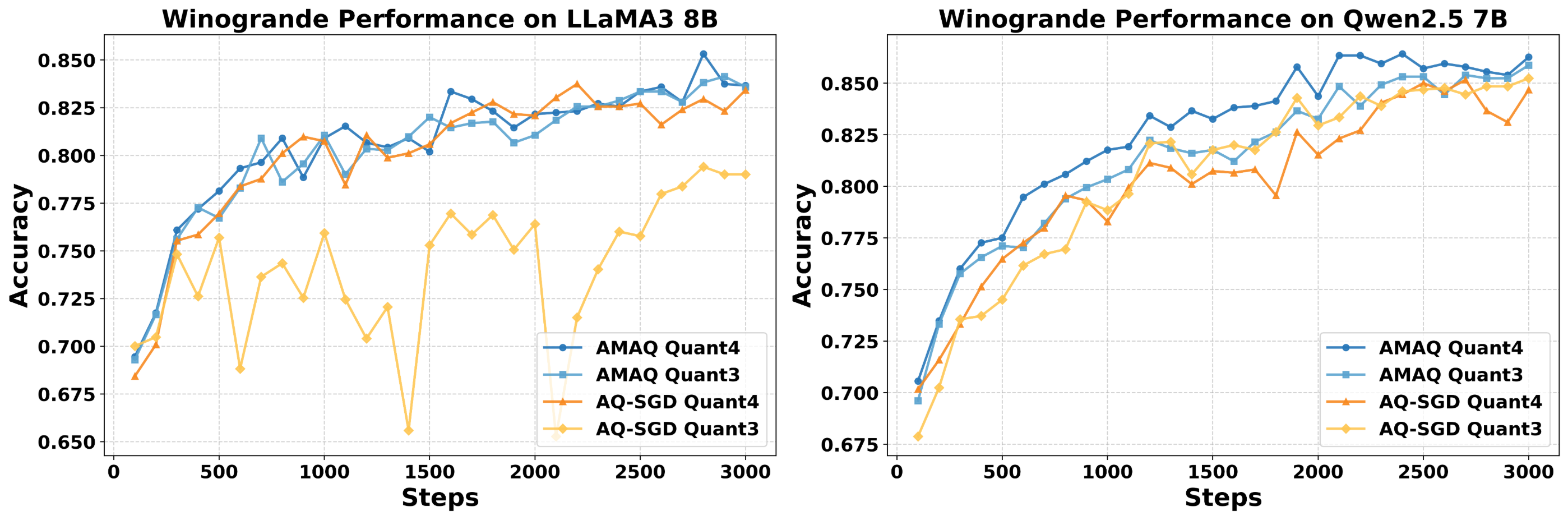
Figure 8: Winogrande performance for LLaMA3 8B and Qwen2.5 7B under varying bit-widths.

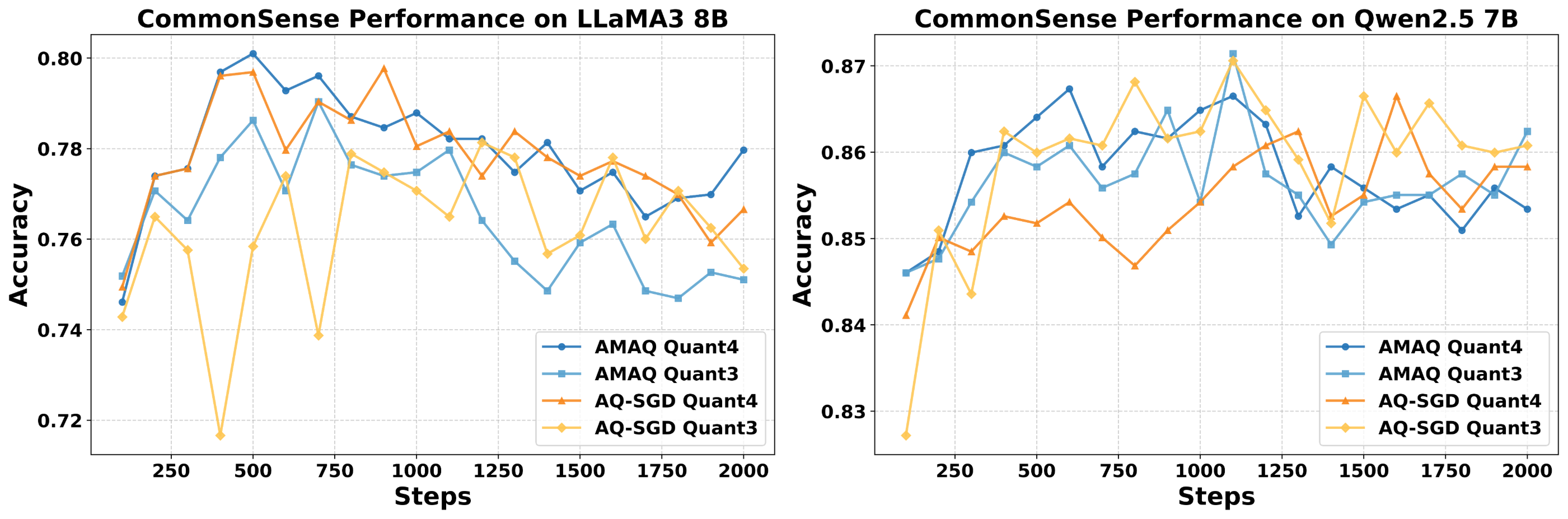
Figure 9: CommonsenseQA performance for LLaMA3 8B and Qwen2.5-7B under varying bit-widths.

Implementation Considerations

Integration and Deployment

AMAQ is implemented in PyTorch, leveraging distributed training primitives for split learning. The quantizer module is inserted at activation boundaries, with $Q$ parameters registered as a separate optimizer group. For LoRA-based PEFT, AMAQ is applied to activations at the input embedding and output LM head; for full fine-tuning, it is extended to all transformer layers. The bit regularization and clipping are integrated into the training loop, with hyperparameters ($\beta$, initial bit-width, learning rates) tuned per task.

Resource and Scaling

AMAQ introduces negligible computational overhead for bit adaptation, with the main cost being the additional optimizer step for $Q$. Communication savings are substantial, especially in bandwidth-constrained environments. The method scales to large models (14B parameters) and supports both single- and multi-machine deployments.

Limitations

AMAQ's effectiveness is contingent on the convergence rate of the underlying task; rapid overfitting can preclude full bit adaptation. Hyperparameter sensitivity remains a challenge, requiring robust tuning strategies. The method is most effective when the quantization schedule is aligned with the training dynamics.

Theoretical and Practical Implications

AMAQ advances the state-of-the-art in activation quantization for collaborative LLM training, demonstrating that adaptive, feature-wise bit allocation can preserve performance under stringent communication constraints. The framework is extensible to federated and privacy-preserving settings, where activation compression is critical. The dynamic quantization paradigm may inform future research in mixed-precision training, efficient inference, and secure model deployment.

Future Directions

Potential avenues include multi-party collaborative training, automated hyperparameter optimization for bit adaptation, and extension to KV cache quantization for efficient inference. Further exploration of privacy-utility trade-offs via differential privacy and mutual information analysis is warranted.

Conclusion

AMAQ provides a robust, adaptive solution for activation quantization in distributed, parameter-efficient LLM fine-tuning. By dynamically allocating bit-widths based on feature and layer importance, it achieves superior performance and stability compared to fixed-precision baselines, with significant communication savings. The framework is practical for real-world deployment and sets a foundation for future research in efficient, collaborative model training.