Detecting Invariant Manifolds in ReLU-Based RNNs (2510.03814v2)

Abstract: Recurrent Neural Networks (RNNs) have found widespread applications in machine learning for time series prediction and dynamical systems reconstruction, and experienced a recent renaissance with improved training algorithms and architectural designs. Understanding why and how trained RNNs produce their behavior is important for scientific and medical applications, and explainable AI more generally. An RNN's dynamical repertoire depends on the topological and geometrical properties of its state space. Stable and unstable manifolds of periodic points play a particularly important role: They dissect a dynamical system's state space into different basins of attraction, and their intersections lead to chaotic dynamics with fractal geometry. Here we introduce a novel algorithm for detecting these manifolds, with a focus on piecewise-linear RNNs (PLRNNs) employing rectified linear units (ReLUs) as their activation function. We demonstrate how the algorithm can be used to trace the boundaries between different basins of attraction, and hence to characterize multistability, a computationally important property. We further show its utility in finding so-called homoclinic points, the intersections between stable and unstable manifolds, and thus establish the existence of chaos in PLRNNs. Finally we show for an empirical example, electrophysiological recordings from a cortical neuron, how insights into the underlying dynamics could be gained through our method.

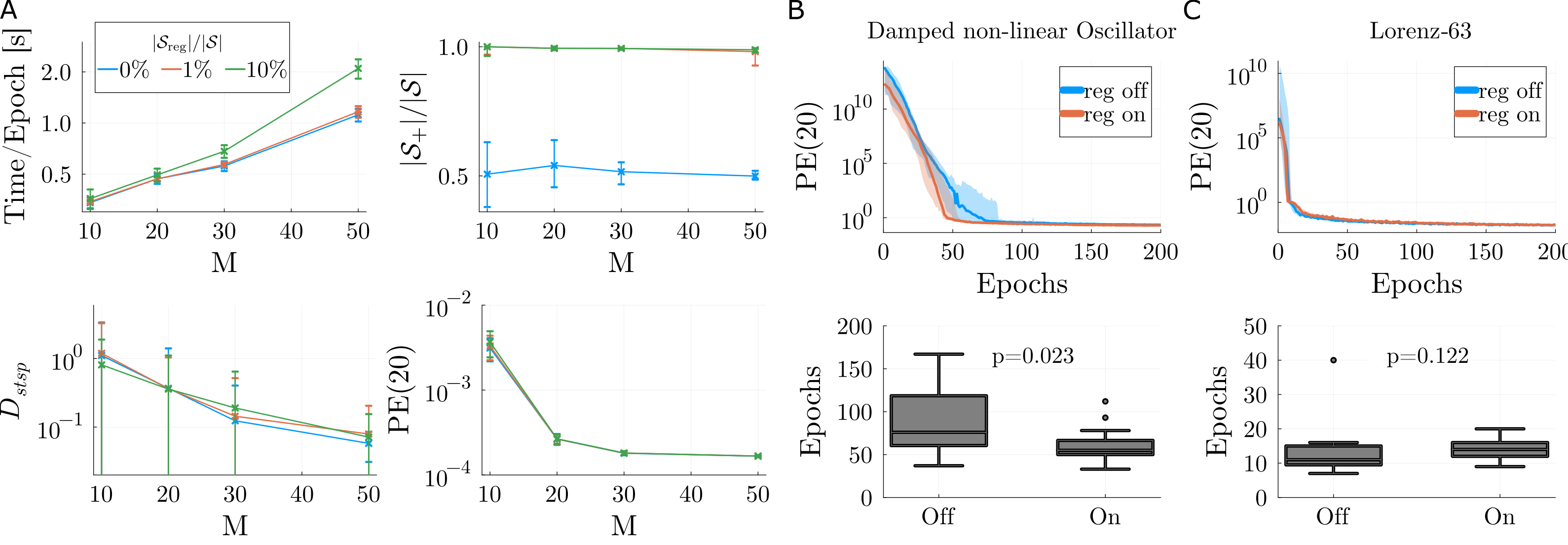
• The paper presents a novel algorithm that initializes, propagates, and segments manifold trajectories using eigenvectors to detect stable and unstable invariant manifolds in ReLU-based RNNs.
• The approach accurately distinguishes linear subregions to identify bifurcations, homogeneous foldings, and homoclinic points that signal multistability and chaos.
• The methodology has practical applications in neuroscience and time series prediction by mapping neural attractor states and improving model interpretability.

Detecting Invariant Manifolds in ReLU-Based RNNs

In the paper "Detecting Invariant Manifolds in ReLU-Based RNNs" (2510.03814), the authors introduce a novel algorithm designed to detect invariant manifolds in piecewise-linear RNNs using ReLU as their activation function. The approach primarily focuses on identifying stable and unstable manifolds, segments that delineate different basins of attraction and contribute to the dynamical behavior of a neural network. This methodology not only supports the detection of multistability, a pivotal characteristic in neural computation, but also identifies homoclinic points indicating chaos within these models.

Algorithm Overview

Manifold Detection Strategy

The algorithm exploits the piecewise-linear structure inherent in ReLU-based RNNs. Starting with known fixed or cyclic points determined using the SCYFI algorithm, it systematically traces out stable and unstable manifolds:

1. Initialization: The stable or unstable manifold is initialized using eigenvectors associated with either stable or unstable eigenvalues of the fixed or cyclic point's local Jacobian.
2. Propagation: Seed points along these eigenvectors are propagated through linear subregions associated with the piecewise-linear structure, updating their positions using forward and backward iterations.
3. Segmentation: As the trajectory crosses into new linear subregions, it is adjusted to adhere to the new region's dynamics, either by maintaining a planar segment or acquiring curvature as dictated by eigenvalue characteristics.

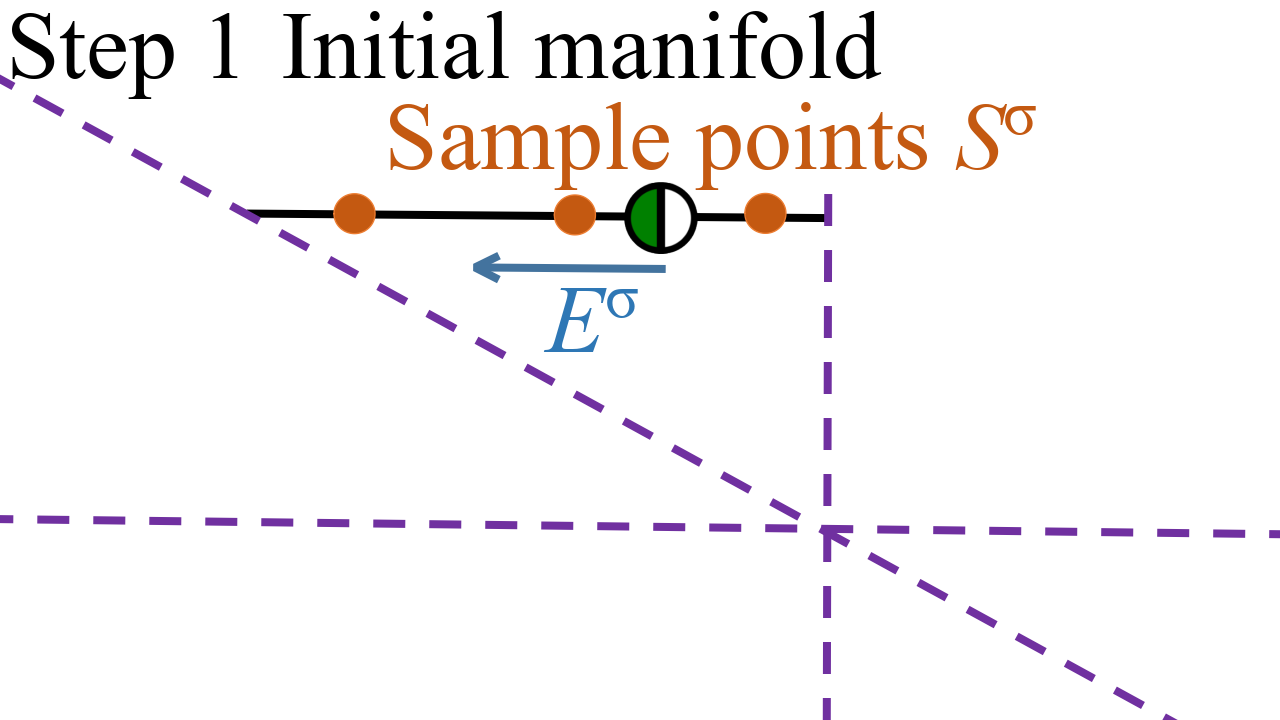
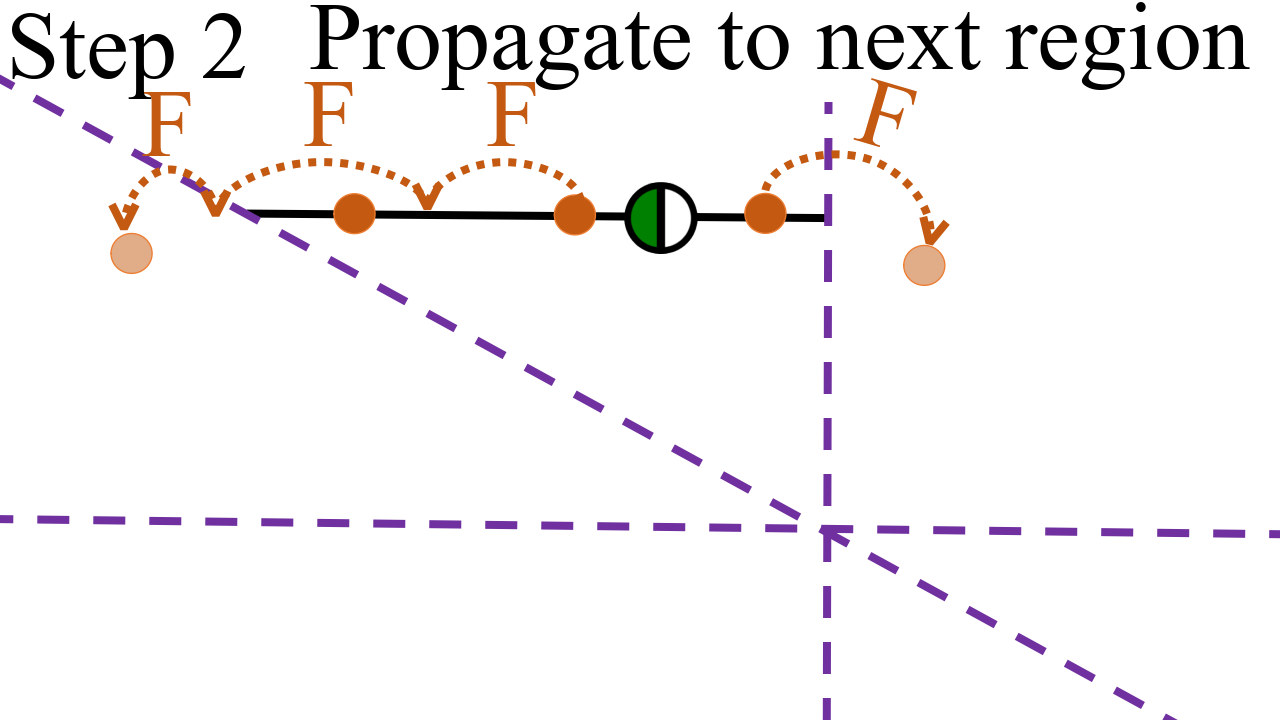
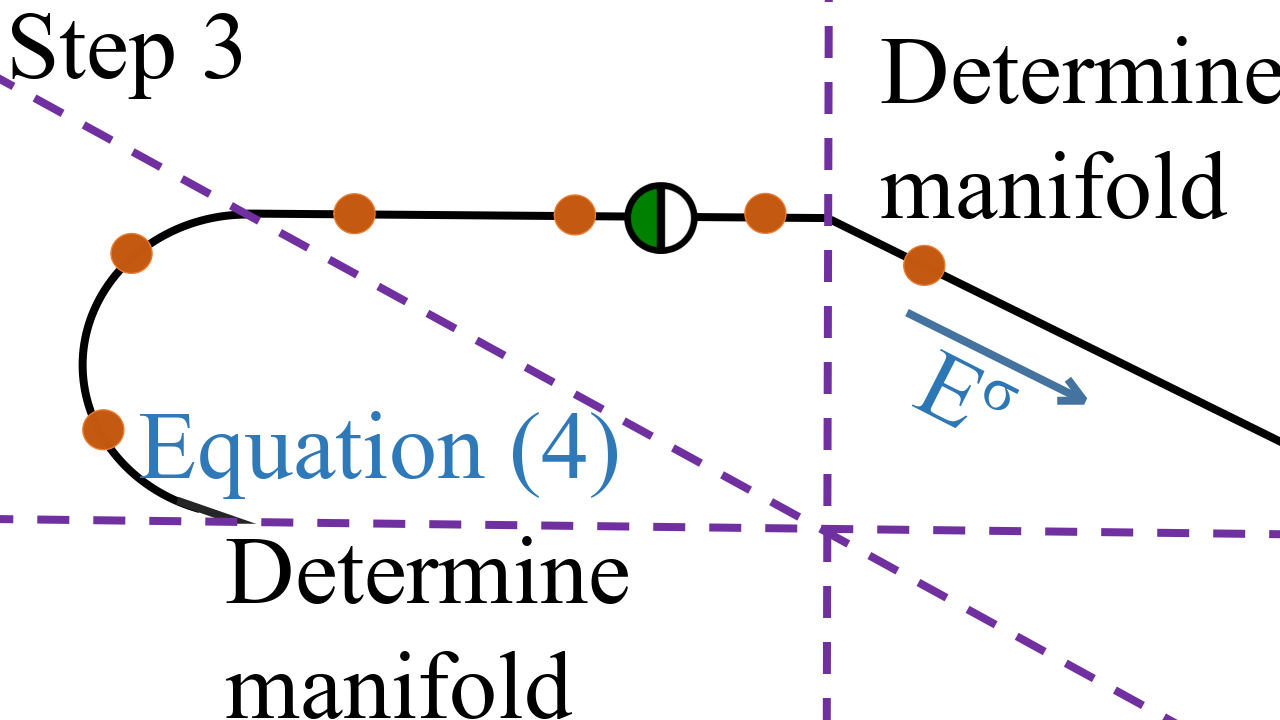
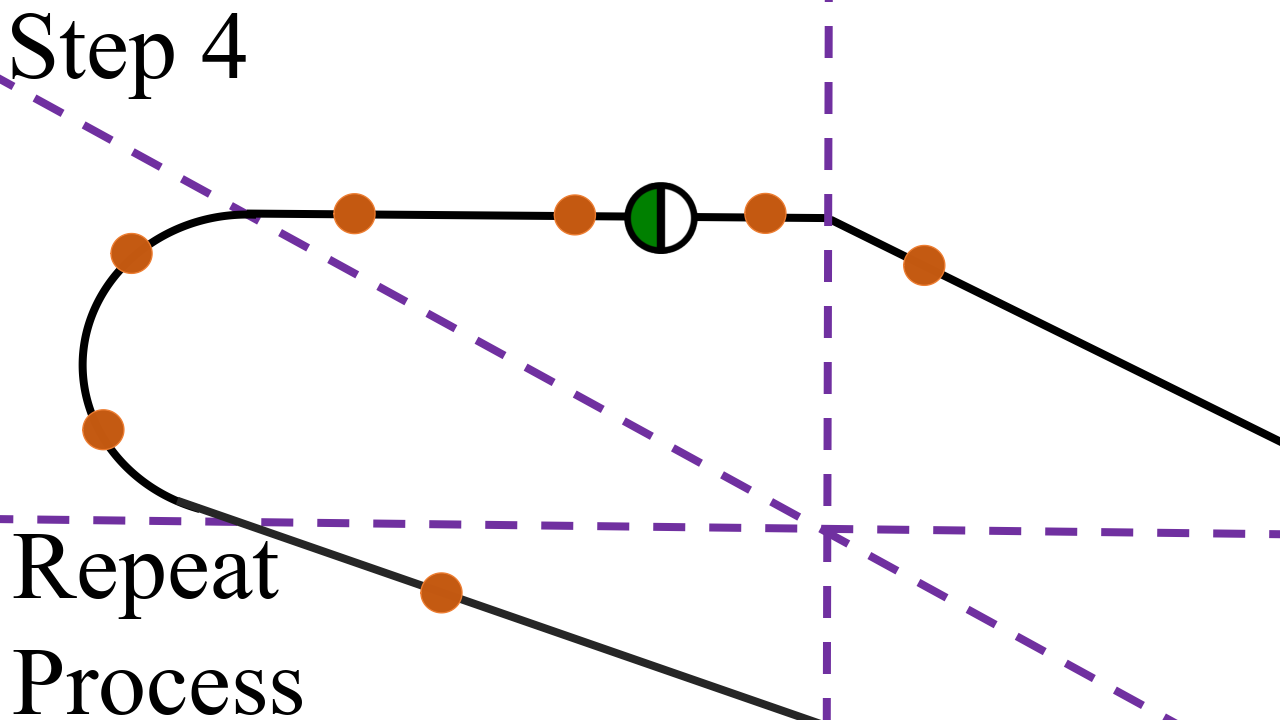
Figure 1: Illustration of the iterative procedure for computing stable manifolds with subregion boundaries indicated in purple-dashed.

These steps ensure the manifold’s path across subregions is continuous, thus effectively mapping the global structure as determined by the dynamics of the neural network. A critical innovation is the ability to track manifold foldings, which might indicate transitions and bifurcations between various states, directly affecting stability and chaos detection.

Practical Implications

Applications in Scientific and Medical Domains

The reconstruction capabilities offered by PLRNNs, especially enhanced by the stable manifold finding algorithm, serve crucial roles in domains such as neuroscience and time series prediction. The algorithm’s ability to identify and delineate basins of attraction can directly translate to understanding how neural networks, and consequently, cerebral functions, manage memory and decision-making processes:

• Decision-Making Models: With basins categorizing distinct attractor states, these methods can interpret neuronal decision processes, allowing for dynamic mapping of neural activity and facilitating accurate model predictions.
• Electrophysiological Recordings Analysis: Application of the algorithm to actual recorded data from cortical neurons provides vital insights into the cyclical and stable behaviors, crucial for understanding neurocognitive functions such as spiking and persistent activity.

Computational Considerations

Efficiency and Resource Usage

The algorithm benefits from polynomial time scaling with the dimensions of latent spaces due to the efficient handling of the linear subregions dictated by ReLU functions. Nonetheless, it may face challenges in particularly high-dimensional instances where the curse of dimensionality becomes pronounced, especially in chaotic systems with manifold foldings:

• Invertibility Requirement: The algorithm performs optimally when the mapping is invertible, a condition ensured by regularization strategies that maintain consistency across subregions.
• Algorithm Scalability: While evidence suggests tractable scalability for systems explored within the data-defined regions, the computational load may increase significantly when manifolds need to be traced in less well-defined spaces or as dimensions increase.

  Figure 2: Runtime (top-left) and reconstruction quality (bottom) as a function of latent space dimensionality $M$ for different proportions of subregions for which invertibility was enforced by regularization.

Future Developments

Extensions and Enhancements

Potential adaptations of this approach might include refining the regularization techniques to support noninvertible systems across broader parameter spaces, thus broadening applicability to more general classes of RNN architectures. Additionally, further investigations into the nature of manifold intersections and their implications for chaos theory could deepen insight into the emergent dynamics of neural networks, fostering improvements in robustness and predictive accuracy.

Conclusion

The presented algorithm marks substantial progress in the understanding and practical manipulation of RNN dynamics, particularly for systems employing piecewise-linear maps such as PLRNNs. Its efficacy in detecting stable and unstable manifolds not only aids in characterization of multistability and chaos within neural networks but also enhances model interpretability and the precision of dynamical system reconstructions across scientific domains.