Learning to Dissipate Energy in Oscillatory State-Space Models (2505.12171v1)

Abstract: State-space models (SSMs) are a class of networks for sequence learning that benefit from fixed state size and linear complexity with respect to sequence length, contrasting the quadratic scaling of typical attention mechanisms. Inspired from observations in neuroscience, Linear Oscillatory State-Space models (LinOSS) are a recently proposed class of SSMs constructed from layers of discretized forced harmonic oscillators. Although these models perform competitively, leveraging fast parallel scans over diagonal recurrent matrices and achieving state-of-the-art performance on tasks with sequence length up to 50k, LinOSS models rely on rigid energy dissipation ("forgetting") mechanisms that are inherently coupled to the timescale of state evolution. As forgetting is a crucial mechanism for long-range reasoning, we demonstrate the representational limitations of these models and introduce Damped Linear Oscillatory State-Space models (D-LinOSS), a more general class of oscillatory SSMs that learn to dissipate latent state energy on multiple timescales. We analyze the spectral distribution of the model's recurrent matrices and prove that the SSM layers exhibit stable dynamics under simple, flexible parameterizations. D-LinOSS consistently outperforms previous LinOSS methods on long-range learning tasks, without introducing additional complexity, and simultaneously reduces the hyperparameter search space by 50%.

• The paper introduces D-LinOSS, which integrates learnable damping parameters to independently control energy dissipation across different timescales.
• It employs spectral analysis and an implicit-explicit discretization method to ensure stability while mapping system parameters to eigenvalues.
• Empirical results demonstrate that D-LinOSS outperforms previous models in classification, regression, and forecasting tasks across diverse datasets.

Damped Linear Oscillatory State-Space Models

This paper introduces Damped Linear Oscillatory State-Space Models (D-LinOSS), an enhancement to Linear Oscillatory State-Space Models (LinOSS), designed to improve the representation and learning of long-range dependencies in sequential data. The key innovation is the incorporation of learnable damping parameters, which allows the model to independently control the energy dissipation of latent states at different timescales. Through spectral analysis and empirical evaluations, the authors demonstrate that D-LinOSS overcomes the limitations of previous LinOSS models, achieving state-of-the-art performance across various sequence modeling tasks.

Background and Motivation

State-space models (SSMs) have emerged as a promising architecture for sequence modeling, offering advantages over traditional RNNs and Transformers in terms of computational efficiency and the ability to capture long-range dependencies. LinOSS models, built upon layers of discretized forced harmonic oscillators, have shown competitive performance in sequence learning tasks. However, LinOSS models suffer from a limitation: their energy dissipation mechanisms are rigidly coupled to the timescale of state evolution. This restricts the model's expressive power, as it cannot independently control damping at different frequencies. D-LinOSS addresses this limitation by introducing learnable damping parameters, which enable the model to learn a wider range of stable oscillatory dynamics. (Figure 1)

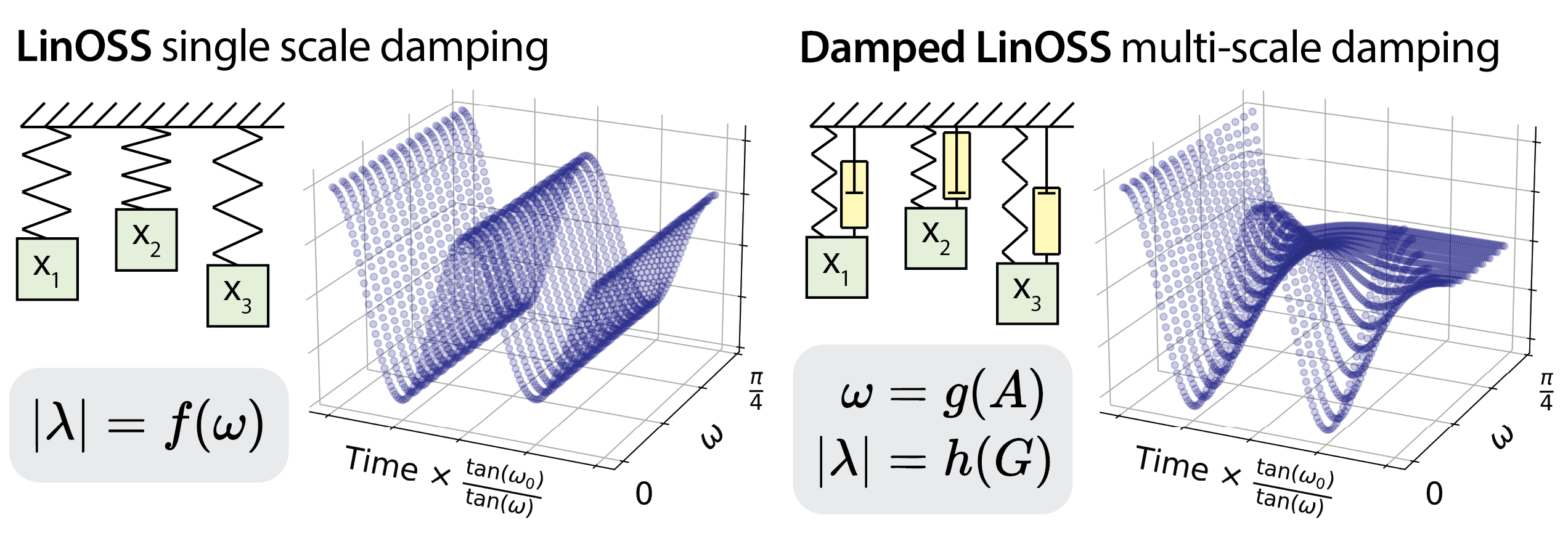
Figure 1: Previous LinOSS models couple frequency and magnitude of discretized eigenvalues, while D-LinOSS learns damping on all scales, expanding expressible internal dynamics.

Model Formulation

D-LinOSS layers are constructed from a system of damped, forced harmonic oscillators, described by a second-order ODE system:

$$\begin{aligned} x''(t) &= - A x(t) - G x'(t) + B u(t), \ y(t) &= C x(t) + D u(t) \end{aligned}$$

where $x(t)$ is the system state, $u(t)$ is the input, $y(t)$ is the output, $A$ controls the oscillation frequency, and $G$ defines the damping. Unlike previous LinOSS models where $G = 0$, D-LinOSS learns $G$, providing more flexibility in controlling energy dissipation. To solve this ODE system, it's rewritten as an equivalent first-order system and discretized using an implicit-explicit (IMEX) method to maintain stability. This discretization introduces learnable timestep parameters, $\Delta t$, which govern the integration interval. The resulting discrete-time system is described by:

$$\begin{aligned} w_{k+1} &= M w_k + F u_{k+1}, \ y_{k+1} &= H w_k \end{aligned}$$

where $M$, $F$, and $H$ are the discrete-time counterparts of the system parameters. While general SSMs require diagonalization for efficient computation, D-LinOSS benefits from block diagonal matrices, obviating the need for explicit diagonalization.

Theoretical Analysis

Spectral analysis is employed to examine the stability and dynamical behavior of D-LinOSS. The eigenvalues of the recurrent matrix $M$ govern how latent states evolve over time, with eigenvalues near unit norm retaining energy and those closer to zero dissipating energy. A key result is that D-LinOSS can represent all stable second-order systems, offering a broader range of expressible dynamics compared to previous LinOSS models.

The paper includes several propositions:

• Proposition 3.1: Provides the eigenvalues of the D-LinOSS recurrent matrix $M$ in terms of $A$, $G$, and $\Delta t$.
• Proposition 3.2: Establishes a sufficient condition for system stability, ensuring that the eigenvalues are unit-bounded when $G_i$ and $A_i$ are non-negative and $\Delta t_i \in (0, 1]$.
• Proposition 3.3: Demonstrates that the mapping from model parameters to eigenvalues is bijective, implying that D-LinOSS can represent every stable, damped, decoupled second-order system.

These theoretical results confirm that D-LinOSS overcomes the limitations of previous LinOSS models, which exhibit a rigid relationship between oscillation frequency and damping, limiting their spectral range. The authors prove that the set of stable eigenvalues reachable in D-LinOSS is the full complex unit disk, whereas the set of LinOSS eigenvalues has zero measure in $C$.

Implementation Details

To ensure stability during training, the system matrices $A$ and $G$ are parameterized using ReLU and clamping functions. This guarantees that the oscillatory dynamics remain within the stable range. Additionally, the paper introduces a procedure to initialize the recurrent matrix $M$ with eigenvalues uniformly sampled in the stable complex region. By leveraging the bijective relationship between model parameters and eigenvalues, the authors can control the spectral distribution of $M$.

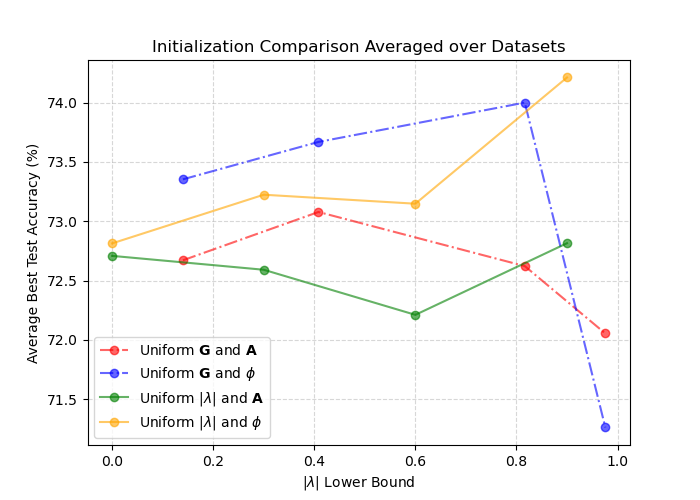
Figure 2: Initialization paper shows intervals of eigenvalue magnitude and sampling methods.

Empirical Evaluation

The empirical performance of D-LinOSS is evaluated on a range of sequence learning tasks, including time-series classification (UEA datasets), time-series regression (PPG-DaLiA), and long-horizon time-series forecasting (weather prediction). The results demonstrate that D-LinOSS consistently outperforms state-of-the-art sequence models, including Transformer-based architectures, LSTM variants, and previous versions of LinOSS. On the UEA datasets, D-LinOSS achieves the highest average test accuracy, improving upon previous state-of-the-art results. Similarly, on the PPG-DaLiA dataset, D-LinOSS reduces the mean squared error compared to existing models. For weather forecasting, D-LinOSS achieves the lowest mean absolute error, showcasing its effectiveness as a general sequence-to-sequence model.

Related Work

The paper contextualizes D-LinOSS within the broader landscape of SSMs and oscillatory neural networks. It acknowledges the foundational work on SSMs, including models based on FFT and HiPPO parameterizations. The paper also discusses the evolution of SSM architectures towards diagonal state matrices and associative parallel scans. Additionally, it highlights related models that incorporate oscillatory behavior, such as coupled oscillatory RNNs and graph-based oscillator networks.

Conclusion

D-LinOSS introduces learnable damping across all temporal scales, enabling the model to capture a wider range of stable dynamical systems. Empirical results demonstrate consistent performance gains across diverse sequence modeling tasks. The success of D-LinOSS in capturing long-range dependencies suggests that future research could explore selective variants of LinOSS, integrating the efficiency and expressiveness of LinOSS-type models with time-varying dynamics. The authors suggest that D-LinOSS will be crucial in advancing machine-learning-based approaches in domains grounded in the physical sciences because of its ability to represent temporal relationships with oscillatory structure.