Topological Invariance and Breakdown in Learning (2510.02670v1)

Abstract: We prove that for a broad class of permutation-equivariant learning rules (including SGD, Adam, and others), the training process induces a bi-Lipschitz mapping between neurons and strongly constrains the topology of the neuron distribution during training. This result reveals a qualitative difference between small and large learning rates $\eta$. With a learning rate below a topological critical point $\eta^*$, the training is constrained to preserve all topological structure of the neurons. In contrast, above $\eta^*$, the learning process allows for topological simplification, making the neuron manifold progressively coarser and thereby reducing the model's expressivity. Viewed in combination with the recent discovery of the edge of stability phenomenon, the learning dynamics of neuron networks under gradient descent can be divided into two phases: first they undergo smooth optimization under topological constraints, and then enter a second phase where they learn through drastic topological simplifications. A key feature of our theory is that it is independent of specific architectures or loss functions, enabling the universal application of topological methods to the study of deep learning.

• The paper identifies a critical learning rate (η*) below which neuron topology is preserved and above which it simplifies.
• It demonstrates that permutation-equivariant learning rules maintain topology under small learning rates and induce breakdown at larger rates.
• Empirical studies validate that adjusting learning rates can optimize network training by balancing topological preservation and simplification.

Topological Invariance and Breakdown in Learning

The paper "Topological Invariance and Breakdown in Learning" addresses the intricate dynamics of learning in neural networks, focusing on the topological transformations and constraints that emerge from different learning rules and their parameter settings. It provides a theoretical framework to understand how permutation-equivariant learning rules influence the topology of neuron distributions, revealing insights into the impact of learning rates on the training process and model expressivity.

Permutation Equivariance in Learning Rules

Permutation equivariance is a fundamental concept that supports the paper's analysis of learning dynamics. It refers to the invariance of learning algorithms with respect to permutations of neural network parameters. In neural networks, this property arises naturally in many architectures, such as fully connected layers, convolutional layers, and self-attention mechanisms, all of which exhibit permutation symmetry in the arrangement of weights and activations.

The paper establishes that permutation equivariance imposes strong topological constraints on the learning process. Specifically, under small learning rates, common learning algorithms induce bi-Lipschitz mappings between neuron distributions, thus preserving their topology (Figure 1).

Figure 1: At small learning rates, common learning algorithms induce a homeomorphic transformation of the neuron distribution, aligning with theories such as the NTK/lazy regime.

Critical Learning Rate and Topological Transitions

A key contribution of the paper is the introduction of a topological critical point, denoted $\eta^*$, below which the topology of the neuron set is preserved. When the learning rate exceeds $\eta^*$, the learning dynamics allow for topological simplifications, resulting in a coarser neuron manifold, thereby reducing model expressivity. This critical point marks the transition between two distinct phases of learning:

1. Topology-Preserving Phase: Under small learning rates, the neuron manifold's topology remains invariant. Training results in smooth optimization constrained by the preservation of topological properties.
2. Topology-Breakdown Phase: At learning rates above $\eta^*$, drastic topological changes occur, characterized by neuron merging, which reduces model complexity and expressivity.

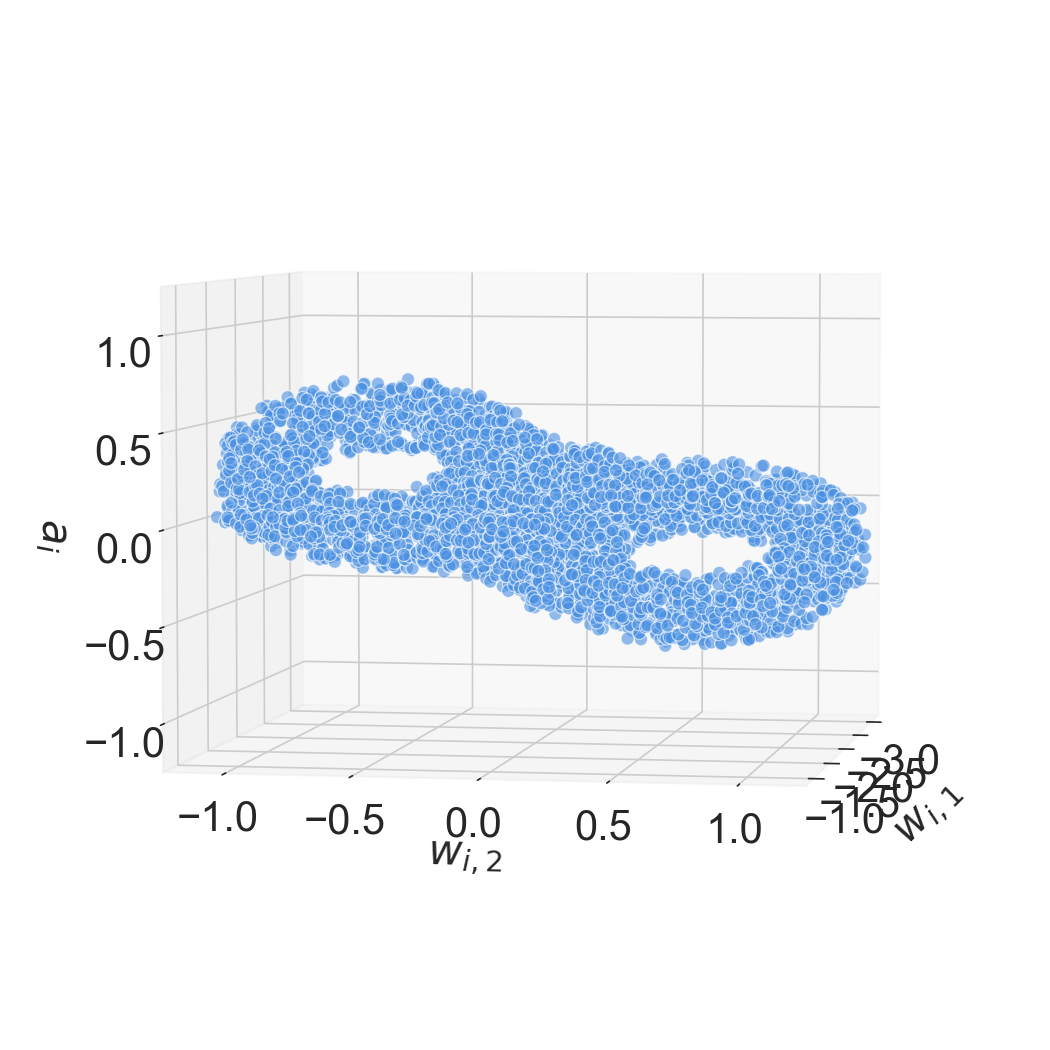
Figure 2: Topology of a 2D neural network with GD. Neurons are initialized on a genus-2 surface. Small learning rates maintain topology, while large rates alter it significantly.

Theoretical Framework and Universal Applications

The paper's theoretical framework is universal, independent of specific neural network architectures or loss functions, allowing broad application of topological methods in deep learning analysis. This universality stems from the reliance on permutation-equivariance across both architectures and optimizers like SGD and Adam. The paper precisely characterizes the learning rule's influence on topology, using concepts from mathematical topology and dynamical systems.

Figure 3: Topology of a 2D neural network with GD and disjoint genus-1 initialization; optimized with GD, reflecting topological behavior at varying learning rates.

Empirical Validation

Empirical studies support the theoretical predictions, verifying the preservation or transition of topology under different learning rates. Numerical experiments demonstrate that while neuron geometry may deform, topology remains stable with small learning rates and fragility emerges with larger ones.

Figure 4: Topology of a 3D neural network with Adam reveals topology changes with camera adjustment for visualizing the point cloud structure.

Implications and Future Research Directions

The insights from this study suggest potential improvements in training strategies, such as designing learning-rate schedules that accommodate both exploration and stability phases. Furthermore, the topological perspective opens pathways for integrating concepts from theoretical physics, particularly related to phase transitions and symmetry-breaking phenomena.

Conclusion

"Topological Invariance and Breakdown in Learning" delivers a robust framework for analyzing the complex learning dynamics in neural networks, spotlighting the pivotal role of topology and learning rates in shaping neuron distributions and model expressivity. Its universal applicability promises a foundational basis for future advancements in deep learning theory and practice.