ARMesh: Autoregressive Mesh Generation via Next-Level-of-Detail Prediction (2509.20824v1)

Abstract: Directly generating 3D meshes, the default representation for 3D shapes in the graphics industry, using auto-regressive (AR) models has become popular these days, thanks to their sharpness, compactness in the generated results, and ability to represent various types of surfaces. However, AR mesh generative models typically construct meshes face by face in lexicographic order, which does not effectively capture the underlying geometry in a manner consistent with human perception. Inspired by 2D models that progressively refine images, such as the prevailing next-scale prediction AR models, we propose generating meshes auto-regressively in a progressive coarse-to-fine manner. Specifically, we view mesh simplification algorithms, which gradually merge mesh faces to build simpler meshes, as a natural fine-to-coarse process. Therefore, we generalize meshes to simplicial complexes and develop a transformer-based AR model to approximate the reverse process of simplification in the order of level of detail, constructing meshes initially from a single point and gradually adding geometric details through local remeshing, where the topology is not predefined and is alterable. Our experiments show that this novel progressive mesh generation approach not only provides intuitive control over generation quality and time consumption by early stopping the auto-regressive process but also enables applications such as mesh refinement and editing.

• The paper introduces a transformer-based autoregressive model that progressively refines meshes starting from a single point.
• The methodology leverages a novel tokenization scheme and constrained decoding to control refinement operations and manage mesh detail levels.
• Experimental results on ShapeNet show superior coverage, matching distance, and accuracy, supporting advanced mesh editing and refinement.

ARMesh: Autoregressive Mesh Generation via Next-Level-of-Detail Prediction

This paper introduces a novel approach to generating 3D meshes using autoregressive models that are inspired by the progressive refinement techniques employed in 2D image processing. The method employs a coarse-to-fine generation strategy, leveraging simplicial complexes as a foundational representation for meshes. This strategy allows for intuitive control over detail levels during generation, facilitating applications such as mesh refinement and editing.

Transformer-Based AR Model

The primary innovation of ARMesh is the use of a transformer-based autoregressive model for progressive mesh generation. The model begins with a simplified version of a mesh, represented as a single point, and progressively refines it by adding geometric details through local remeshing. This process is akin to reversing mesh simplification, allowing for direct control over the level-of-detail (LOD) desired in the final mesh configuration.

To achieve this, the authors propose a tokenization scheme for encoding mesh refinement sequences, transforming them into a format suitable for training autoregressive models. The transformer network predicts subsequent tokens based on previously generated tokens, utilizing constrained decoding strategies to ensure valid operation sequences.

Figure 1: An example of a tokenization layout for a refinement operation.

GSlim Algorithm and Simplicial Complexes

Mesh generation in ARMesh is initialized through the GSlim algorithm, an adaptation of traditional quadric-based simplification that supports generalizations to simplicial complexes. Simplicial complexes offer a more robust framework for mesh representation, accommodating isolated points and line segments that conventional triangular meshes cannot easily describe. This allows for topological flexibility during the simplification and refinement processes.

The GSlim algorithm addresses limitations in QSlim by enabling topological changes. It assigns quadric costs to every simplex, facilitating efficient edge collapses and maintaining high geometric fidelity through weighted penalty factors.

Figure 2: Mesh simplification results at different levels of detail. Our method incorporates isolated points and edges, which also help to approximate the original fine shapes. When simplifying to 1\%, the geometric accuracy remains nearly the same.

Experimental Evaluation

Experiments conducted on datasets such as ShapeNet demonstrate the effectiveness of ARMesh in generating high-quality meshes. The results highlight significant improvements in metrics such as Coverage (COV), Minimum Matching Distance (MMD), and 1-Nearest-Neighbor Accuracy (1-NNA) over existing autoregressive models that construct meshes face-by-face.

Table \ref{tab:exp-uncond-sim-ratio} shows quantitative results comparing unconditional generation across categories, validating ARMesh's superior performance. The approach allows for flexible control over the generated mesh's complexity by prematurely terminating the autoregressive process, yielding meshes with different LODs.

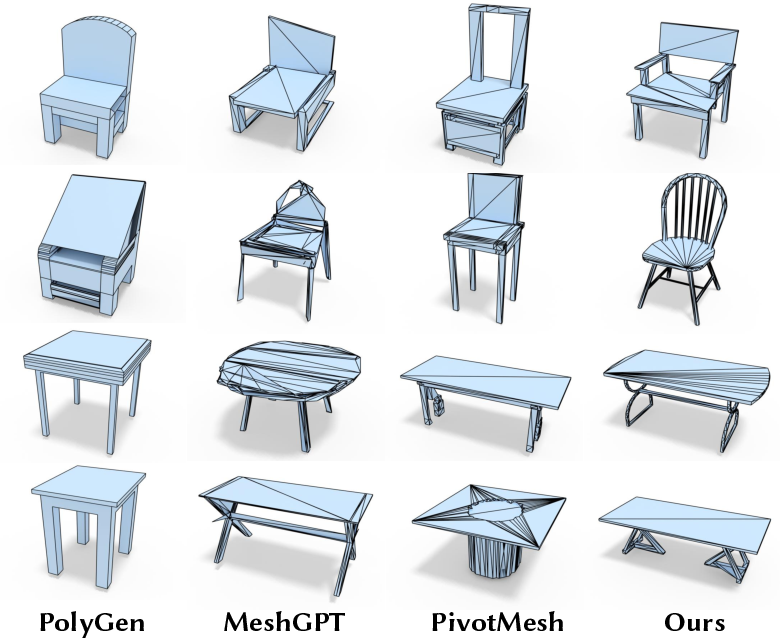
Figure 3: Visualization of unconditional direct mesh generation on the ShapeNet dataset.

Applications and Future Work

ARMesh provides practical applications in mesh editing and refinement. It enables artists to start with coarse sketches and progressively refine them into high-fidelity models. The approach also opens opportunities for continuous refinement of models by manipulating their underlying simplicial complexes.

The paper suggests future developments could include enhancing ARMesh's generalization capabilities and incorporating parallel generation techniques to improve computational efficiency. Additionally, exploring differentiable models for mesh refinement could enhance adaptability and precision in local remeshing processes.

Conclusion

ARMesh represents a significant advancement in mesh generation methodologies. By reversing the conventional simplification process, the authors establish a new paradigm for autoregressive mesh generation that intuitively matches human perceptual models of object representation. This approach not only improves generation quality but also introduces versatile applications in mesh refinement and editing, setting a precedent for future research in autoregressive 3D modeling.