floq: Training Critics via Flow-Matching for Scaling Compute in Value-Based RL (2509.06863v1)

Abstract: A haLLMark of modern large-scale machine learning techniques is the use of training objectives that provide dense supervision to intermediate computations, such as teacher forcing the next token in LLMs or denoising step-by-step in diffusion models. This enables models to learn complex functions in a generalizable manner. Motivated by this observation, we investigate the benefits of iterative computation for temporal difference (TD) methods in reinforcement learning (RL). Typically they represent value functions in a monolithic fashion, without iterative compute. We introduce floq (flow-matching Q-functions), an approach that parameterizes the Q-function using a velocity field and trains it using techniques from flow-matching, typically used in generative modeling. This velocity field underneath the flow is trained using a TD-learning objective, which bootstraps from values produced by a target velocity field, computed by running multiple steps of numerical integration. Crucially, floq allows for more fine-grained control and scaling of the Q-function capacity than monolithic architectures, by appropriately setting the number of integration steps. Across a suite of challenging offline RL benchmarks and online fine-tuning tasks, floq improves performance by nearly 1.8x. floq scales capacity far better than standard TD-learning architectures, highlighting the potential of iterative computation for value learning.

• The paper introduces floq, which reparameterizes Q-functions as flow-matched velocity fields, enabling scalable critic capacity with adjustable integration steps.
• The paper employs a TD-bootstrapped flow-matching loss with dense supervision across integration steps, ensuring robust learning compared to standard TD methods.
• Empirical results show floq outperforms state-of-the-art baselines by up to 1.8× on hard offline RL tasks and adapts well during online fine-tuning.

Flow-Matching Q-Functions: Scaling Critic Capacity in Value-Based RL

Introduction and Motivation

The paper introduces floq, a novel approach for parameterizing and training Q-functions in value-based reinforcement learning (RL) using flow-matching techniques. The central motivation is to address the limitations of monolithic Q-function architectures, which often fail to leverage increased model capacity effectively, especially in challenging offline RL settings. Drawing inspiration from the success of iterative computation and dense intermediate supervision in large-scale LLMs and diffusion models, the authors propose to represent the Q-function as a velocity field over a scalar latent, trained via a flow-matching objective. This enables fine-grained scaling of Q-function capacity by adjusting the number of integration steps, rather than simply increasing network depth or width.

Methodology: Flow-Matching Q-Functions

Parameterization

floq departs from standard Q-function parameterizations by modeling the Q-value as the result of numerically integrating a learned velocity field $v_\theta(t, z \mid s, a)$ over a scalar latent $z$, conditioned on state-action pairs. The process starts with $z \sim \mathrm{Unif}[l, u]$ and integrates the velocity field from $t=0$ to $t=1$, such that the final output $\psi_\theta(1, z \mid s, a)$ approximates the Q-value $Q^\pi(s, a)$. The number of integration steps $K$ directly controls the effective "depth" and expressivity of the critic.

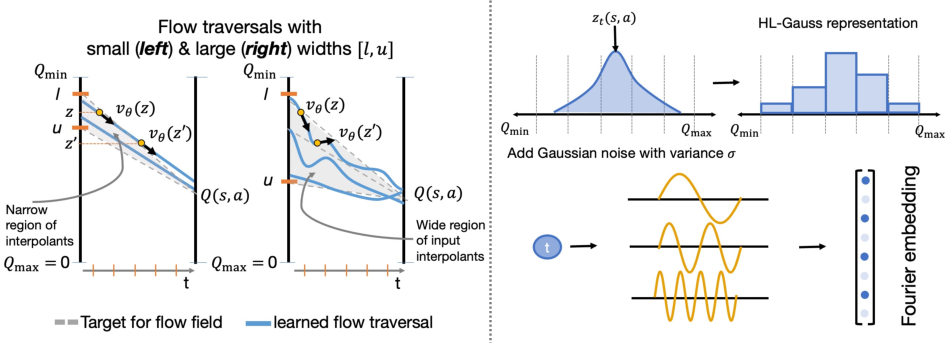
Figure 1: The effect of interval width $[l, u]$ on flow curvature and the categorical/Fourier representations for $z$ and $t$.

Training Objective

The velocity field is trained using a TD-bootstrapped flow-matching loss. For each transition $(s, a, r, s')$, a target Q-value is computed by integrating a target velocity field (a moving average of the main network) at the next state-action pair. The flow-matching loss supervises the velocity field at interpolated points $z(t) = (1-t)z + t y(s, a)$, where $y(s, a)$ is the TD target, enforcing the velocity to match the displacement from $z$ to $y(s, a)$. This provides dense supervision at all integration steps, in contrast to standard TD learning which only supervises the final output.

Practical Design Choices

The authors identify two critical design choices for stable and effective training:

1. Initial Noise Distribution: The support $[l, u]$ for $z$ must be wide and overlap with the range of Q-values encountered during training. Too narrow or misaligned intervals cause the flow to degenerate to a monolithic critic or produce unstable learning.
2. Input Representations: To address non-stationarity in $z(t)$ and $t$, the interpolant is encoded using a categorical HL-Gauss embedding, and time is embedded via a high-dimensional Fourier basis. These choices are essential for the velocity field to utilize the inputs meaningfully and avoid collapse.

Empirical Evaluation

Offline RL Performance

floq is evaluated on the OGBench suite, which comprises high-dimensional, sparse-reward, and long-horizon tasks. The method is compared against state-of-the-art offline RL algorithms, including FQL (Flow Q-Learning), ReBRAC, DSRL, and SORL. floq consistently outperforms all baselines, with the most pronounced gains on the hardest environments. Notably, floq achieves up to 1.8$\times$ the performance of FQL on hard tasks, and the improvement is robust across median, IQM, mean, and optimality gap metrics.

Figure 2: floq outperforms FQL across all aggregate metrics, with non-overlapping confidence intervals.

Online Fine-Tuning

In online fine-tuning experiments, floq provides a stronger initialization from offline RL and maintains its advantage throughout online adaptation, leading to faster convergence and higher final success rates.

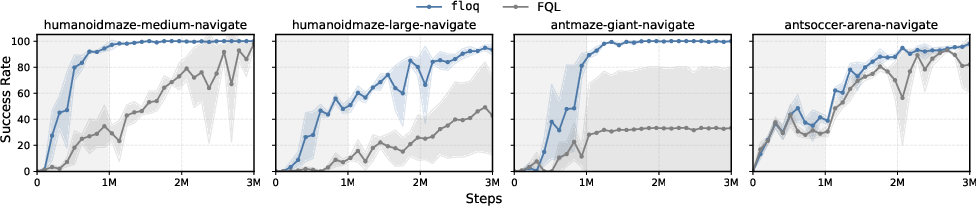
Figure 3: floq maintains a consistent advantage over FQL during online fine-tuning on hard tasks.

Scaling and Ablation Studies

• Integration Steps: Increasing the number of flow steps generally improves performance, but excessive steps can lead to diminishing or negative returns due to overfitting or numerical instability. Moderate values (e.g., $K=4$ or $8$) are optimal for most tasks.

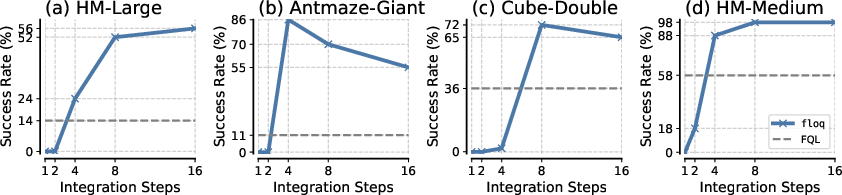
  Figure 4: More flow steps improve performance, but too many can degrade it, especially on complex tasks.

• Comparison to Ensembles and ResNets: floq outperforms monolithic ensembles and deep ResNets, even when matched for total compute. The sequential, recursively conditioned integration in floq provides expressivity not attainable by parallel ensembles or deeper residual architectures.

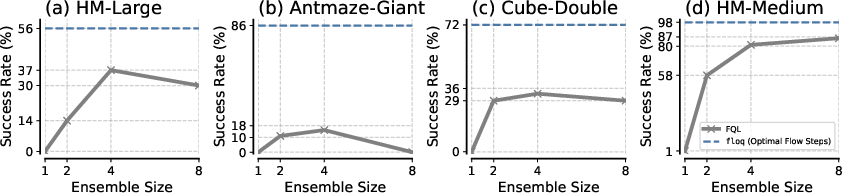
  Figure 5: floq surpasses monolithic ensembles of up to 8 critics, demonstrating superior compute scaling.

• Dense Supervision: Supervising the velocity field at all integration steps is crucial. Restricting supervision to $t=0$ yields some gains over FQL but falls short of full floq.
• Input Embeddings: HL-Gauss embeddings for $z(t)$ and Fourier embeddings for $t$ are both necessary for stable and high performance. Scalar or normalized scalar embeddings, or omitting the Fourier basis, result in significant performance drops.

  Figure 6: HL-Gauss embeddings and large $\sigma$ values for $z(t)$ are critical for robust performance.

• Noise Variance: The variance of the initial noise distribution controls the curvature of the flow. Too little curvature collapses the model to a monolithic critic; too much makes integration difficult.

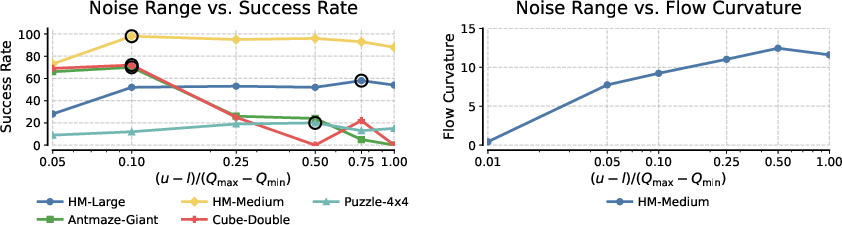
  Figure 7: Success rates and flow curvature as a function of initial noise variance, highlighting the need for moderate curvature.

• Policy Extraction Steps: The number of integration steps used for policy extraction is less critical, provided the TD target is computed with sufficient accuracy.

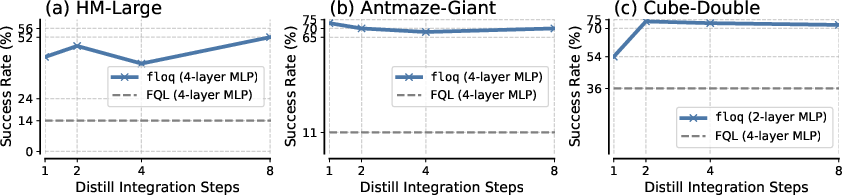
  Figure 8: Policy extraction is robust to the number of integration steps, as long as TD targets are accurate.

Theoretical and Practical Implications

floq demonstrates that iterative computation with dense intermediate supervision is a viable and effective axis for scaling Q-function capacity in value-based RL. The approach enables "test-time scaling" by increasing the number of integration steps without increasing parameter count, providing a flexible trade-off between compute and performance. The results challenge the prevailing assumption that simply increasing network depth or width is sufficient for scaling value-based RL, highlighting the importance of architectural and training objective innovations.

Theoretically, the work suggests that curved flow traversals enable the critic to perform error correction and more expressive value estimation, analogous to iterative refinement in LLMs and diffusion models. The dense auxiliary tasks provided by the flow-matching loss may also enhance representation learning, a hypothesis supported by the observed empirical gains.

Future Directions

Several open questions arise from this work:

• Optimal Integration Step Selection: Determining the optimal number of integration steps for a given task and dataset remains an open problem, as excessive steps can degrade performance.
• Test-Time Scaling and Model Selection: floq's ability to represent a family of critics with varying capacities in a single network could enable new workflows for model selection, deployment-time scaling, and efficient policy extraction.
• Combination with Parallel Scaling: Investigating how sequential scaling via floq can be combined with parallel scaling (ensembles) and other architectural innovations.
• Theoretical Analysis: Formalizing the representational and computational benefits of flow-matching critics, especially in the context of TD learning and auxiliary task design.

Conclusion

floq provides a principled and empirically validated approach for scaling Q-function capacity in value-based RL via flow-matching and iterative computation. The method achieves state-of-the-art results on challenging offline RL benchmarks, outperforms alternative scaling strategies, and introduces a new paradigm for leveraging compute in critic architectures. The work opens several avenues for further research in both the theoretical understanding and practical deployment of scalable RL systems.