Attention Mamba: Time Series Modeling with Adaptive Pooling Acceleration and Receptive Field Enhancements (2504.02013v1)

Abstract: "This work has been submitted to the lEEE for possible publication. Copyright may be transferred without noticeafter which this version may no longer be accessible." Time series modeling serves as the cornerstone of real-world applications, such as weather forecasting and transportation management. Recently, Mamba has become a promising model that combines near-linear computational complexity with high prediction accuracy in time series modeling, while facing challenges such as insufficient modeling of nonlinear dependencies in attention and restricted receptive fields caused by convolutions. To overcome these limitations, this paper introduces an innovative framework, Attention Mamba, featuring a novel Adaptive Pooling block that accelerates attention computation and incorporates global information, effectively overcoming the constraints of limited receptive fields. Furthermore, Attention Mamba integrates a bidirectional Mamba block, efficiently capturing long-short features and transforming inputs into the Value representations for attention mechanisms. Extensive experiments conducted on diverse datasets underscore the effectiveness of Attention Mamba in extracting nonlinear dependencies and enhancing receptive fields, establishing superior performance among leading counterparts. Our codes will be available on GitHub.

• The paper introduces Attention Mamba, an architecture that leverages an Adaptive Pooling block and bidirectional Mamba blocks to model nonlinear dependencies and expand receptive fields.
• The novel design accelerates computation by reducing training time by 42.6% while achieving superior forecasting accuracy as measured by MSE and MAE.
• Ablation studies confirm the critical contribution of the Adaptive Pooling block in enhancing global feature extraction for diverse time series applications.

Attention Mamba: Adaptive Pooling for Enhanced Time Series Modeling

The paper "Attention Mamba: Time Series Modeling with Adaptive Pooling Acceleration and Receptive Field Enhancements" (2504.02013) introduces a novel architecture, Attention Mamba, designed to improve time series forecasting (TSF) by addressing limitations in existing Mamba-based models, specifically insufficient modeling of nonlinear dependencies and restricted receptive fields. Attention Mamba incorporates an Adaptive Pooling block to accelerate attention computation and capture global information, along with a bidirectional Mamba block to extract both long- and short-term features.

Architecture and Implementation

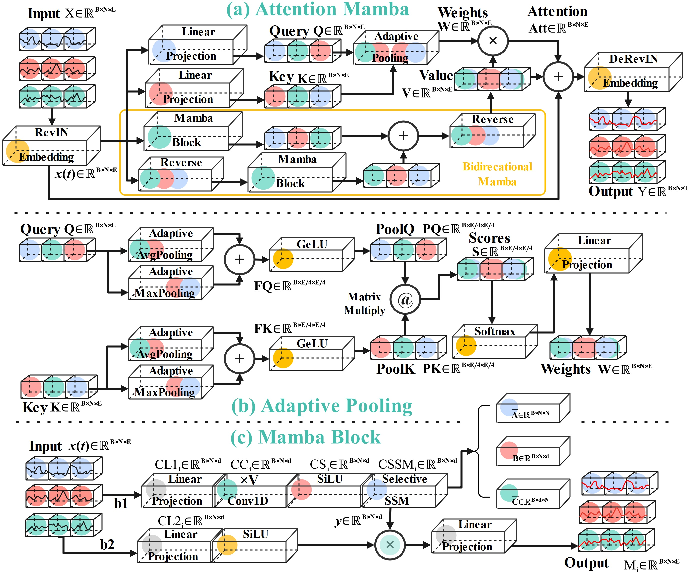
Figure 1: The overall and detailed component architectures involved in Attention Mamba; (a) the overall architecture of Attention Mamba with paired RevIN layers used to reduce non-stationary occurrence; (b) the Adaptive Pooling block that accelerates attention computation and provides wider receptive fields; (c) the framework of Mamba that composes the core of the bidirectional Mamba block.

The architecture of Attention Mamba (Figure 1a) begins with two linear projections to generate Query and Key matrices. The Adaptive Pooling block (Figure 1b) then downscales these matrices to one-quarter of their original size using adaptive average and max pooling. This reduction aims to accelerate computation while retaining global information. The fused adaptive pooling equation is defined as:

$$\begin{aligned} \mathbf{FQ} & = \operatorname{AvgPooling}(\mathbf{Q}) + \operatorname{MaxPooling}(\mathbf{Q}) \ \mathbf{FK} & =\operatorname{AvgPooling}(\mathbf{K}) + \operatorname{MaxPooling}(\mathbf{K}), \end{aligned}$$

where $\mathbf{Q}$ and $\mathbf{K}$ represent the Query and Key matrices, respectively, and $\mathbf{FQ}$ and $\mathbf{FK}$ are the resulting fused Query and Key matrices. A GeLU activation function is applied to introduce nonlinearity:

$$\begin{aligned} \mathbf{PoolQ} & = \operatorname{GeLU}(\mathbf{FQ}) \ \mathbf{PoolK} & =\operatorname{GeLU}(\mathbf{FK}) \ \mathbf{Scores} & = \mathbf{PoolQ} @\mathbf{PoolK}, \end{aligned}$$

The $\mathbf{Scores}$ matrix is then processed through a Softmax function and a linear projection to obtain the final $\mathbf{Weights}$.

Simultaneously, the input is processed by a bidirectional Mamba block (Figure 1c) to generate a refined $\mathbf{Value}$ representation. The bidirectional Mamba block is defined as:

$$\begin{aligned} &\operatorname{Normal Process:}\quad\operatorname{Mamba}(x) \ &\operatorname{Reverse Process:}\quad\operatorname{Mamba}(\operatorname{RVS}(x)) \ &\mathbf{Value}=\operatorname{RVS}(\operatorname{Normal Process} + \operatorname{Reverse Process}), \end{aligned}$$

where $\operatorname{RVS}$ denotes the reverse operation on sequences, and $\operatorname{Mamba}$ represents the selective state space modeling process. Finally, the attention mechanism is applied by weighting the $\mathbf{Value}$ with the computed $\mathbf{Weights}$:

$$\mathbf{Att}=\mathbf{Weights} \times \mathbf{Value}.$$

Experimental Results

The paper evaluates Attention Mamba on seven real-world datasets, including Electricity, Weather, Solar-Energy, and four PEMS datasets (03, 04, 07, 08). These datasets cover a range of applications such as electricity consumption forecasting, weather prediction, and traffic management. The performance of Attention Mamba is compared against ten state-of-the-art (SOTA) models, including Transformer-based models (iTransformer, PatchTST, Crossformer, FEDformer, Autoformer), Linear-based models (RLinear, TiDE, DLinear), a Temporal Convolutional Network-based model (TimesNet), and a Mamba-based model (S-Mamba). The evaluation metrics used are Mean Squared Error (MSE) and Mean Absolute Error (MAE).

The results demonstrate that Attention Mamba achieves superior performance compared to its counterparts across various datasets and forecasting windows. Specifically, Attention Mamba exhibits enhanced capabilities in extracting nonlinear dependencies and widening receptive fields.

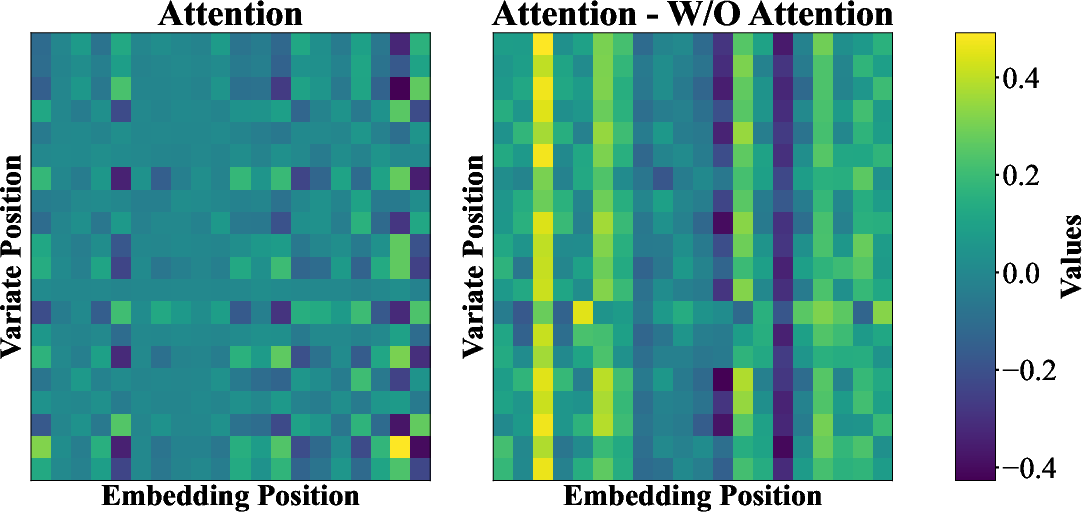
Figure 2: A snapshot of the attention map of PEMS04 with the forecasting window at 48 to visually demonstrate the enhanced receptive fields. Attention represents the input weighted by the Adaptive Pooling block, and W/O Attention represents the original input.

A visualization of the attention map in PEMS04 (Figure 2) highlights how the Adaptive Pooling block enhances receptive fields, allowing the model to focus on key features. The Friedman nonparametric test confirms that Attention Mamba ranks first in both MSE and MAE, demonstrating its overall effectiveness.

Performance Analysis and Ablation Studies

Ablation studies were conducted to assess the individual contributions of the Adaptive Pooling block and the bidirectional Mamba block. Comparisons between Attention Mamba and S-Mamba (a bidirectional Mamba model) reveal the effectiveness of the Adaptive Pooling block in enhancing nonlinear dependency extraction. The results indicate that the Adaptive Pooling block consistently improves performance, particularly in scenarios where the embedding dimension is smaller than the number of variates.

Resource Utilization

The paper also analyzes the memory and computational complexity of Attention Mamba. Compared to S-Mamba, Attention Mamba reduces training time by 42.6% but increases memory occupation by 34% due to the attention mechanism. The authors argue that the accuracy gains outweigh the increased memory costs.

Conclusion

The Attention Mamba architecture presents a promising approach to time series forecasting by integrating adaptive pooling techniques with bidirectional Mamba blocks. The Adaptive Pooling block effectively enhances receptive fields and improves the extraction of nonlinear dependencies, leading to superior forecasting performance. Future research directions include developing a dynamic input-dependent adaptive pooling scheme to address current limitations.