A Brain-Inspired Gating Mechanism Unlocks Robust Computation in Spiking Neural Networks (2509.03281v1)

Abstract: While spiking neural networks (SNNs) provide a biologically inspired and energy-efficient computational framework, their robustness and the dynamic advantages inherent to biological neurons remain significantly underutilized owing to oversimplified neuron models. In particular, conventional leaky integrate-and-fire (LIF) neurons often omit the dynamic conductance mechanisms inherent in biological neurons, thereby limiting their capacity to cope with noise and temporal variability. In this work, we revisit dynamic conductance from a functional perspective and uncover its intrinsic role as a biologically plausible gating mechanism that modulates information flow. Building on this insight, we introduce the Dynamic Gated Neuron~(DGN), a novel spiking unit in which membrane conductance evolves in response to neuronal activity, enabling selective input filtering and adaptive noise suppression. We provide a theoretical analysis showing that DGN possess enhanced stochastic stability compared to standard LIF models, with dynamic conductance intriguingly acting as a disturbance rejection mechanism. DGN-based SNNs demonstrate superior performance across extensive evaluations on anti-noise tasks and temporal-related benchmarks such as TIDIGITS and SHD, consistently exhibiting excellent robustness. Our results highlight, for the first time, a biologically plausible dynamic gating as a key mechanism for robust spike-based computation, providing not only theoretical guarantees but also strong empirical validations. This work thus paves the way for more resilient, efficient, and biologically inspired spiking neural networks.

• The paper introduces a Dynamic Gated Neuron (DGN) model that integrates biologically-inspired dynamic conductance for adaptive noise suppression in spiking neural networks.
• It demonstrates via theoretical SDE analysis and empirical benchmarks that the DGN model outperforms standard LIF neurons, achieving 99.10% top-1 accuracy on TIDIGITS.
• The study reveals a structural homology between DGN and LSTM units, suggesting a unified framework for robust temporal information processing.

Brain-Inspired Dynamic Gating for Robust Spiking Neural Computation

Introduction

This paper introduces the Dynamic Gated Neuron (DGN), a spiking neuron model that incorporates biologically inspired dynamic conductance as a gating mechanism to modulate information flow and enhance robustness in Spiking Neural Networks (SNNs). The work addresses the limitations of conventional LIF neurons, which lack adaptive conductance mechanisms and thus fail to capture the dynamic noise rejection and temporal integration properties observed in biological neurons. The DGN model is theoretically analyzed and empirically validated on multiple temporal and neuromorphic benchmarks, demonstrating superior robustness and accuracy, particularly under noise and adversarial perturbations.

Dynamic Gated Neuron Model

The DGN model extends the standard LIF framework by introducing activity-dependent modulation of membrane conductance. The membrane potential dynamics are governed by both static leak conductance and dynamic, input-driven synaptic conductance, enabling adaptive control over information retention and noise suppression. The discrete-time update equations for DGN are:

$$D_i^t = e^{-\frac{\Delta t}{\tau_s}} D_i^{t-1} + z_i^t$$

$$\rho^t = \varphi(1 - g_l \cdot \Delta t - \Delta t \sum_i^N C_i D_i^t)$$

$$V^t = \rho^t V^{t-1} + \Delta t \sum_i^N W_i D_i^t - \vartheta z^{t-1}$$

$z^t = \Theta(V^t - \vartheta)$

where $C_i$ and $W_i$ are trainable parameters, $D_i^t$ is the filtered presynaptic input, and $\rho^t$ is the adaptive decay coefficient. This dual-pathway architecture allows the neuron to selectively filter inputs and dynamically adjust its memory retention, functionally analogous to gating operations in LSTM units.

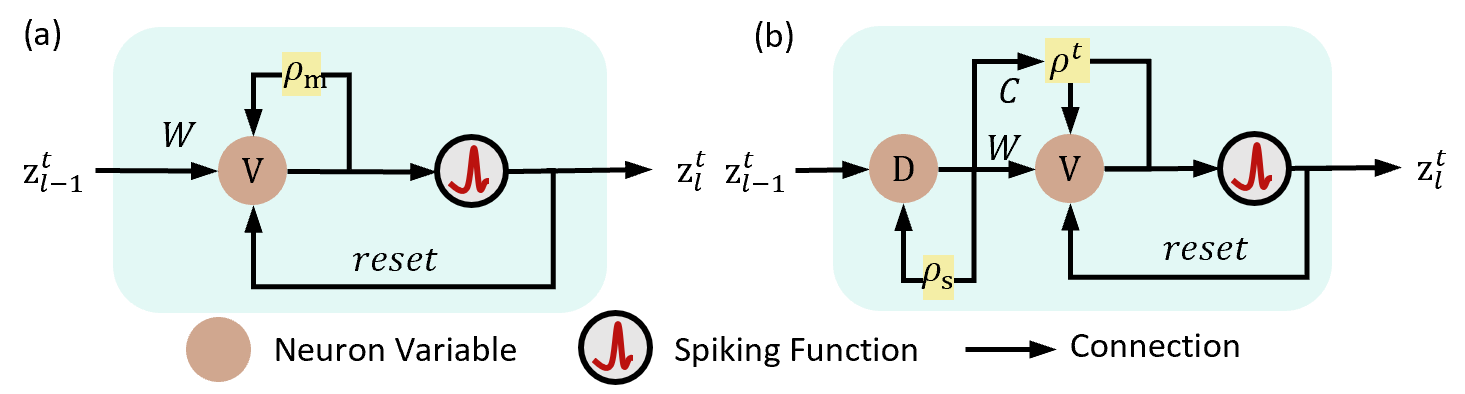
Figure 1: Schematic of the neuron models. (a) Standard LIF model. (b) DGN model with dynamic conductance gating.

Theoretical Analysis of Robustness

The paper provides a rigorous stochastic differential equation (SDE) analysis, demonstrating that DGN neurons possess enhanced stochastic stability compared to LIF neurons. The steady-state voltage variance for DGN is:

$$\langle V^2 \rangle_{\text{DGN}} = \frac{\left[\sum_{i=1}^N \sigma_i \left( W_i - \frac{C_i \sum_{j=1}^N W_j \mu_j}{G_0} \right)\right]^2}{2G_0}$$

where $G_0 = g_l + \sum C_i \mu_i$ is the effective conductance. The adaptive leakage scaling and synaptic noise compensation mechanisms in DGN enable effective voltage stabilization under stochastic input perturbations, outperforming the static noise scaling of LIF neurons.

Structural Homology with LSTM

A key insight is the topological and functional homology between DGN and LSTM architectures. The adaptive decay coefficient in DGN mirrors the forget gate in LSTM, while the dynamic integration of presynaptic currents parallels LSTM's input gating. The spike reset mechanism in DGN is mathematically congruent with LSTM's cell state update, establishing a unified framework for temporal information processing across biological and artificial systems.

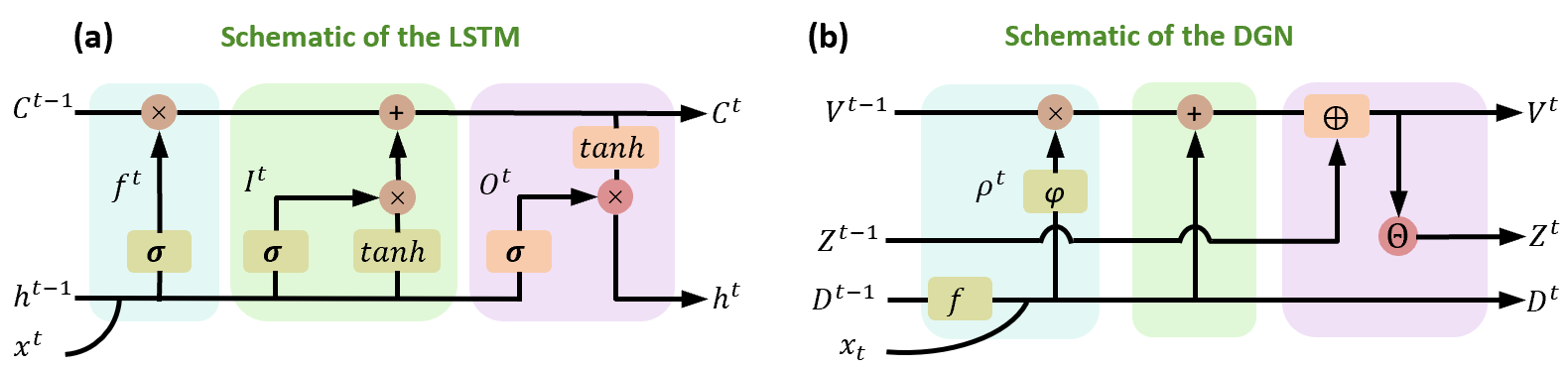
Figure 2: Schematic diagram of the model structure of LSTM and DGN, highlighting functional isomorphism in gating and memory operations.

Empirical Evaluation

State-of-the-Art Performance

DGN-based SNNs are evaluated on speech and neuromorphic datasets (Ti46Alpha, TIDIGITS, SHD, SSC) using both feedforward and recurrent architectures. The DGN model achieves:

• 99.10% top-1 accuracy on TIDIGITS (recurrent)
• 75.63% accuracy on SSC (recurrent)
• Consistently higher accuracy than LIF, ALIF, HeterLIF, and even LSTM in some configurations, despite using fewer neurons and simpler architectures.

Robustness to Noise and Adversarial Attacks

Robustness is assessed by testing models on previously unseen noise patterns and adversarial attacks (FGSM, PGD, BIM). DGN maintains high accuracy under additive, subtractive, and mixed noise, as well as gradient-based attacks, with minimal performance degradation compared to other neuron models.

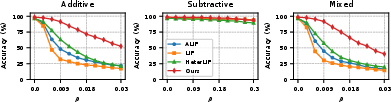
Figure 3: Performance of the model on TIDIGITS using a feedforward network under perturbations of different distribution probabilities $p$.

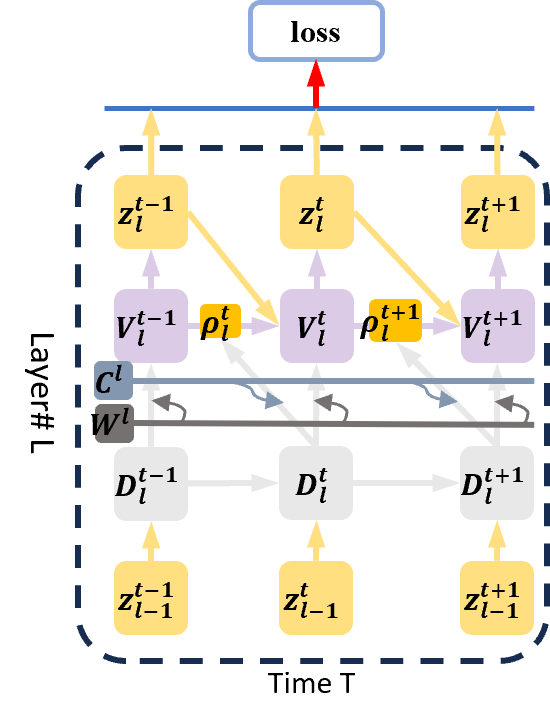
Figure 4: DGN unfolds over three time steps, illustrating temporal credit assignment for BPTT.

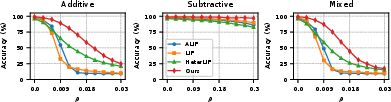
Figure 5: Performance of the model on TIDIGITS using a recurrent network under perturbations of different distribution probabilities $p$.

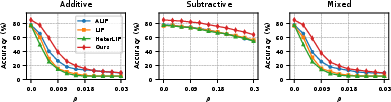
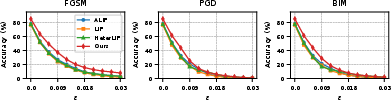
Figure 6: Performance of the model on SHD using a feedforward network under perturbations of different distribution probabilities $p$.

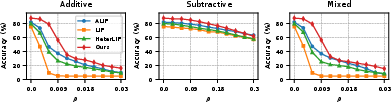
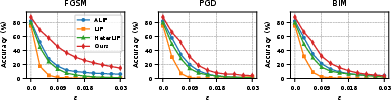
Figure 7: Performance of the model on SHD using a recurrent network under perturbations of different distribution probabilities $p$.

Ablation and Architectural Analysis

Ablation studies confirm that the dynamic gating component is essential for robust performance. Models with only static gating (leak conductance) exhibit inferior accuracy and noise resistance. The synergy between static and dynamic gating structures enables context-sensitive information filtering and adaptive noise suppression.

Implementation Considerations

• Training: DGN-SNNs are trained using BPTT with surrogate gradients, leveraging the unfolded computational graph for temporal credit assignment.
• Resource Requirements: DGN introduces minimal computational overhead compared to LIF, as the dynamic conductance update is efficiently implemented.
• Scalability: The model is compatible with standard SNN frameworks and can be deployed on neuromorphic hardware.
• Limitations: The paper focuses on robustness; further exploration of temporal dynamics and richer conductance models is warranted.

Implications and Future Directions

The DGN model bridges the gap between biophysical realism and computational efficiency in SNNs, providing a biologically plausible mechanism for robust spike-based computation. The demonstrated structural homology with LSTM units suggests a unifying principle for gating in neural computation. Future research may explore hierarchical conductance-based gating, integration with advanced SNN training methods, and deployment in real-world neuromorphic systems.

Conclusion

The Dynamic Gated Neuron model introduces a biologically inspired, activity-dependent conductance mechanism that functions as an intrinsic gating structure in spiking neural networks. Theoretical and empirical analyses demonstrate that DGN enables robust, efficient, and adaptive computation, outperforming conventional neuron models under noise and adversarial perturbations. This work establishes dynamic conductance gating as a key principle for resilient spike-based computation and opens new avenues for biologically grounded SNN design.