Ab-initio Quantum Transport with the GW Approximation, 42,240 Atoms, and Sustained Exascale Performance (2508.19138v1)

Abstract: Designing nanoscale electronic devices such as the currently manufactured nanoribbon field-effect transistors (NRFETs) requires advanced modeling tools capturing all relevant quantum mechanical effects. State-of-the-art approaches combine the non-equilibrium Green's function (NEGF) formalism and density functional theory (DFT). However, as device dimensions do not exceed a few nanometers anymore, electrons are confined in ultra-small volumes, giving rise to strong electron-electron interactions. To account for these critical effects, DFT+NEGF solvers should be extended with the GW approximation, which massively increases their computational intensity. Here, we present the first implementation of the NEGF+GW scheme capable of handling NRFET geometries with dimensions comparable to experiments. This package, called QuaTrEx, makes use of a novel spatial domain decomposition scheme, can treat devices made of up to 84,480 atoms, scales very well on the Alps and Frontier supercomputers (>80% weak scaling efficiency), and sustains an exascale FP64 performance on 42,240 atoms (1.15 Eflop/s).

• The paper presents QuaTrEx, a solver combining NEGF and self-consistent GW to simulate nanoelectronic devices with up to 84,480 atoms at exascale.
• It introduces algorithmic innovations, including domain decomposition and dynamic memoization, to achieve significant performance scaling and reduced computational overhead.
• The implementation, optimized for heterogeneous architectures, demonstrates 85% of Rmax and 56% of Rpeak on Frontier GPUs, setting a new benchmark in simulation efficiency.

Ab-initio Quantum Transport with the GW Approximation at Exascale: Methodology, Implementation, and Implications

Introduction

This work presents QuaTrEx, a quantum transport solver that integrates the non-equilibrium Green's function (NEGF) formalism with the self-consistent GW (scGW) approximation, enabling ab-initio simulations of nanoelectronic devices with up to 84,480 atoms and sustained exascale performance. The approach addresses the critical need for accurate modeling of electron-electron interactions in ultra-scaled transistors, where quantum confinement and many-body effects dominate device behavior. The implementation leverages algorithmic innovations, advanced domain decomposition, and hardware-aware programming to achieve unprecedented scale and efficiency.

Physical and Computational Background

Quantum Transport and the GW Approximation

DFT-based NEGF methods have been the standard for simulating quantum transport in nanoscale devices, but DFT's ground-state nature leads to significant inaccuracies in excited-state properties, such as underestimated band gaps and missing many-body effects. The GW approximation, based on Hedin's equations, introduces a self-energy $\Sigma = GW$ that corrects DFT results by accounting for dynamic electron-electron interactions, yielding improved agreement with experimental band structures and optical spectra.

However, the computational cost of GW, especially in its self-consistent form (scGW), is prohibitive: the standard $G_0W_0$ approach scales as $\mathcal{O}(N_A^4)$ in computation and $\mathcal{O}(N_A^3)$ in memory, where $N_A$ is the number of atoms. Extending GW to non-equilibrium (NEGF+scGW) further increases complexity, as it requires solving coupled equations for the Green's function $G$ and the screened Coulomb interaction $W$ across a dense energy grid and iterating to self-consistency.

Device and Matrix Structure

The target application is the simulation of nanoribbon field-effect transistors (NRFETs) with realistic geometries, as fabricated in advanced semiconductor technology nodes.

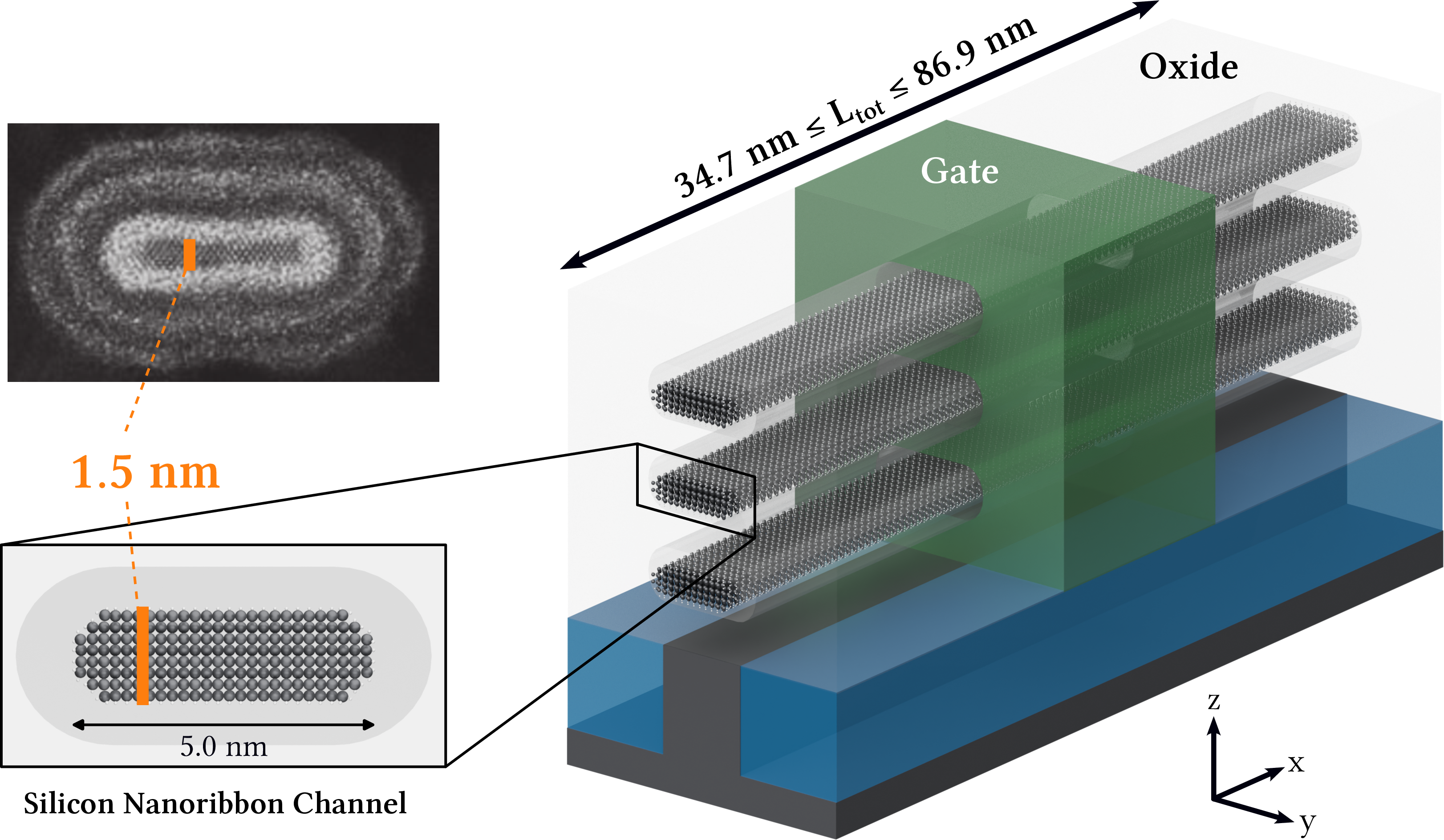
Figure 1: Schematic of a silicon nanoribbon FET with three stacked nanoribbons; the central ribbon is simulated, matching the cross-section of recent Intel devices.

The Hamiltonian and interaction matrices are constructed in a maximally localized Wannier function (MLWF) basis, yielding block-banded (BB) or block-tridiagonal (BT) sparsity patterns. This structure is exploited for both computational efficiency and memory reduction.

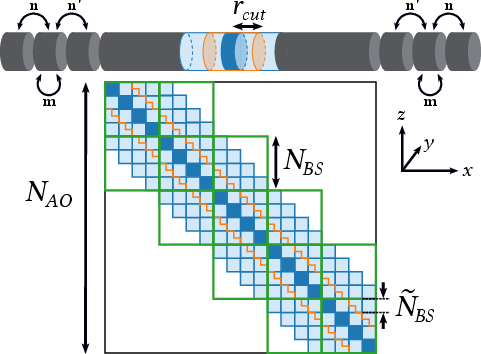
Figure 2: Mapping of a nanowire structure onto a block-banded matrix, with block-tridiagonal tiling and cutoff-induced sparsity.

Algorithmic and Software Innovations

Self-Consistent Born Approximation (SCBA) and Data Flow

The NEGF+scGW method involves iteratively solving for $G$, $W$, and their associated self-energies ($\Sigma$, $P$) across a large energy grid, with each SCBA iteration updating the data distribution and requiring efficient parallelization.

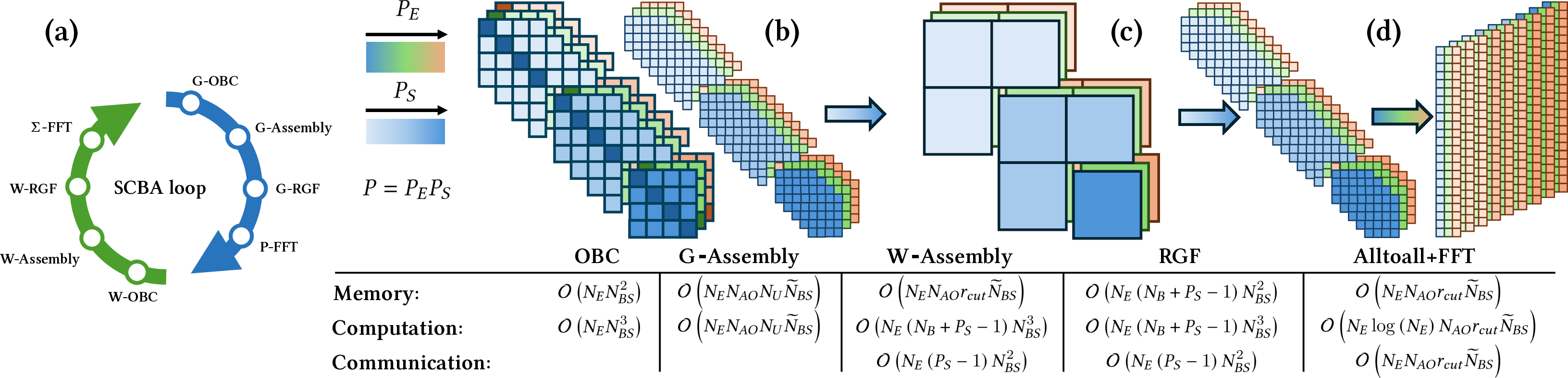
Figure 3: Data flow and distribution in an SCBA iteration, illustrating the $G \rightarrow P \rightarrow W \rightarrow \Sigma$ cycle and parallelization across energies and matrix elements.

Open Boundary Conditions (OBCs)

Accurate modeling of contacts is achieved via OBCs, computed using a combination of direct (eigenvalue-based) and iterative (fixed-point) solvers. A dynamic memoization scheme is introduced: after initial stabilization, OBCs are updated iteratively using cached results, significantly reducing computational overhead while maintaining accuracy.

Recursive Green's Function (RGF) and Distributed Solvers

The RGF algorithm is employed for efficient solution of the block-tridiagonal systems arising in NEGF+scGW, providing selected entries of the Green's function with $\mathcal{O}(N_B N_{BS}^3)$ complexity, where $N_B$ is the number of blocks and $N_{BS}$ the block size.

Figure 4: RGF's recursive Schur complement approach for computing main diagonal blocks of the selected inverse.

To overcome the inherent sequentiality of RGF and enable spatial domain decomposition, a nested-dissection scheme is implemented. This partitions the device into independent domains, allowing concurrent RGF passes and scalable distributed-memory execution.

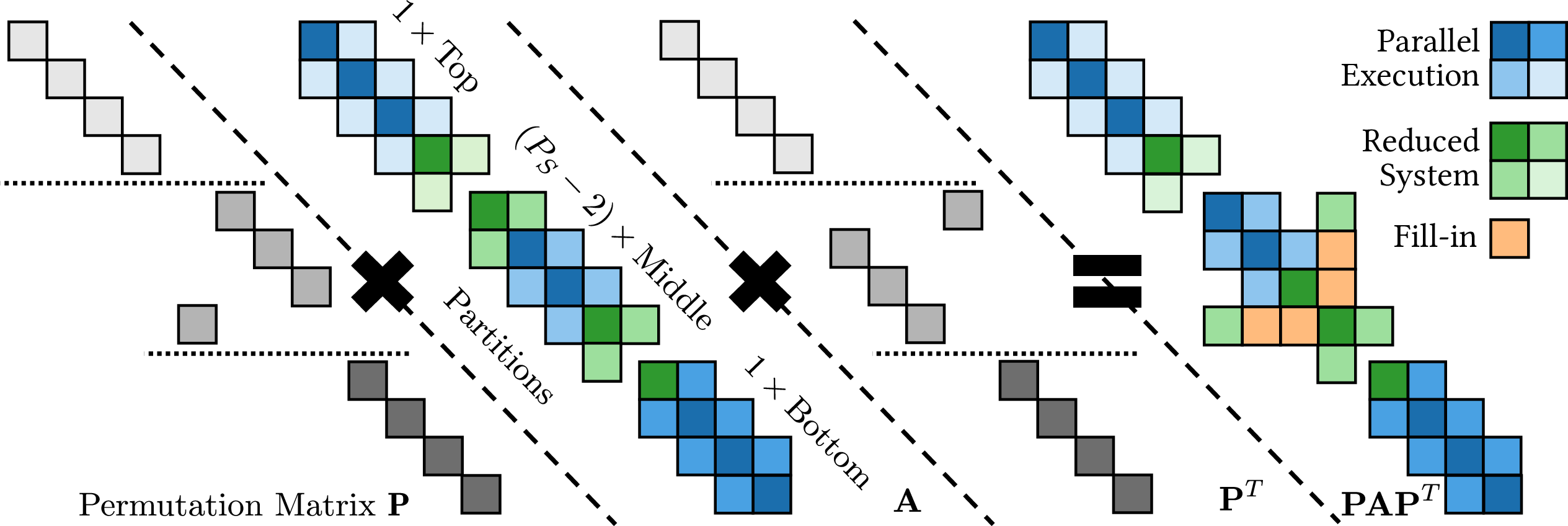
Figure 5: Nested-dissection scheme for RGF, showing permutation and partitioning of the block-tridiagonal matrix to enable parallel solution.

Symmetry Exploitation and Memory Optimization

The physical symmetries of the lesser/greater Green's functions and self-energies are enforced on-the-fly within the data structures and computational kernels, halving memory and communication requirements without sacrificing convergence stability.

Programming Model

QuaTrEx is implemented in Python, orchestrating high-performance kernels via NumPy, CuPy, mpi4py, Numba, and SciPy. Custom CPU/GPU kernels and hardware-agnostic abstractions ensure portability and performance across heterogeneous architectures (NVIDIA GH200, AMD MI250X).

Performance Evaluation

Micro-benchmarks and Scaling

QuaTrEx achieves significant speedups over its predecessor (QuaTrEx$_{24}$), with up to $3.77\times$ per-energy acceleration due to symmetry exploitation and OBC memoization. For the largest devices (NR-40, 42,240 atoms), the code sustains 1.15 Eflop/s FP64 on 37,600 GPUs (Frontier), corresponding to 85% of Rmax and 56% of Rpeak.

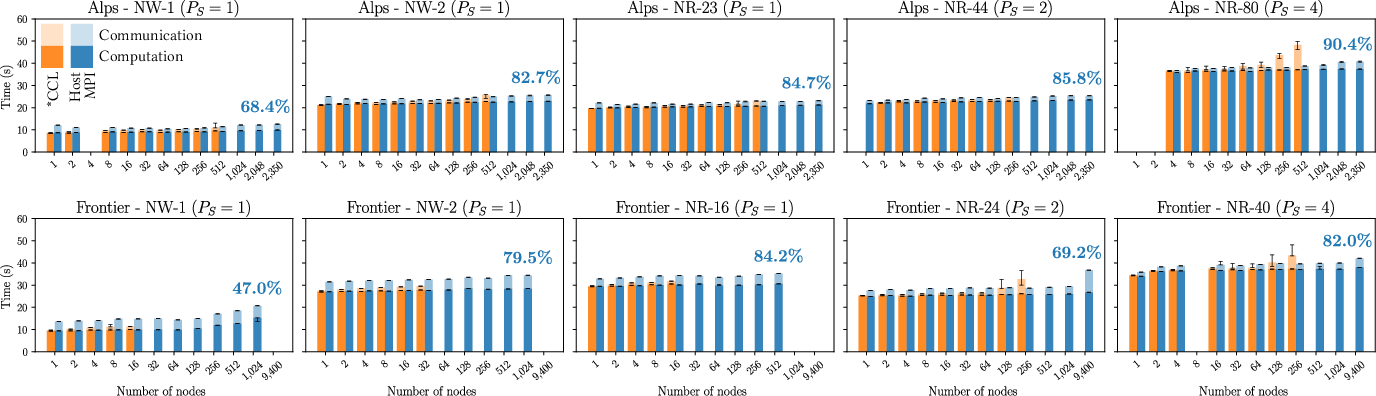
Figure 6: Weak scaling of runtime as a function of energy points, showing high parallel efficiency and breakdown of computation vs. communication.

Strong numerical results include:

• Simulation of up to 84,480 atoms and 18,800 energy points in a single run.
• SCBA iteration times of $\sim$42 seconds for 42,240 atoms, with only a 35% increase in walltime for a $16\times$ increase in workload over the previous state of the art.
• Weak scaling efficiency exceeding 80% at full system scale.

Resource Requirements and Limitations

The largest simulations are memory-bound, with the number of energy points per GPU limited by device memory. While the current implementation keeps all data on GPU to maximize compute throughput, further improvements are possible by leveraging host memory and data compression.

Practical and Theoretical Implications

QuaTrEx enables, for the first time, ab-initio quantum transport simulations of nanoelectronic devices at experimentally relevant scales, including full many-body electron-electron interactions via the GW approximation. This capability is essential for predictive modeling of next-generation transistors, where many-body effects and non-equilibrium phenomena critically determine device performance.

The modularity of the implementation allows for straightforward extension to include additional scattering mechanisms (e.g., electron-phonon, electron-photon), making QuaTrEx a reference platform for technology computer-aided design (TCAD) at the atomic scale.

The demonstrated exascale performance and scalability validate the approach for current and future heterogeneous supercomputing architectures. The innovations in domain decomposition, symmetry exploitation, and dynamic memoization are broadly applicable to other large-scale quantum many-body and transport problems.

Future Directions

Key areas for further development include:

• Increasing the number of energy points per simulation by improved memory management and data compression.
• Integration of additional physical effects (phonon, photon scattering) for comprehensive device modeling.
• Enhanced load balancing and fault tolerance for extreme-scale runs.
• Exploration of mixed-precision and reduced-order modeling to further accelerate simulations.

Conclusion

QuaTrEx establishes a new standard for ab-initio quantum transport simulations, combining the NEGF formalism with the GW approximation at unprecedented scale and efficiency. The methodological and software advances reported here enable predictive, atomistic modeling of ultra-scaled electronic devices, providing critical insights for the design and optimization of future semiconductor technologies. The approach is extensible, robust, and ready for deployment on current and next-generation exascale platforms.