SSSP-Del: Fully Dynamic Distributed Algorithm for Single-Source Shortest Path (2508.14319v1)

Abstract: Modern graphs are both large and dynamic, presenting significant challenges for fundamental queries, such as the Single-Source Shortest Path (SSSP) problem. Naively recomputing the SSSP tree after each topology change is prohibitively expensive, causing on-demand computation to suffer from high latency. Existing dynamic SSSP algorithms often cannot simultaneously handle both edge additions and deletions, operate in distributed memory, and provide low-latency query results. To address these challenges, this paper presents SSSP-Del, a new vertex-centric, asynchronous, and fully distributed algorithm for dynamic SSSP. Operating in a shared-nothing architecture, our algorithm processes streams of both edge insertions and deletions. We conduct a comprehensive evaluation on large real-world and synthetic graphs with millions of vertices, and provide a thorough analysis by evaluating result latency, solution stability, and throughput.

• The paper introduces a vertex-centric, asynchronous algorithm for dynamically updating SSSP with efficient handling of both edge additions and deletions.
• It leverages a shared-nothing architecture to minimize centralized coordination, ensuring low query latency under high update frequencies.
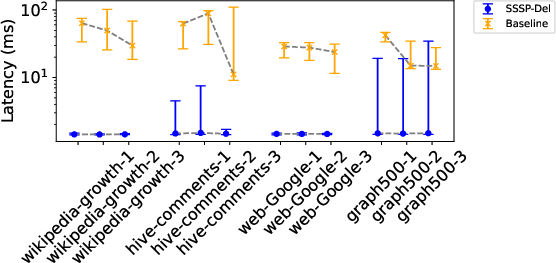
• Results demonstrate superior scalability and stability compared to traditional methods, validating its robust performance on real-world graphs.

Overview of "SSSP-Del: Fully Dynamic Distributed Algorithm for Single-Source Shortest Path"

"SSSP-Del: Fully Dynamic Distributed Algorithm for Single-Source Shortest Path" introduces a vertex-centric, asynchronous, and fully distributed algorithm designed to address the Single-Source Shortest Path (SSSP) problem in dynamic graphs. The research primarily focuses on efficiently managing both edge additions and deletions within a distributed, shared-nothing architecture. The paper emphasizes the challenges associated with maintaining low-latency query answers while processing dynamic updates, providing a comprehensive evaluation of scalability and responsiveness on real-world and synthetic graphs.

Computational Framework

The algorithm leverages a vertex-centric, asynchronous, shared-nothing computational model to perform updates efficiently in distributed environments. Each vertex manages a local state and independently processes incoming topology changes and distance updates. The architecture supports on-demand querying and minimizes centralized coordination, thus enabling scalability.

Graph Representation and Execution

Vertices are represented with unique identifiers, maintaining state related to their neighborhood connections. The execution model ensures that each vertex handles input events, updates local states, and communicates changes asynchronously across the distributed network, following a first-in, first-out message ordering to guarantee consistency.

Topological Events Handling

Updates are ingested as streams of edge additions or deletions:

• Edge Additions: Propagate distance updates through the graph using principles derived from incremental-only algorithms.
• Edge Deletions: Involve a two-phase approach: invalidation and recomputation. Affected vertices are reset, and new shortest paths are recalculated by querying neighborhoods for alternative paths.

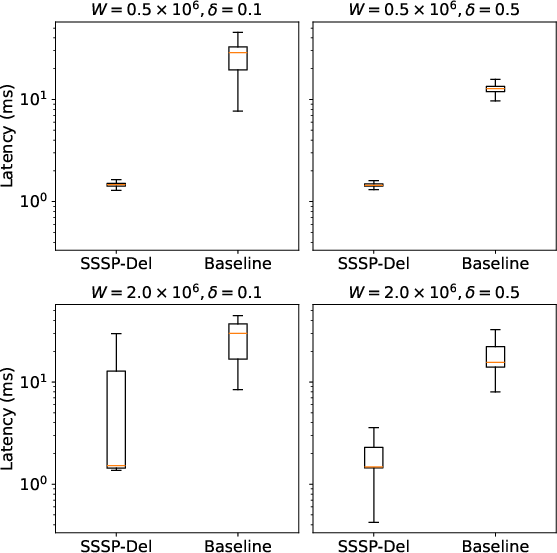
  Figure 1: Comparison of query latency between SSSP-Del and the baseline, using the web-Google dataset under four different configurations: $W=\{0.5M, 2M\} \times \delta=\{0.1, 0.5\}$.

Algorithmic Details

Vertex Properties and Message Types

Vertices store essential properties, such as distance from the source, predecessor information, and successor sets. Communication occurs through different message types to update distances, propagate invalidations, and maintain tree structure consistency even in the presence of deletions.

Phased Approach to Deletions

Upon detecting an edge deletion, vertices undergo two sequential phases:

1. Invalidation: Identifies and marks vertices affected by the deletion to invalidate their current shortest paths.
2. Recomputation: Queries incoming edges to redefine shortest paths, ensuring minimal structural changes.

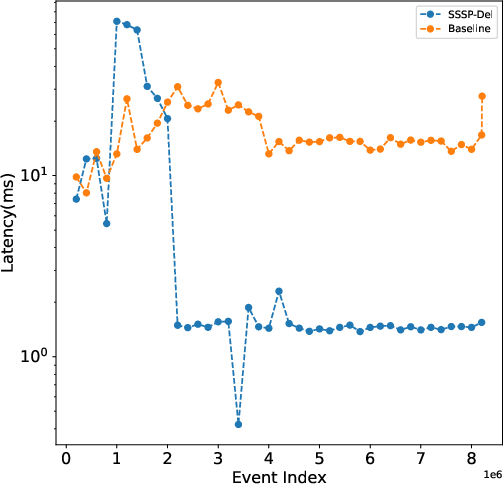
   Figure 2: Comparison of query latency between SSSP-Del and the baseline, using the web-Google dataset with W=2M and delta=0.5. The vertical axis represents the query latency in milliseconds and is in log scale, and the horizontal axis is the event index after which the query is requested.

Evaluation and Results

The evaluation showcases the algorithm's effectiveness through various performance metrics:

• Query Latency: Demonstrates substantially lower latency compared to traditional synchronous and batch-processing alternatives, especially under high update frequencies.
• Stability: Maintains consistent shortest-path results even with significant graph evolution. The algorithm exhibits high stability in response to dynamic changes, preserving structural similarities over successive queries.
• Throughput: Achieves high ingestion rates, surpassing real-world event rates, demonstrating robustness even under varying delete probabilities.

  Figure 3: Latency comparison (in milliseconds, log scale) between SSSP-Del (blue) and Baseline (orange) across multiple datasets and source selections. Each x-axis label indicates a dataset and a specific source vertex.

Comparison with Existing Frameworks

The paper compares the proposed algorithm with existing frameworks such as GraphBolt and ReMo SSSP. The results highlight the advantages of SSSP-Del in handling fine-grained dynamic updates with lower query latency, bolstered by its asynchronous processing model that efficiently interleaves algorithmic and topological event handling.

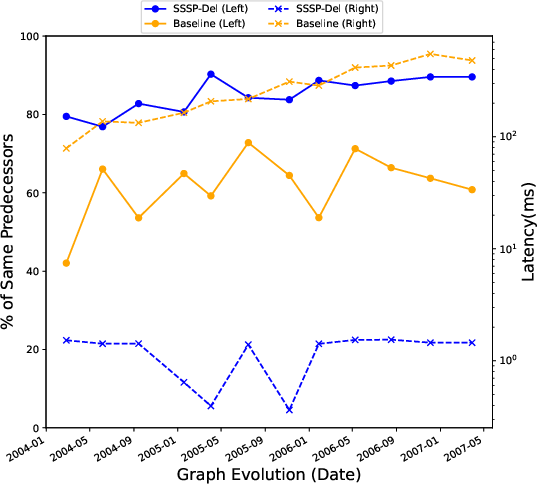
Figure 4: Stability and Result Latency over time. The graph evolution (x-axis) is plotted against the percentage of vertices in the current result that had the same predecessor in the previous result (y-axis, left) and query latency (y-axis, right). Graph: Wikipedia-growth.

Conclusion

SSSP-Del effectively addresses the dynamic SSSP problem in large, evolving graphs, providing a scalable, distributed solution capable of handling high-frequency updates with low latency. Its design principles can be extended to broader applications in dynamic graph analytics, emphasizing the balance between algorithmic efficiency and adaptability to rapidly changing data landscapes. The research sets a foundation for future developments in dynamic graph processing, especially in distributed environments, where real-time processing and stability are critical.