Sinusoidal Approximation Theorem for Kolmogorov-Arnold Networks (2508.00247v1)

Abstract: The Kolmogorov-Arnold representation theorem states that any continuous multivariable function can be exactly represented as a finite superposition of continuous single variable functions. Subsequent simplifications of this representation involve expressing these functions as parameterized sums of a smaller number of unique monotonic functions. These developments led to the proof of the universal approximation capabilities of multilayer perceptron networks with sigmoidal activations, forming the alternative theoretical direction of most modern neural networks. Kolmogorov-Arnold Networks (KANs) have been recently proposed as an alternative to multilayer perceptrons. KANs feature learnable nonlinear activations applied directly to input values, modeled as weighted sums of basis spline functions. This approach replaces the linear transformations and sigmoidal post-activations used in traditional perceptrons. Subsequent works have explored alternatives to spline-based activations. In this work, we propose a novel KAN variant by replacing both the inner and outer functions in the Kolmogorov-Arnold representation with weighted sinusoidal functions of learnable frequencies. Inspired by simplifications introduced by Lorentz and Sprecher, we fix the phases of the sinusoidal activations to linearly spaced constant values and provide a proof of its theoretical validity. We also conduct numerical experiments to evaluate its performance on a range of multivariable functions, comparing it with fixed-frequency Fourier transform methods and multilayer perceptrons (MLPs). We show that it outperforms the fixed-frequency Fourier transform and achieves comparable performance to MLPs.

• The paper presents a proof showing that learnable sinusoidal activations can achieve universal function approximation in KANs effectively.
• The methodology uses fixed-phase sinusoidal functions and Taylor series approximations to simplify complex multivariate function modeling.
• Numerical results indicate that SineKAN outperforms traditional MLPs and Fourier methods in handling rapid oscillations and singularities.

Sinusoidal Approximation Theorem for Kolmogorov-Arnold Networks

Introduction

The paper presents a novel approach to improving function approximation within Kolmogorov-Arnold Networks (KAN), by leveraging sinusoidal functions with learnable frequencies. This strategy seeks to address limitations observed in traditional neural networks, such as those employing sigmoidal activations, and positions KANs as a competitive alternative by utilizing sinusoidal approximations inspired by earlier work from Lorentz and Sprecher.

Kolmogorov-Arnold Representation

The essence of the Kolmogorov-Arnold Representation Theorem (KART) lies in its ability to represent any continuous multivariable function as a superposition of simpler, continuous single-variable functions. However, the complexity of the functions in KART's original proofs posed practical challenges. The current work simplifies this through the use of fixed-phase sinusoidal functions, aligned in a linear sequence, demonstrating that these activations can effectively capture intricate function behavior without the computational expense seen in spline-based or fixed-frequency Fourier methods.

Sinusoidal Universal Approximation Theorem

The core contribution involves the detailed proof of a theorem showcasing the universal approximation capabilities of sinusoidal activations. This work articulates that these activations, when structured appropriately, can approximate any continuous function on compact domains. The theorem encompasses the use of Taylor series for sine functions and Weierstrass approximation, underpinning the sinusoidal formulation's applicability and rigor.

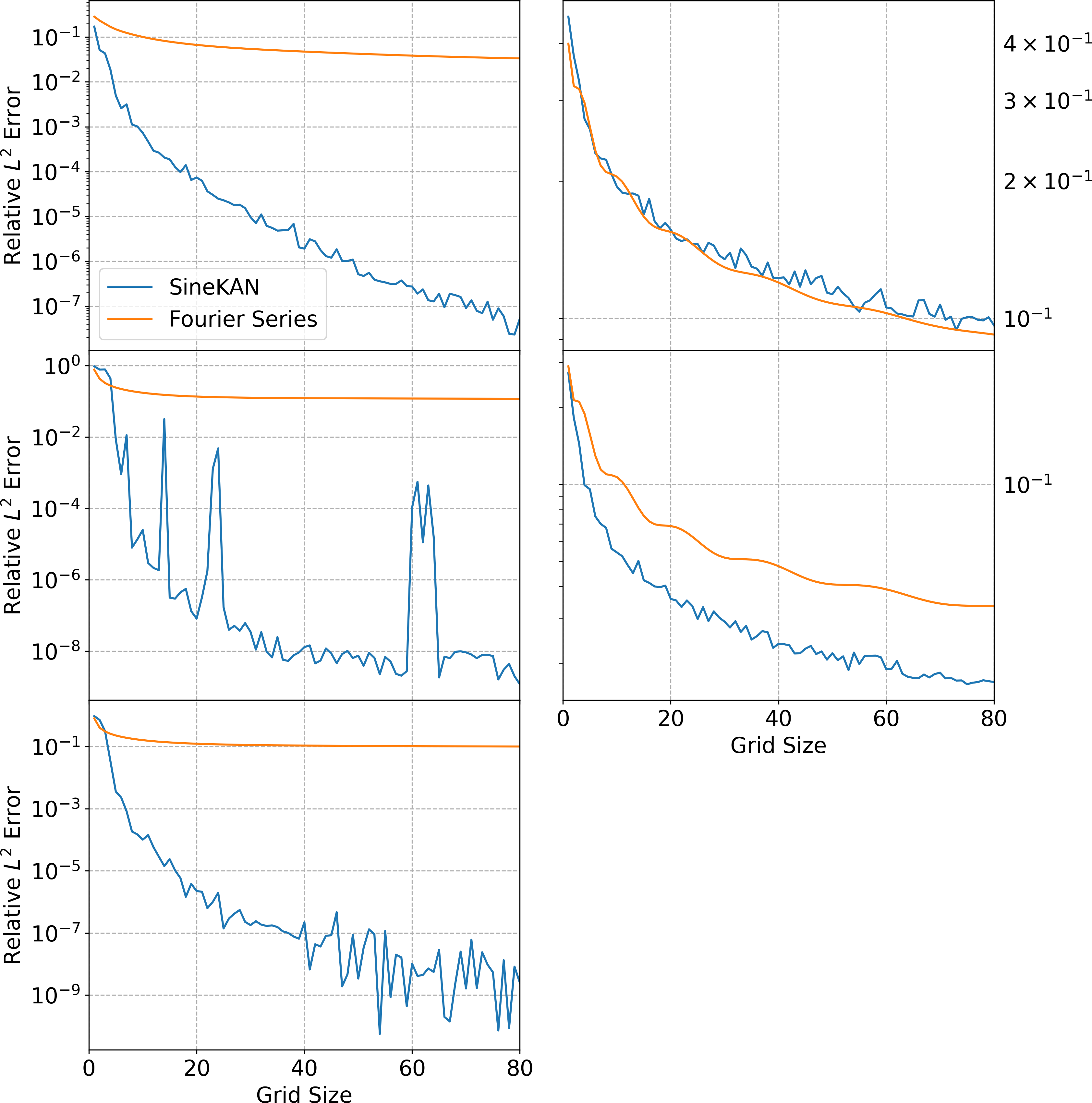
Figure 1: Approximation error as a function of grid size.

Implementation Framework

The KAN framework was adapted to utilize sinusoidal activation functions with parameters that can be tuned during training. This involves learnable frequency terms in both the inner and outer layers of the KAN, allowing for flexible function representation. Numerical experiments suggest that this model performs comparably to Multilayer Perceptrons (MLPs), specifically in handling multivariable functions with complex features.

The implementation of the SineKAN model is guided by the following neural network architecture for one-dimensional and multidimensional functions:

import numpy as np class SineKAN: def __init__(self, num_params, num_layers): self.params = np.random.rand(num_params) self.layers = num_layers def forward(self, x): y = x for _ in range(self.layers): y = np.sin(self.params[0] * y + self.params[1]) return y model = SineKAN(num_params=10, num_layers=2) output = model.forward(np.array([0.1, 0.2, 0.3])) print(output)

Numerical Analysis

Comprehensive numerical analysis demonstrates the superiority of this sinusoidal approximation approach over traditional methods, such as the Fourier series, especially when applied to functions with rapid oscillations or singularities. The paper illustrates through detailed benchmarking how the sinusoidal activations lead to lower approximation errors, outperforming even sophisticated neural network architectures in specific contexts.

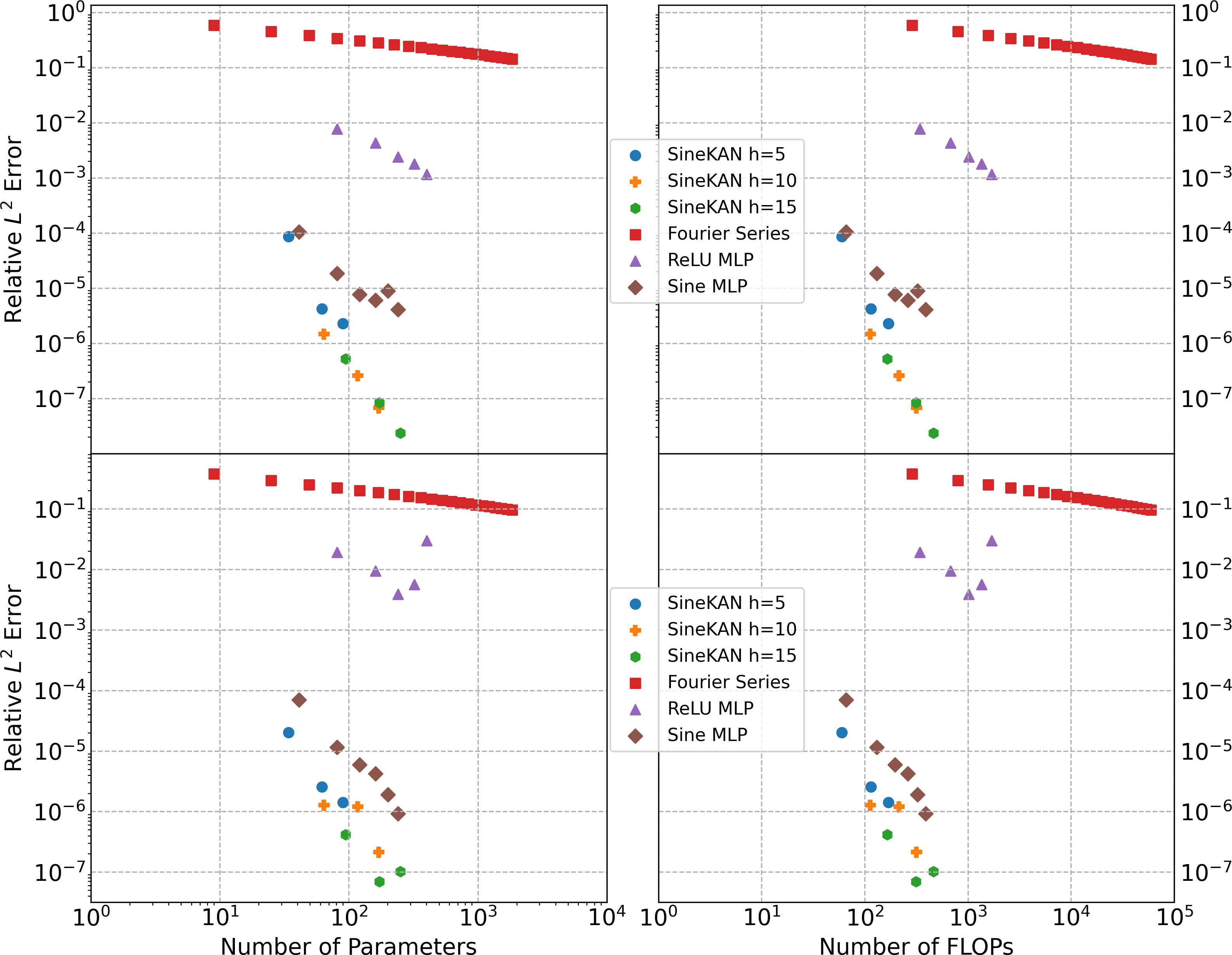
Figure 2: Loss as a function of number of parameters and FLOPs for different tested functions.

Discussion

The findings suggest that SineKAN outperforms classical models, particularly in capturing periodic and time-series data effectively. The sinusoidal functions' periodic nature is inherently suited to such tasks. The model shows significant potential for real-world applications demanding precise function approximations, like signal processing or dynamic predictive modeling.

There is a discussion on the efficiency trade-offs when considering the computational cost of sinusoidal activations versus the more simplified operations used in traditional MLP activations. This has implications for deployment, especially in resource-constrained environments.

Conclusion

The exploration of sinusoidal activation functions in the context of Kolmogorov-Arnold Networks represents a notable advance in neural network design. The demonstrated efficacy of SineKAN underscores its potential as a tool for complex function modeling, with promising avenues for further exploration in dynamic learning environments and applications necessitating high precision. The mathematical foundation provided ensures the robustness of the approach and opens the floor for future enhancement within AI frameworks.

Overall, this paper enriches the discourse on neural network architecture optimization, offering a viable path toward more interpretable and computationally efficient models.