MUR: Momentum Uncertainty guided Reasoning for Large Language Models (2507.14958v1)

Abstract: LLMs have achieved impressive performance on reasoning-intensive tasks, yet optimizing their reasoning efficiency remains an open challenge. While Test-Time Scaling (TTS) improves reasoning quality, it often leads to overthinking, wasting tokens on redundant computations. This work investigates how to efficiently and adaptively guide LLM test-time scaling without additional training. Inspired by the concept of momentum in physics, we propose Momentum Uncertainty-guided Reasoning (MUR), which dynamically allocates thinking budgets to critical reasoning steps by tracking and aggregating stepwise uncertainty over time. To support flexible inference-time control, we introduce gamma-control, a simple mechanism that tunes the reasoning budget via a single hyperparameter. We provide in-depth theoretical proof to support the superiority of MUR in terms of stability and biases. MUR is comprehensively evaluated against various TTS methods across four challenging benchmarks (MATH-500, AIME24, AIME25, and GPQA-diamond) using different sizes of recent Qwen3 models (1.7B, 4B, and 8B). Results demonstrate that MUR reduces computation by over 50% on average while improving accuracy by 0.62-3.37%.

• The paper presents MUR, a training-free method that uses momentum uncertainty to dynamically allocate computational resources during LLM reasoning.
• It introduces a gamma-control mechanism to balance performance and computational cost, achieving up to a 3.37% accuracy improvement and over 50% token savings.
• Experimental results on benchmarks like MATH-500 and AIME demonstrate MUR's superiority over standard Chain-of-Thought and Per-Step Scale methods.

Momentum Uncertainty-Guided Reasoning for LLMs

This paper introduces Momentum Uncertainty-guided Reasoning (MUR), a novel training-free method designed to improve the reasoning efficiency of LLMs during inference. MUR addresses the issue of "overthinking," where LLMs expend computational resources on redundant or unnecessary computations, by dynamically allocating thinking budgets to critical reasoning steps. By modeling LLM reasoning with the concept of momentum, MUR tracks and aggregates step-wise uncertainty over time to identify key steps that require additional computation. The paper includes theoretical proofs supporting MUR's stability and convergence properties and demonstrates its effectiveness across several challenging benchmarks.

Methodological Details

The core innovation of MUR lies in its use of momentum uncertainty to guide the allocation of computational resources during LLM inference. (Figure 1) illustrates the difference between Vanilla CoT, Per-Step Scale, and MUR. The method begins by formulating LLM reasoning as a stepwise auto-regressive process:

$a_t \sim p_\theta(\cdot | x, \mathbf{a}_{<t})$

where $a_t$ represents the generated step at time $t$, $x$ is the input, and $\mathbf{a}_{<t}$ denotes the preceding steps. Test-Time Scaling (TTS) methods are then applied to optimize the reasoning path:

$\hat{a}_t \sim Q(\cdot | x, \mathbf{a}_{<t})$

where $\hat{a}_t$ is the optimized step and $Q$ represents a specific TTS method. To avoid overthinking, MUR introduces a binary detector $D$ that selectively activates TTS based on contextual reasoning dynamics:

$$\hat{a}_t = \begin{cases} Q(\cdot | x, \mathbf{a}_{<t}) &, D(t) = \text{True} \ a_t &, D(t) = \text{False} \end{cases}$$

The detector $D$ is designed to assess the uncertainty of the reasoning trajectory and allocate additional computation to the current step $a_t$ when necessary. Uncertainty is quantified using the average negative log-likelihood of tokens in step $a_t$:

$$m_t = \frac{1}{N} \sum_{j=1}^N -\text{log } p_\theta(a_t^{(j)} | x, \mathbf{a}_{<t}, a_t^{(<j)})$$

Momentum uncertainty, $M_t$, is then calculated recursively to track the overall uncertainty during reasoning:

$M_t = \alpha M_{t-1} + (1 - \alpha) m_t$

where $\alpha \in (0, 1)$ is a hyperparameter that controls the momentum changing. The paper provides theoretical proofs demonstrating that momentum uncertainty is an exponentially weighted sum of step-level uncertainties, which emphasizes recent steps and leads to more stable estimation with lower variance.

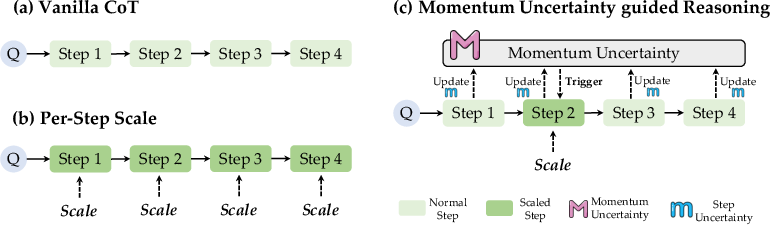
Figure 1: Comparison of reasoning methods. (a) Vanilla CoT: Standard stepwise reasoning without test-time scaling. (b) Per-Step Scale: scales computes per reasoning step. (c) MUR: Adaptive test-time scaling framework (ours).

Scalable Thinking with Gamma-Control

MUR introduces a $\gamma$-control mechanism to balance reasoning performance and computational cost. This mechanism identifies whether the current step is inconsistent with prior reasoning by comparing the step-level uncertainty $m_t$ with the aggregated uncertainty $M_{t-1}$. The detector $D$ is defined as:

$$\hat{a}_t = \begin{cases} Q(\cdot | x, \mathbf{a}_{<t}) &, \text{exp}(m_t) > \text{exp}(M_{t-1}) / \gamma \ a_t &, \text{others} \end{cases}$$

where $\gamma$ is a controllable scaling rate. Smaller $\gamma$ values result in fewer scaled steps, providing flexible control over the computational budget. This $\gamma$-control mechanism is orthogonal to existing TTS methods, allowing MUR to be integrated with various optimization techniques.

Experimental Validation

MUR was evaluated on four challenging benchmarks: MATH-500, AIME24, AIME25, and GPQA-diamond, using different sizes of the Qwen3 models (1.7B, 4B, and 8B). The results demonstrate that MUR reduces computation by over 50% on average while improving accuracy by 0.62–3.37%. The experimental setup involved three test-time scaling methods: Guided Search, LLM as a Critic, and $\phi$-Decoding. Baselines included standard Chain-of-Thought (CoT) reasoning, Per-Step Scale methods, and an average uncertainty baseline.

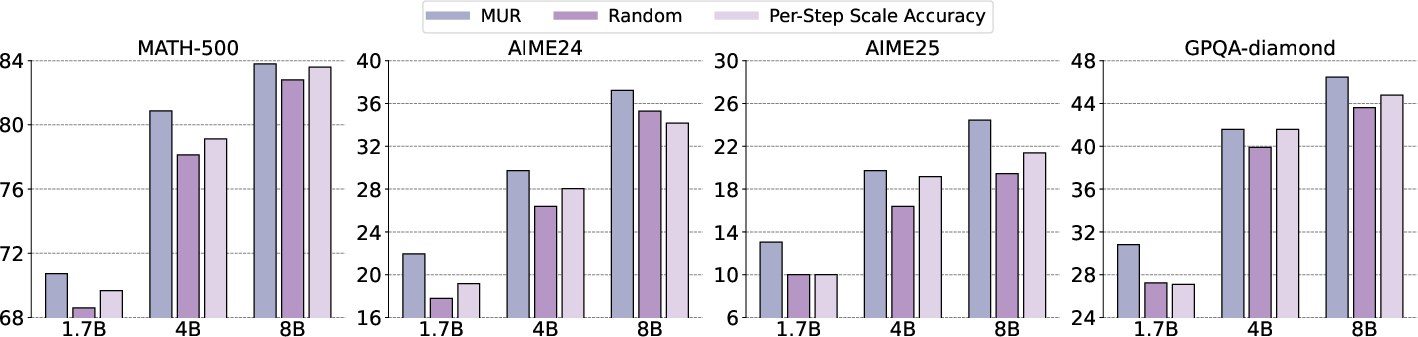
Figure 2: Random scaling accuracy. For each dataset, we average the three test-time scaling reasoning methods (Guided search, LLM as a critic, phi-decoding). X ticks stand for different sizes of Qwen3-series models. Y stands for accuracy.

Results showed that MUR consistently outperformed these baselines, demonstrating its capacity to save tokens while enhancing accuracy. The paper also includes an analysis of the scaling law of $\gamma$-control, demonstrating its ability to balance performance and budget. (Figure 3) illustrates the scaling law of hyperparameter $\gamma$.

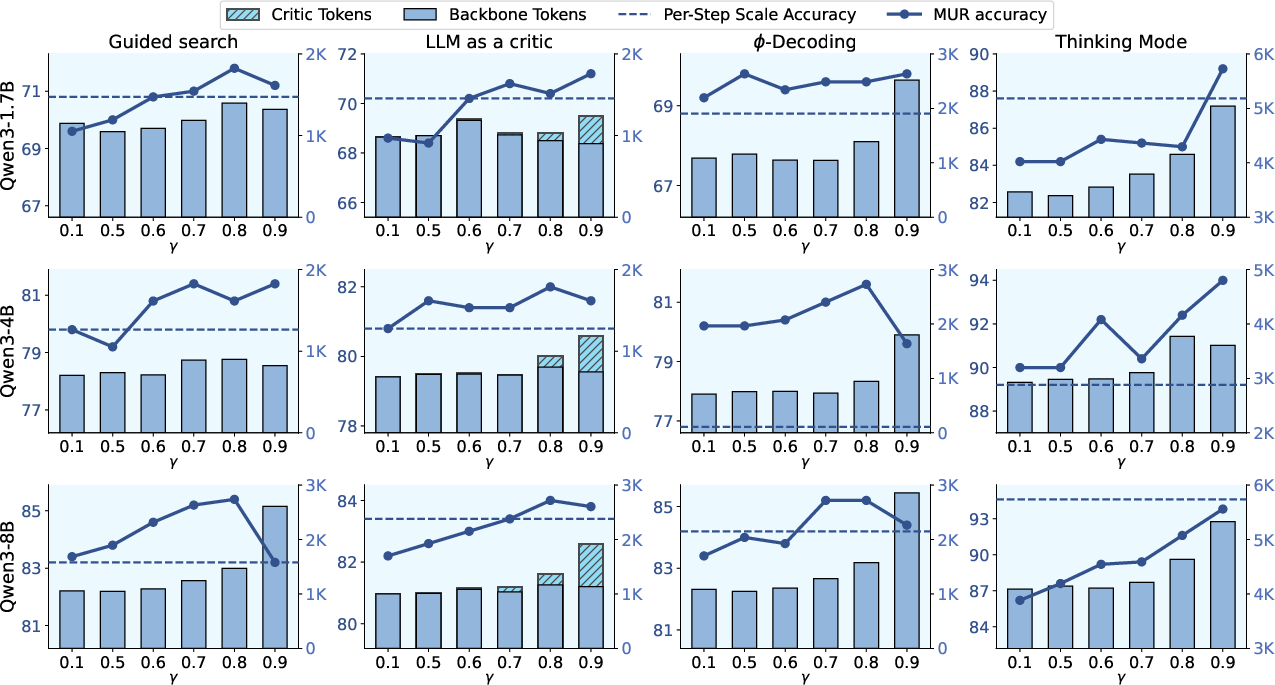
Figure 3: Detail scaling law of gamma. The X axis stands for different values of gamma. The Y axis stands for accuracy. Due to the reason described in Appendix C.1, we additionally report the external model token usage (denoted as Critic Tokens) under LLM as a critic setting to comprehensively reflect the overall computes.

Analysis and Ablation Studies

The paper includes several detailed analyses to support its claims. Step and token usage analysis revealed that MUR scales only a minor portion of steps, and results of random scaling showed that MUR identifies crucial steps to scale. For each setting, the same number of steps are randomly scaled as in Table 1. (Figure 4) shows the impact of changing alpha.

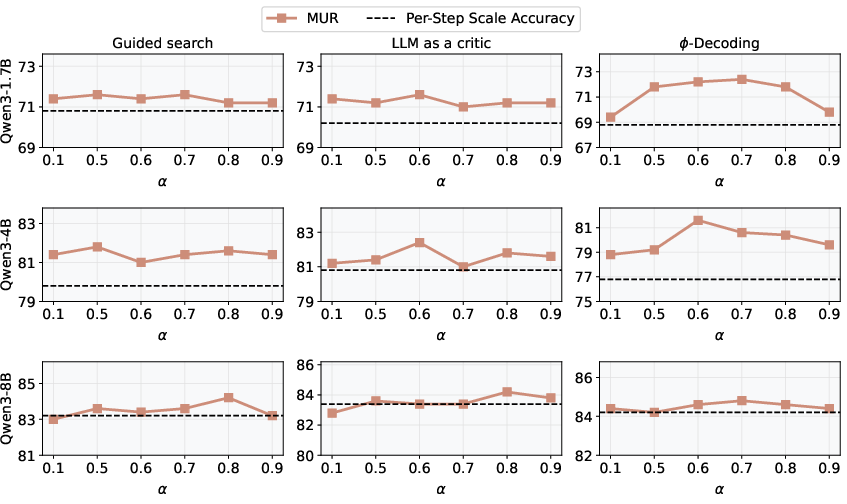
Figure 4: Impact of changing alpha. The X axis stands for different values of alpha. The Y axis stands for accuracy.

Conclusion

The paper makes a strong case for MUR as a computationally efficient method for LLM reasoning. By adaptively allocating computational resources to key reasoning steps, MUR reduces overthinking and improves overall performance. The theoretical grounding of the method, combined with extensive experimental validation, makes a significant contribution to the field. A potential area for future research involves adaptively deciding how much computation to apply to different reasoning steps.