Next-Token Prediction Should be Ambiguity-Sensitive: A Meta-Learning Perspective (2506.16288v1)

Abstract: The rapid adaptation ability of auto-regressive foundation models is often attributed to the diversity of their pre-training data. This is because, from a Bayesian standpoint, minimizing prediction error in such settings requires integrating over all plausible latent hypotheses consistent with observations. While this behavior is desirable in principle, it often proves too ambitious in practice: under high ambiguity, the number of plausible latent alternatives makes Bayes-optimal prediction computationally intractable. Cognitive science has long recognized this limitation, suggesting that under such conditions, heuristics or information-seeking strategies are preferable to exhaustive inference. Translating this insight to next-token prediction, we hypothesize that low- and high-ambiguity predictions pose different computational demands, making ambiguity-agnostic next-token prediction a detrimental inductive bias. To test this, we introduce MetaHMM, a synthetic sequence meta-learning benchmark with rich compositional structure and a tractable Bayesian oracle. We show that Transformers indeed struggle with high-ambiguity predictions across model sizes. Motivated by cognitive theories, we propose a method to convert pre-trained models into Monte Carlo predictors that decouple task inference from token prediction. Preliminary results show substantial gains in ambiguous contexts through improved capacity allocation and test-time scalable inference, though challenges remain.

• The paper introduces MetaHMM and demonstrates that Transformers encounter a 'KL bump' in high-ambiguity contexts.
• It proposes a Monte Carlo predictor that approximates Bayesian integration, effectively mitigating epistemic uncertainty in predictions.
• Experimental results show that the modular approach benefits smaller models, though performance gains diminish as model capacity increases.

Ambiguity Sensitivity in Next-Token Prediction

This paper (2506.16288) addresses the limitations of current autoregressive models in handling ambiguity during next-token prediction. The central hypothesis is that sequence models, which allocate fixed computational resources per token, struggle with high-ambiguity predictions, leading to suboptimal performance. The paper introduces MetaHMM, a synthetic sequence meta-learning benchmark with a tractable Bayesian oracle, to demonstrate this issue and proposes a Monte Carlo predictor to mitigate it.

MetaHMM: A Benchmark for Sequence Meta-Learning

To isolate and analyze the ambiguity problem, the authors introduce MetaHMM, a synthetic environment consisting of a family of Hidden Markov Models (HMMs).

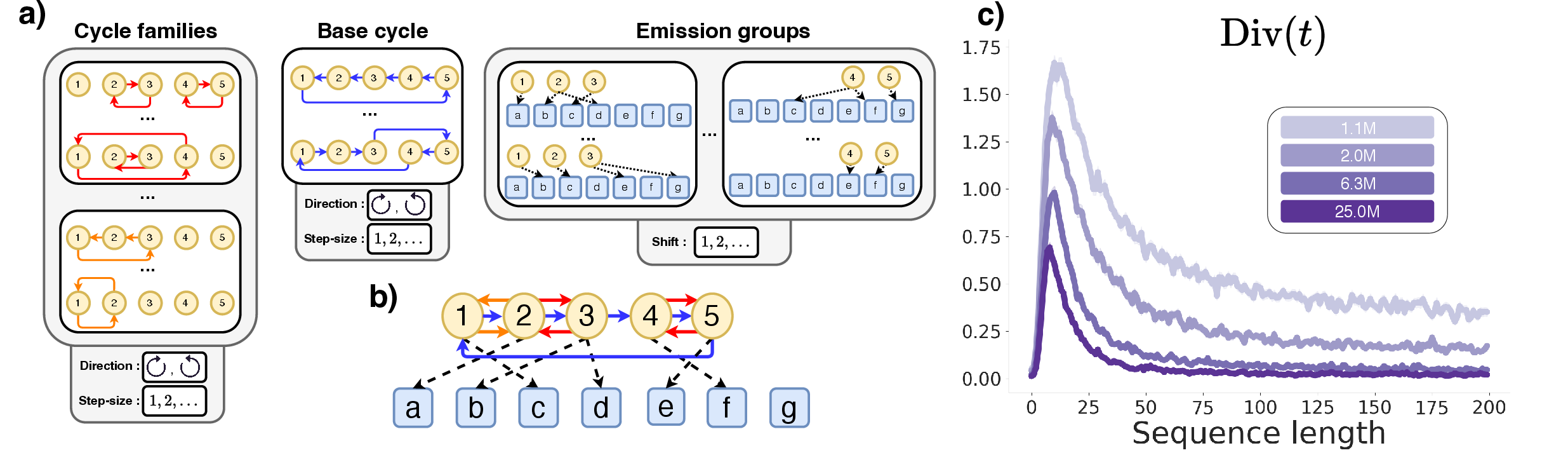
Figure 1: The latent structure of a MetaHMM environment illustrates discrete choices that define an HMM.

Each HMM is defined by a latent code $\bm{\theta}$ that specifies how to construct the HMM from a pool of shared building blocks. This setup allows for efficient and exact computation of the posterior predictive using JAX implementations of the forward algorithm. The ambiguity of $p^*(\theta\mid x_{<t})$ decreases monotonically with sequence length, making the beginning of each sequence a high-ambiguity regime.

Transformers and the KL Bump

The authors train causal Transformer models of varying sizes on MetaHMM environments and evaluate their performance by computing the symmetrized KL divergence between the model's posterior predictive distribution and that of the Bayes-optimal predictor:

$$\text{Div}_x(t) := \frac{1}{2}D_{KL}[p^*(x_t\mid x_{<t})\;\Vert\; p_\phi(x_t\mid x_{<t})] + \frac{1}{2}D_{KL}[ p_\phi(x_t\mid x_{<t}) \;\Vert\; p^*(x_t\mid x_{<t})]$$

The models exhibit a characteristic "KL bump" at short context lengths, indicating that Transformers struggle in regions of high ambiguity. This bump persists across model sizes, suggesting that simply scaling up the model is insufficient to resolve ambiguity-related failures.

Monte Carlo Predictor: A Modular Approach

To address the limitations of Transformers in high-ambiguity settings, the authors propose a modular predictor that approximates the Bayesian integral using a Monte Carlo (MC) estimate.

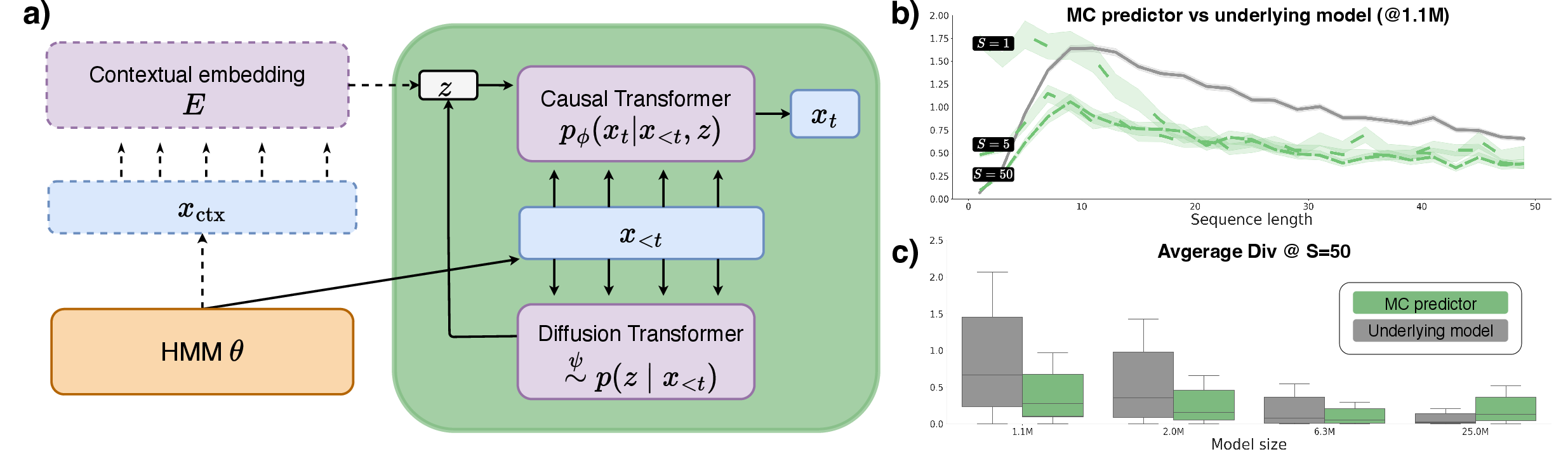
Figure 2: The computational and training structure of the MC predictor separates task inference from token prediction.

This approach involves drawing multiple samples from the task posterior $p(\theta\mid x_{<t})$, computing the conditional predictions $p(x_t\mid x_{<t},\theta)$ for each sample, and averaging the results. The MC predictor separates task inference from token prediction, introducing inductive biases and enabling test-time scaling via the number of samples $S$:

$$p_{\phi,\psi}(x_t\mid x_{<t}) = \frac{1}{S}\sum_{i=1}^S p_\phi(x_t\mid x_{<t},\theta_i) \text{ where } \theta_i \overset{\psi}{\sim} \; p(\theta\mid x_{<t})$$

The method involves training a sequence model $p_\phi$ for unambiguous prediction and a diffusion model to sample latent embeddings $z$ from the context $x_{<t}$.

Results and Discussion

The MC predictor demonstrates improved performance over the original sequence model in high-ambiguity settings, particularly for smaller models. However, the performance gains diminish with larger models, suggesting that the approach is most effective when base models underfit the Bayesian oracle. The authors attribute this to the fact that as model capacity increases, architectural priors matter less.

Conclusion

The paper identifies a structural problem in current sequence modeling approaches: the handling of epistemic uncertainty. The authors propose a modular method that bootstraps a standard autoregressive model into a two-stage predictor, enabling test-time scalable approximate Bayesian inference through Monte Carlo sampling. While challenges remain, this work provides a foundation for future solutions that address the ambiguity problem and improve the robustness and efficiency of foundation models. Future research directions include exploring learned heuristics tailored to ambiguous contexts and mechanisms for information-seeking behavior.