Flowing Datasets with Wasserstein over Wasserstein Gradient Flows (2506.07534v1)

Abstract: Many applications in machine learning involve data represented as probability distributions. The emergence of such data requires radically novel techniques to design tractable gradient flows on probability distributions over this type of (infinite-dimensional) objects. For instance, being able to flow labeled datasets is a core task for applications ranging from domain adaptation to transfer learning or dataset distillation. In this setting, we propose to represent each class by the associated conditional distribution of features, and to model the dataset as a mixture distribution supported on these classes (which are themselves probability distributions), meaning that labeled datasets can be seen as probability distributions over probability distributions. We endow this space with a metric structure from optimal transport, namely the Wasserstein over Wasserstein (WoW) distance, derive a differential structure on this space, and define WoW gradient flows. The latter enables to design dynamics over this space that decrease a given objective functional. We apply our framework to transfer learning and dataset distillation tasks, leveraging our gradient flow construction as well as novel tractable functionals that take the form of Maximum Mean Discrepancies with Sliced-Wasserstein based kernels between probability distributions.

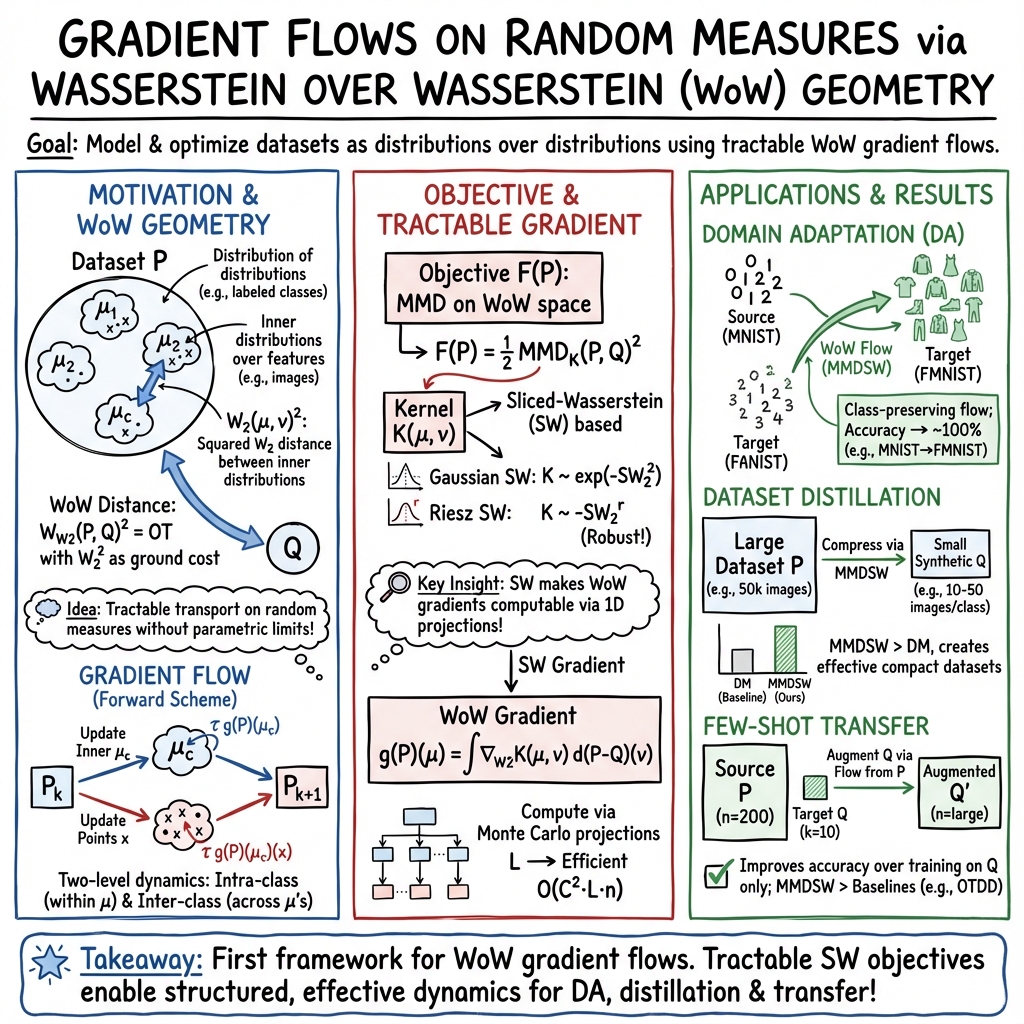
• The paper introduces a novel framework that models labeled datasets as distributions over distributions using the WoW distance.
• It constructs tractable gradient flows in infinite-dimensional probability spaces to achieve smooth dataset transformations.
• Experiments demonstrate effective domain adaptation and dataset distillation via Sliced-Wasserstein-based MMD functionals on image datasets.

Flowing Datasets with Wasserstein over Wasserstein Gradient Flows

Introduction

The article "Flowing Datasets with Wasserstein over Wasserstein Gradient Flows" (2506.07534) addresses a novel challenge in machine learning by focusing on the manipulation of datasets represented as probability distributions, specifically within the context of gradient flows in probability distribution spaces. It introduces the concept of representing labeled datasets as distributions over distributions, utilizing the optimal transport framework to establish a metric structure known as the Wasserstein over Wasserstein (WoW) distance. This paper provides a comprehensive methodology for developing tractable gradient flows on these infinite-dimensional spaces, which is pivotal for applications like domain adaptation, transfer learning, and dataset distillation.

Methodology

The authors propose a framework where each class in a dataset is viewed as a conditional distribution of features, and the entire dataset is modeled as a mixture of these distributions. This results in the interpretation of labeled datasets as distributions over probability distributions. The space is endowed with the WoW distance, which builds on the Wasserstein-2 metric from optimal transport, and a differentiation structure is established to facilitate the definition of WoW gradient flows.

WoW gradient flows are constructed to operate in this space, enabling a decrease in desirable objective functionals. The authors apply these flows to tasks like transfer learning and dataset distillation, utilizing novel tractable functionals structured as Maximum Mean Discrepancies (MMD) with kernels based on the Sliced-Wasserstein distance. This approach allows the framework to address the main challenge of evolving datasets within this complex probabilistic framework effectively.

Experiments

The paper includes detailed experiments demonstrating the practical utility of the proposed gradient flow methodology. It shows how distributions of one dataset can be smoothly transitioned to another, as evidenced by structured transformations between image datasets such as MNIST and Fashion-MNIST.

Figure 1: Samples along the flow from MNIST to FMNIST (Left), KMNIST (Middle), and USPS (Right).

The authors employ a unique combination of WoW gradient flows with Sliced-Wasserstein-based MMDs to perform experiments on image datasets by simulating transitions of class distributions. This structured transition ensures that distributions from one class in a source dataset translate meaningfully to another class in a target dataset, confirming the robustness of the approach in preserving class integrity throughout the flow process.

Further experiments explore domain adaptation, employing a pretrained classifier on data flowed from FMNIST to MNIST to verify the accuracy of the domain adaptation task.

Figure 2: Accuracy of the pretrained classifiers along the flow from FMNIST (Left) and SVHN (Right) towards MNIST and CIFAR10.

The findings suggest that the framework not only preserves key statistical properties but achieves accurate domain transitions, validating the theoretical claims.

Conclusion

The paper proposes a robust theoretical framework and practical implementation of utilizing Wasserstein over Wasserstein gradient flows to manipulate datasets represented as distributions over distributions. This approach effectively addresses challenges in domain adaptation and dataset distillation by providing a systematic method for transferring dataset characteristics across distinct domains. The research offers extensive empirical evidence, illustrating that the devised WoW gradient flows perform efficiently in practice, capturing essential inter-class properties during redistribution.

In summary, this paper lays critical groundwork in optimizing functionals over spaces of probability measures on probability measures, with substantial implications for advancing machine learning applications requiring domain adaptation and dataset condensation. Future directions could explore extending these concepts to broader classes of functional objectives or more complex manifold structures.