A Theoretical Framework for Prompt Engineering: Approximating Smooth Functions with Transformer Prompts (2503.20561v1)

Abstract: Prompt engineering has emerged as a powerful technique for guiding LLMs toward desired responses, significantly enhancing their performance across diverse tasks. Beyond their role as static predictors, LLMs increasingly function as intelligent agents, capable of reasoning, decision-making, and adapting dynamically to complex environments. However, the theoretical underpinnings of prompt engineering remain largely unexplored. In this paper, we introduce a formal framework demonstrating that transformer models, when provided with carefully designed prompts, can act as a configurable computational system by emulating a ``virtual'' neural network during inference. Specifically, input prompts effectively translate into the corresponding network configuration, enabling LLMs to adjust their internal computations dynamically. Building on this construction, we establish an approximation theory for $\beta$-times differentiable functions, proving that transformers can approximate such functions with arbitrary precision when guided by appropriately structured prompts. Moreover, our framework provides theoretical justification for several empirically successful prompt engineering techniques, including the use of longer, structured prompts, filtering irrelevant information, enhancing prompt token diversity, and leveraging multi-agent interactions. By framing LLMs as adaptable agents rather than static models, our findings underscore their potential for autonomous reasoning and problem-solving, paving the way for more robust and theoretically grounded advancements in prompt engineering and AI agent design.

• The paper introduces a framework that demonstrates how engineered prompts allow transformers to emulate virtual neural networks.
• It establishes precise approximation bounds, showing that longer and diverse prompts significantly reduce error in approximating smooth functions.
• The study validates empirical prompting techniques and suggests that prompt optimization improves computational efficiency in large language models.

A Theoretical Framework for Prompt Engineering: Approximating Smooth Functions with Transformer Prompts (2503.20561)

Introduction

The paper "A Theoretical Framework for Prompt Engineering: Approximating Smooth Functions with Transformer Prompts" (2503.20561) develops a formal framework to understand how prompt engineering can enhance the computational capabilities of LLMs, with a specific focus on transformers. While LLMs have shown proficiency in a wide range of natural language processing tasks, their potential reaches beyond text-based applications, increasingly positioning them as general-purpose reasoning engines.

Theoretical Foundations of Prompt Engineering

Despite the practical success of prompt engineering, its theoretical underpinnings have been less explored. The paper fills this gap by demonstrating that transformer models can act as configurable computational systems when supplied with well-structured prompts. Essentially, a well-designed prompt allows a transformer to dynamically emulate a "virtual" neural network during inference, adjusting its internal computations accordingly. This framework allows transformers to approximate $\beta$-times differentiable functions with arbitrary precision, thereby converting theoretical constructs into tangible solutions (Figure 1).

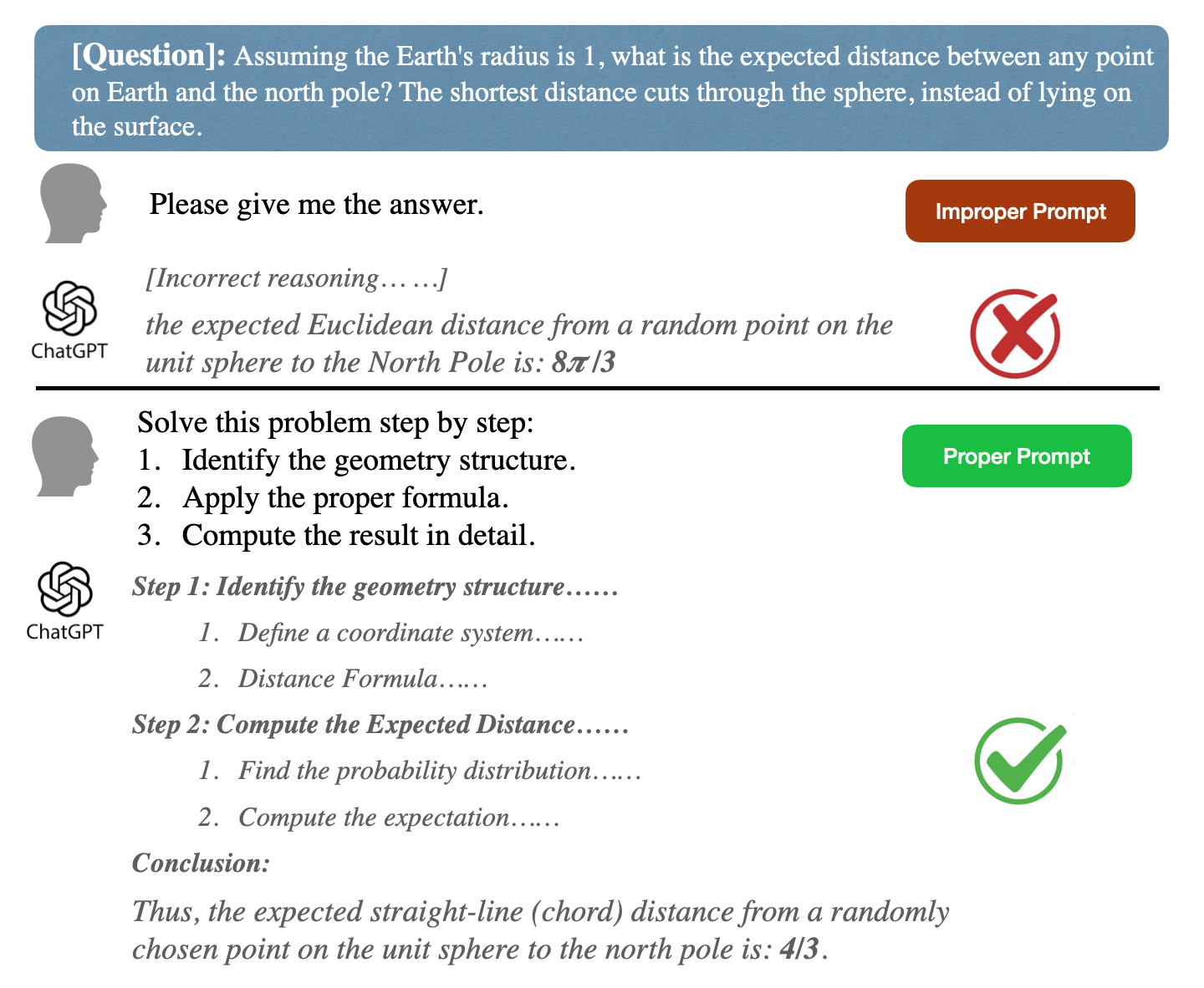
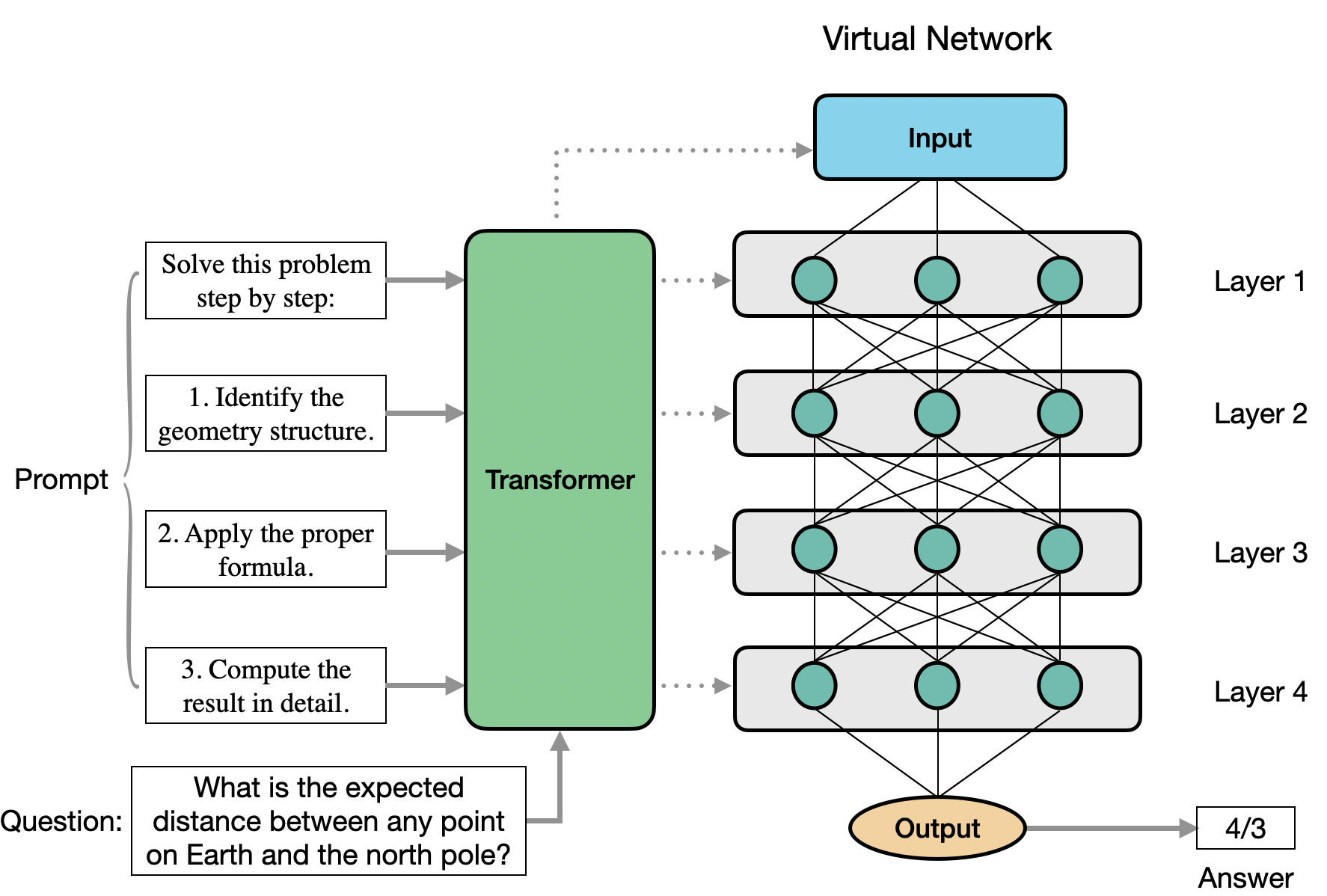
Figure 1: Left: Example of prompt engineering. The responses are collected from GPT-4o, and the detailed computations are omitted for simplicity. Proper prompt design can improve the reasoning ability of LLM generations. Right: Illustration of our theory. Transformer can emulate a ``virtual'' neural network based on the prompts to execute a given task.

Transformers as Virtual Neural Networks

Model Architecture

The work describes transformers as comprising two main types of layers: self-attention and feed-forward transformation. The self-attention mechanism focuses on inter-token relationships without being influenced by position, utilizing query, key, and value components for projection. The feed-forward layers apply non-linear transformations to each token independently to capture complex interactions.

Emulating Neural Networks

The paper demonstrates that LLMs can emulate a "virtual" deep neural network by parsing input prompts into network configurations dynamically, emulating a configuration that acts on input data with high expressivity for smooth functions. This approach is not constrained to Lipschitz continuous functions but extends to $\beta$-times differentiable functions.

The paper further elaborates using corollaries based on Theorem 3.1 denoting the possibility of approximating such smooth functions effectively with carefully structured prompts provided to the transformers. Interestingly, the emulation shows that the internal structure of transformers allows them to act as deep neural networks, with prompts effectively encoding adjustable network configurations.

Approximation Bounds for Smooth Functions

The paper extends existing theories on transformers and neural nets to provide approximation bounds for smooth functions. It discusses the role of prompt length and prompt diversity in the feasibility and precision of function approximation, offering mathematical bounds for these scenarios.

Corollary 3.2 posits that the approximation error scales with the prompt length $T$ and the depth $L$ as $\tilde{O}(T^{-2\beta/p})$, supporting the idea that longer prompts enhance the capability of transformers to emulate neural networks. Furthermore, it discusses the ability of transformers to approximate continuous functions when the first feed-forward layer's activation is replaced with an Elementary Universal Activation Function (EUAF). The transformation to EUAF significantly reduces the necessary token length, demonstrating the role of activation functions in function approximation.

Insights into Empirical Prompting Techniques

The theoretical framework provides insights into several empirically successful prompt engineering practices:

1. Longer Prompts Enhance Expressivity: Longer and detailed prompts enhance model expressivity and performance, supporting empirical observations that more informative prompts result in improved LLM outputs. The mathematical bounds derived in Corollary 4.1 corroborate these findings.
2. Filtering Out Irrelevant Information: Studies have evidenced that irrelevant content within prompts impairs model performance. The paper theoretically models irrelevant tokens as random noise, demonstrating constant lower bounds on approximation errors with noisy prompts, aligning with empirical observations.
3. Prompt Diversity Increases Capacity: Diverse prompt structures have been shown to improve model performance. Corollary 4.3 theoretically substantiates this by linking prompt diversity with increased virtual network weight rank, reducing approximation errors.
4. Multi-Agent Collaboration: The paper discusses how structured multi-agent prompting strategies refine task decomposition, reducing approximation errors and improving LLM performance for complex reasoning tasks.

Conclusion

The paper frames prompt design as a critical factor in harnessing transformers' capacity to emulate neural networks, offering a robust theoretical basis for empirically driven prompt engineering practices. Through the derivation of approximation error bounds and the discussion of prompt structures and strategies, the research provides guidelines for optimizing LLM behavior. These insights pave the way for future explorations into computational efficiency, specifically regarding prompt structuring strategies that maximize performance without needing to increase model scale. Future research can explore the extension of these ideas to diverse AI systems and adaptive inference strategies that adjust model reasoning depth in real-time.