Prompt Engineering Through the Lens of Optimal Control (2310.14201v2)

Abstract: Prompt Engineering (PE) has emerged as a critical technique for guiding LLMs in solving intricate tasks. Its importance is highlighted by its potential to significantly enhance the efficiency and effectiveness of human-machine interaction. As tasks grow increasingly complex, recent advanced PE methods have extended beyond the limitations of single-round interactions to embrace multi-round interactions, which allows for a deeper and more nuanced engagement with LLMs. In this paper, we propose an optimal control framework tailored for multi-round interactions with LLMs. This framework provides a unified mathematical structure that not only systematizes the existing PE methods but also sets the stage for rigorous analytical improvements. Furthermore, we extend this framework to include PE via ensemble methods and multi-agent collaboration, thereby enlarging the scope of applicability. By adopting an optimal control perspective, we offer fresh insights into existing PE methods and highlight theoretical challenges that warrant future research. Besides, our work lays a foundation for the development of more effective and interpretable PE methods.

• The paper presents a novel framework that models prompt engineering as an optimal control problem for multi-round interactions with LLMs.
• It employs random search and reinforcement learning methods to navigate the discrete nature of language and optimize responses.
• The approach paves the way for ensemble and multi-agent strategies, addressing variability and computational challenges in prompt engineering.

Prompt Engineering Through the Lens of Optimal Control

Introduction

"Prompt Engineering Through the Lens of Optimal Control" proposes a novel framework for understanding prompt engineering (PE) in LLMs as a control problem. The framework uses optimal control theory to provide a unified mathematical structure to analyze and optimize multi-round prompt interactions. Unlike traditional single-round prompting, multi-round prompting allows for more complex and nuanced interactions with LLMs, enhancing their problem-solving capabilities.

General Framework

Concepts and Terminologies

In this paper, prompts are considered stimuli or queries that initiate interactions with LLMs. The LLM processes these prompts and produces responses that ideally meet certain desired outcomes or evaluations. In multi-round interactions, the sequence of prompts allows a dynamic back-and-forth, refining the LLM's responses through cascading prompts that build upon previous exchanges.

PE is conceptualized as formulating and solving an optimal control problem, where the goal is to design a sequence of prompts that maximizes a defined performance metric or evaluation function. The optimal control perspective helps unify various existing PE strategies within a coherent analytical framework.

Figure 1: The general framework of multi-round PE. In our optimal control formulation \eqref{def:PE_basic}, the task (or query) is denoted by $z^q$, and the prompt candidate sets expand as interactions progress.

Potentials and Challenges in Prompt Engineering

Potentials

The proposed framework reveals potential for more effective PE through iterative refinement. It leverages the inherent variability and vast knowledge base of LLMs. This iterative refinement process can bridge the gap between variable responses and targeted outputs by modeling LLMs as stochastic samplers that can approximate user desired knowledge distributions over repeated interactions.

Challenges

Challenges include formulating appropriate evaluation functions and prompt candidate sets due to the discrete, structured nature of language. Furthermore, the inherent complexity of LLM dynamics, treated as black boxes, complicates optimization in continuous spaces; hence, gradient-free optimization techniques become necessary. These requirements highlight theoretical gaps and computational constraints, necessitating further exploration.

Prompt Engineering Methods

Enlarging the Prompt Candidate Set

Methods like Progressive-Hint Prompting (PHP) and Least-to-Most (LtM) illustrate techniques to expand the prompt candidate set during interactions. PHP uses previous responses to guide future prompts for arithmetic tasks, while LtM employs a structured decomposition approach to break tasks into more manageable sub-tasks for reasoning tasks.

Figure 2: An example of PHP interactions. PHP uses iterative prompt modifications based on previous outputs to support task completion.

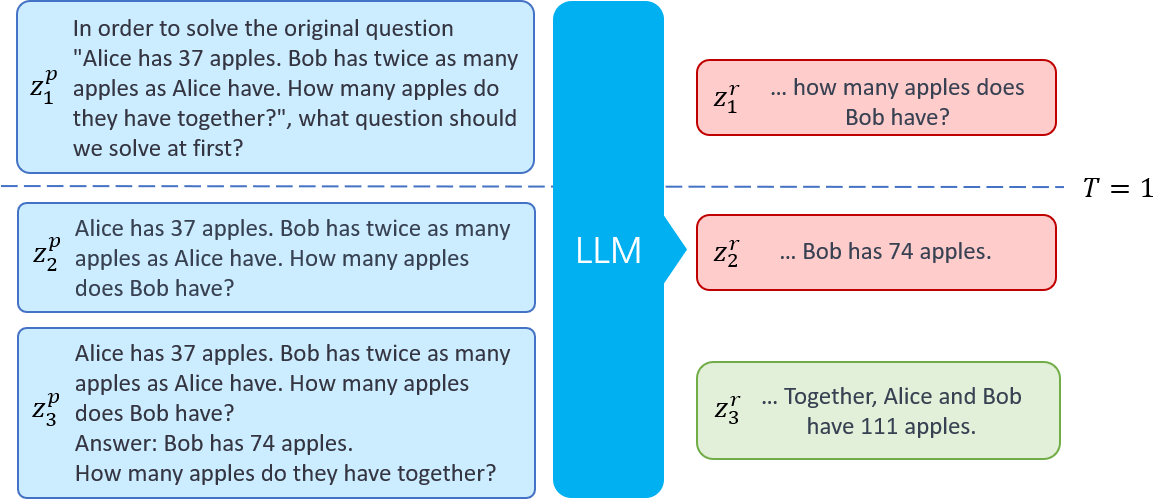
Figure 3: An example of LtM interactions with $T=1$. LtM decomposes complex tasks into simpler steps for sequential solution generation.

Optimizing Prompts

Random Search Methods

APE and Tree of Thought (ToT) are examples of employing random search to optimize prompts. These methods explore candidate prompts through systematic evaluation of variability within the LLM's outputs, though they may require reliable priors and substantial computational cost.

Reinforcement Learning Methods

RLPrompt and PromptPG demonstrate the application of reinforcement learning in optimizing prompts. Model-free RL aligns with the opaque nature of LLMs, effectively optimizing PE despite the computational challenges inherent in exploration and feedback-based refinement.

Further Extensions

Prompt Engineering via Ensemble Methods

Ensemble methods utilize stochastic variations in LLM responses to improve result robustness and accuracy. By framing these as part of the optimal control setup, methods like Self-Consistency CoT can be systematically understood and leveraged to address variability in PE outcomes.

Prompt Engineering via Multi-Agent Collaboration

Multi-agent systems distribute tasks among multiple LLMs, each aligned with different initial instructions. This setup allows for diverse strategies and capabilities to be employed and optimized collaboratively, extending the applicability of PE beyond single-agent scenarios.

Conclusions

The paper introduces a comprehensive control-theoretical framework that systematizes and extends existing methods for multi-round prompt engineering. It lays the groundwork for innovative PE approaches by unifying disparate strategies under a mathematically rigorous system, which could illuminate pathways for extensive empirical and theoretical exploration in optimizing interactions with LLMs.