Random Scaling for Emergent Capabilities (2502.17356v4)

Abstract: LLMs famously improve under a smooth scaling law, but some specific capabilities exhibit sudden breakthroughs in performance. While advocates of "emergence" view breakthroughs as unlocked capabilities, others attribute them to thresholding effects on noncontinuous metrics. We propose that breakthroughs are instead driven by continuous changes in the probability distribution of training outcomes when performance is bimodally distributed across random seeds. In synthetic length generalization tasks, we show that different random seeds can produce either highly linear or emergent scaling trends. We reveal that sharp breakthroughs in metrics are produced by underlying continuous changes in their distribution across seeds. In a case study of inverse scaling, we show that even as the probability of a successful run declines, the average performance of a successful run increases monotonically. We validate our distributional scaling framework on realistic settings by measuring MMLU performance in LM populations. Our observations hold true even under continuous loss metrics, confirming that random variation must be considered when predicting a model's performance from its scale.

• The paper shows that random scaling leads to bimodal performance distributions, revealing genuine breakthroughs beyond linear scaling in LMs.
• It employs synthetic tasks and reinitialized MMLU experiments to quantify emergent capabilities using metrics like breakthroughness and NLL loss.
• The results challenge current theories by attributing sudden performance jumps to stochastic training variations rather than measurement artifacts.

Detailed Analysis of "Random Scaling for Emergent Capabilities" (2502.17356)

Introduction

The paper "Random Scaling for Emergent Capabilities" explores how LMs exhibit sudden breakthroughs in specific capabilities, challenging the traditional understanding of smooth scaling laws. The authors argue that these breakthroughs are not merely stochastic artifacts or measurement issues but are driven by genuine multimodal distributions in model performance. This essay will discuss the experimental methodologies, results, and implications of this paper, focusing on synthetic length generalization tasks and real-world LM benchmarks like the MMLU.

Synthetic Length Generalization Tasks

Task Definitions and Setup

The paper employs two synthetic tasks to investigate the phenomenon of emergent capabilities: the count task and reverse order addition with index hints. These tasks are selected due to their requirement for compositional reasoning, a trait linked to emergent capability in models. Transformer models are trained with varying depths and widths to understand the impact of model scale.

Emergence and Bimodality

The paper finds that performance distributions are bimodal across different training seeds. This bimodality explains why some models exhibit breakthroughs while others exhibit linear scaling with model size. For instance, in the count task, the performance across seeds results in distinctly separate clusters of high and low performing groups, suggesting that breakthroughs at specific scales are indeed stochastic yet genuinely represent learning new capabilities (Figure 1).

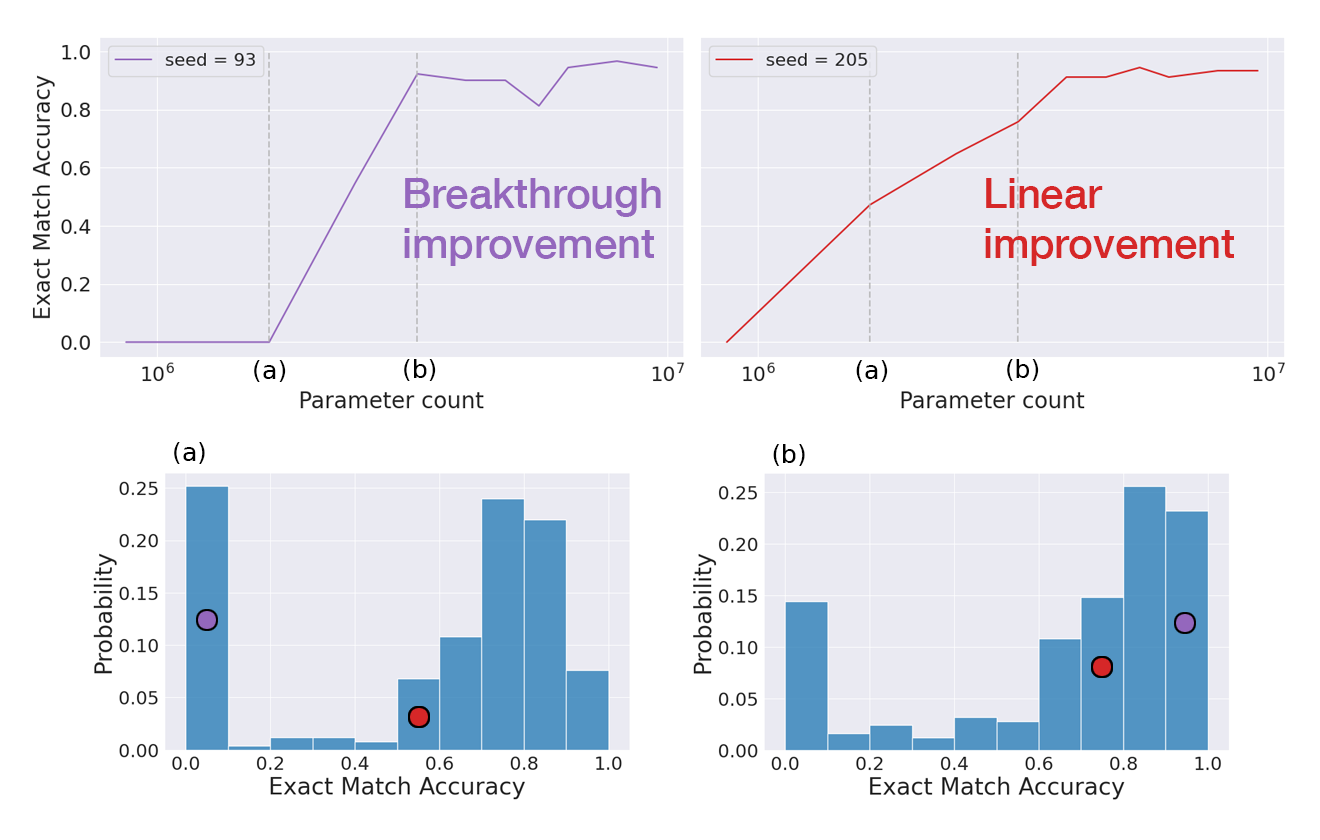
Figure 1: Different random seeds produce different scaling trends. Scaling trends can be emergent or linear for different seeds, even if all models train on the same data with the same hyperparameters.

Statistical Analysis

The paper employs metrics like breakthroughness and linearity to quantify the nature of emergent capabilities. The analysis shows sudden breakthroughs are not artifacts of evaluation but are due to changes in the probability distributions across seeds. This observation supports the argument against the mirage hypothesis, which attributes emergent properties to measurement artifacts.

LLM Experiments

MMLU Benchmark Analysis

Using the MMLU benchmark, the paper validates the findings from synthetic tasks in real-world scenarios. By reinitializing model layers and retraining, the authors simulate new training seeds for large-scale LMs. Results confirm that performance on multiple-choice tasks like MMLU is also bimodally distributed, with some initialization leading to successful relearning of task formats while others do not (Figure 2).

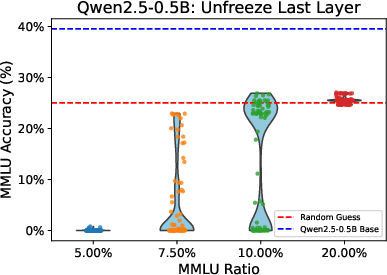
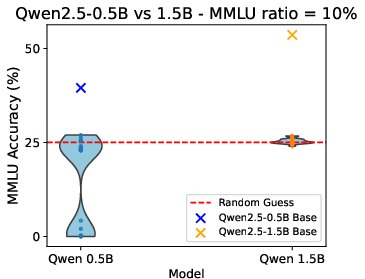
Figure 2: Performance on MMLU. Different seeds lead to bimodally distributed performance, with enough MMLU data, all models score above the random baseline.

Continuous Metrics and Emergence

The paper further investigates whether bimodal emergence is an artifact of discrete metrics. The paper shows that continuous metrics, like negative log likelihood (NLL), also exhibit multimodal distributions, confirming that observed emergences are not entirely due to thresholding effects. For instance, using maximum per-token loss as a continuous measure still results in bimodal distributions (Figure 3).

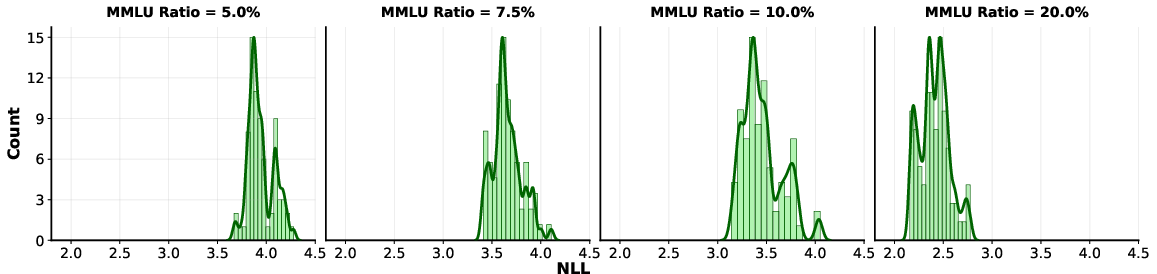
Figure 3: NLL loss distributions on the MMLU test set. Each distribution is provided as a histogram and as a smoothed KDE.

Implications and Discussion

Theoretical Implications

The findings challenge the current narratives regarding emergent capabilities. The paper argues that both the emergence and mirage camps must consider the role of random variation and multimodal distribution in model performance. The results imply that emergent capabilities may not always be tied to model size but could be due to the probabilistic nature of capability acquisition.

Practical Considerations

From a practical standpoint, the paper highlights the importance of considering random variation in performance predictions of LMs. As training multiple seeds at large scales is costly, understanding these statistical underpinnings can lead to more robust model evaluation and deployment strategies.

Conclusion

The "Random Scaling for Emergent Capabilities" paper sheds light on how LLMs exhibit emergent capabilities through the lens of stochasticity and probabilistic distributions. By rigorously analyzing both synthetic and real-world tasks, the research reveals that emergent capabilities are not just artifacts but are deeply tied to underlying stochastic processes in model training. These insights are crucial for advancing our understanding of scaling laws and designing future robust and capable machine learning architectures.