Straight to Zero: Why Linearly Decaying the Learning Rate to Zero Works Best for LLMs (2502.15938v1)

Abstract: LLMs are commonly trained with a learning rate (LR) warmup, followed by cosine decay to 10% of the maximum (10x decay). In a large-scale empirical study, we show that under an optimal peak LR, a simple linear decay-to-zero (D2Z) schedule consistently outperforms other schedules when training at compute-optimal dataset sizes. D2Z is superior across a range of model sizes, batch sizes, datasets, and vocabularies. Benefits increase as dataset size increases. Leveraging a novel interpretation of AdamW as an exponential moving average of weight updates, we show how linear D2Z optimally balances the demands of early training (moving away from initial conditions) and late training (averaging over more updates in order to mitigate gradient noise). In experiments, a 610M-parameter model trained for 80 tokens-per-parameter (TPP) using D2Z achieves lower loss than when trained for 200 TPP using 10x decay, corresponding to an astonishing 60% compute savings. Models such as Llama2-7B, trained for 286 TPP with 10x decay, could likely have saved a majority of compute by training with D2Z.

• The paper demonstrates that the D2Z schedule consistently reduces validation loss, achieving an approximate 0.77% gain over cosine decay in 610M-parameter models.
• It shows that D2Z scales more effectively with higher training tokens per parameter, particularly mitigating gradient noise in later training stages.
• The study explains that D2Z works by optimally balancing bias and variance in the AdamW optimizer through an extended EMA perspective, leading to improved training efficiency.

Straight to Zero: Why Linearly Decaying the Learning Rate to Zero Works Best for LLMs

Introduction

The paper "Straight to Zero: Why Linearly Decaying the Learning Rate to Zero Works Best for LLMs" explores the efficacy of the linear decay-to-zero (D2Z) learning rate schedule for training LLMs, emphasizing its superiority over traditional cosine decay schedules. This empirical study evaluates various learning rate (LR) schedules across different model and dataset scales, demonstrating that D2Z consistently results in lower validation loss when tuned optimally, especially in high-compute-efficient scenarios. Furthermore, the study introduces a novel perspective on AdamW optimizer as an exponentially weighted moving average of weight updates, providing insights into why linear decay effectively balances the demands of bias and variance reduction during training.

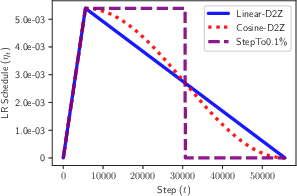
*Figure 1: LR schedules and their update-combination duals: Each LR schedule, eta_t (left) and weight decay, lambda, implies a weighted combination of weight updates, with combination coefficients $c_{t,i}$. *

Results and Analysis

Optimal Learning Rate Schedule

The experiments conducted on 610M-parameter models at 20 TPP demonstrate that D2Z consistently yields lower validation loss than the traditional 10% cosine decay, with an approximate 0.77% decrease in loss at optimal settings. This finding is consistent across various peak learning rates and model architectures, including when using the standard parameterization, which further supports D2Z’s robust adaptability across different training conditions.

Impact of Training Duration and Model Scale

For smaller TPPs, D2Z initially underperforms compared to the 10% decay. However, its relative advantage increases with the number of training tokens per parameter (TPP), suggesting that linear decay is particularly beneficial during later stages of training characterized by high gradient noise. The scalability of this approach is highlighted across model sizes, with improvements more pronounced at larger scales, indicating a growing performance gap in favor of D2Z as model size increases (Figure 2).

(Figure 2)

Figure 2: Loss gap between D2Z and 10 grows with TPP for 111M, 610M, and 1.7B-scale models.

Mechanism of Linear Decay’s Success

The paper provides a theoretical underpinning for D2Z’s effectiveness through an extended EMA perspective. In AdamW, parameters are viewed as a convex combination of past weight updates, where linear decay optimally averages across updates, reducing variance without markedly increasing bias. The study emphasizes that the key to D2Z's success lies in its capacity to modulate gradient noise more efficiently than cosine decay, especially as dataset sizes grow.

Figure 3: Comparison across batch sizes (iso-TPP) (610M): As batch size decreases, the optimal LR drifts significantly lower for 10 decay, less so for D2Z.

Experimental Validation

The empirical results validate the theoretical model by comparing D2Z with other continuous schedules such as Warmup-Stable-Decay (WSD) and cyclic LR, where D2Z consistently surpasses these models at equivalent computational budgets. Furthermore, tests varying batch sizes and sparsity confirm that D2Z maintains superior performance by offering more stable learning rates and reducing validation loss variance across different training setups.

Conclusion

The study convincingly argues for adopting linear decay-to-zero as the LR schedule of choice when training LLMs. Its strength lies in balancing the bias-variance trade-off effectively, yielding substantial computational savings and better model performance, particularly as models scale. As a result, D2Z is poised to be integral to improving LLM training efficiencies, especially in resource-constrained environments.

Future Prospects

While the benefits of D2Z are robust across various parameters and configurations, future research should explore its application to different optimizer variants and investigate its interaction with advanced regularization techniques. Additionally, extending this approach to other domains where training dynamics resemble those of LLMs could further validate its universality and efficacy.