Modern Hopfield Networks with Continuous-Time Memories (2502.10122v4)

Abstract: Recent research has established a connection between modern Hopfield networks (HNs) and transformer attention heads, with guarantees of exponential storage capacity. However, these models still face challenges scaling storage efficiently. Inspired by psychological theories of continuous neural resource allocation in working memory, we propose an approach that compresses large discrete Hopfield memories into smaller, continuous-time memories. Leveraging continuous attention, our new energy function modifies the update rule of HNs, replacing the traditional softmax-based probability mass function with a probability density, over the continuous memory. This formulation aligns with modern perspectives on human executive function, offering a principled link between attractor dynamics in working memory and resource-efficient memory allocation. Our framework maintains competitive performance with HNs while leveraging a compressed memory, reducing computational costs across synthetic and video datasets.

• The paper introduces a continuous-time memory mechanism that significantly boosts storage efficiency and retrieval performance for Hopfield Networks.
• It replaces discrete fixed-point attractors with compressed continuous-time representations using basis functions and attention mechanisms.
• Numerical experiments on synthetic and video datasets confirm competitive performance with reduced computational load and enhanced scalability.

Modern Hopfield Networks with Continuous-Time Memories

Introduction

The paper "Modern Hopfield Networks with Continuous-Time Memories" (2502.10122) presents a novel architecture for Hopfield Networks (HNs), aiming to improve memory storage efficiency by using continuous-time representations. Traditional HNs associate memories as discrete fixed-point attractors, typically suffering from linear scalability issues in terms of storage capacity. Inspired by psychological theories of continuous neural resource allocation, this paper proposes compressing large discrete memories into smaller, continuous-time forms. This approach fuses continuous attention mechanisms with modern Hopfield energy functions, resulting in an efficient and resource-conscious memory representation.

Background and Motivation

Hopfield Networks traditionally utilize memory matrices for associative recall, with storage capacity scaling linearly with input dimensionality. Recent advancements have enhanced this to super-linear capacities through stronger nonlinear update rules. However, these improvements often fail to address memory efficiency concerns. The paper draws inspiration from psychological theories suggesting continuous allocation of neural resources for memory representation, contrasting with traditional slot-based models of memory. The integration of continuous attention aims to reflect more realistically the dynamics observed in human cognitive processes.

Continuous-Time Memory and Architecture

The proposed architecture modifies the Hopfield energy function by leveraging continuous-time signals through basis functions and continuous query-key similarities. The authors introduce a continuous-time memory mechanism characterized by:

• Continuous Attention Framework: By defining attention weights over continuous signals, the framework avoids inefficient fixed-rate sampling. Instead, it uses a probability density function over continuous functions to offer a more flexible model fitting for long and unbounded sequences.
• Energy Function Update: The new energy function replaces discrete memory representations using compressed alternatives derived from basis functions, substantially decreasing the computational load while maintaining retrieval performance.

This continuous framework effectively transforms the storage mechanism in Hopfield Networks, promoting a more scalable and memory-efficient system.

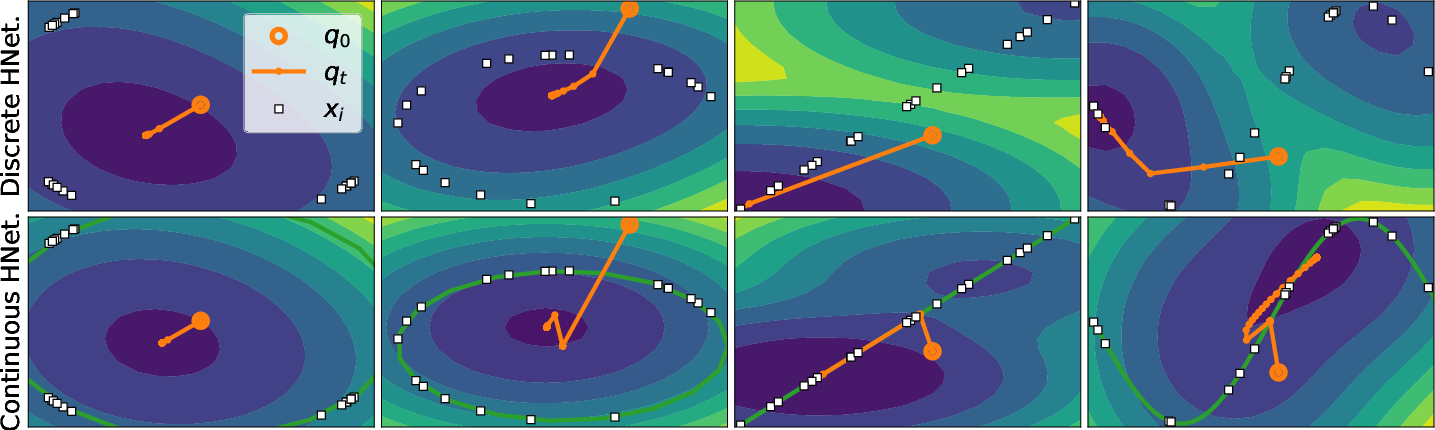
Figure 1: Optimization trajectories and energy contours for Hopfield networks with discrete (top) and continuous memories (bottom). Green illustrates the continuous function shaped by discrete memory points, while darker shades of blue indicate lower energy regions.

Implementation Details

The continuous-time memories are encoded using basis functions that reconstruct signals across a continuous domain, optimizing storage through multivariate ridge regression. The energy function is redefined as:

$$E(\bm{q}) = - \frac{1}{\beta}\log \int_{0}^1 \exp(\beta \bar{\bm{x}(t)}^\top \bm{q}) dt + \frac{1}{2} \|\bm{q}\|^2 + \text{const}.$$

The corresponding update rule modifies with each iteration based on a probability density function applied over the continuous reconstructed signal, leading to the Gibbs expectation update. Through numerical experiments, this new formulation shows improved retrieval performance with fewer memory bases, demonstrating its potential for efficient large-scale memory representation.

Experimental Evaluation

Experiments conducted on synthetic and video datasets showcased competitive performance of the continuous-time Hopfield networks compared to their discrete counterparts. Notably, the model demonstrated effective memory retrieval and representation across varying dimensions and contexts, maintaining stability and efficiency even with minimal basis function counts.

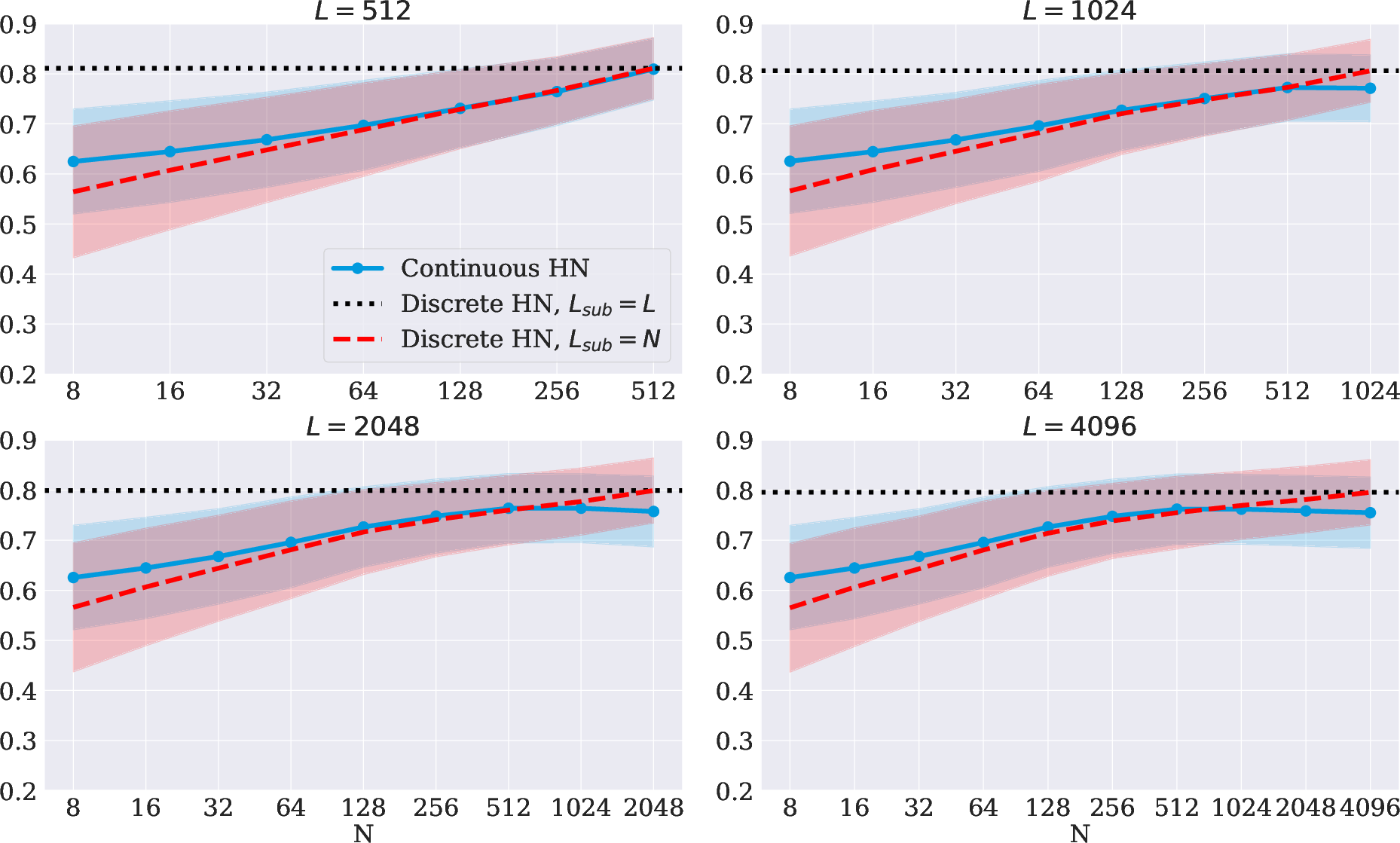
Figure 2: Video retrieval performance across different numbers of basis functions. Plotted are the cosine similarity means and standard deviations across videos.

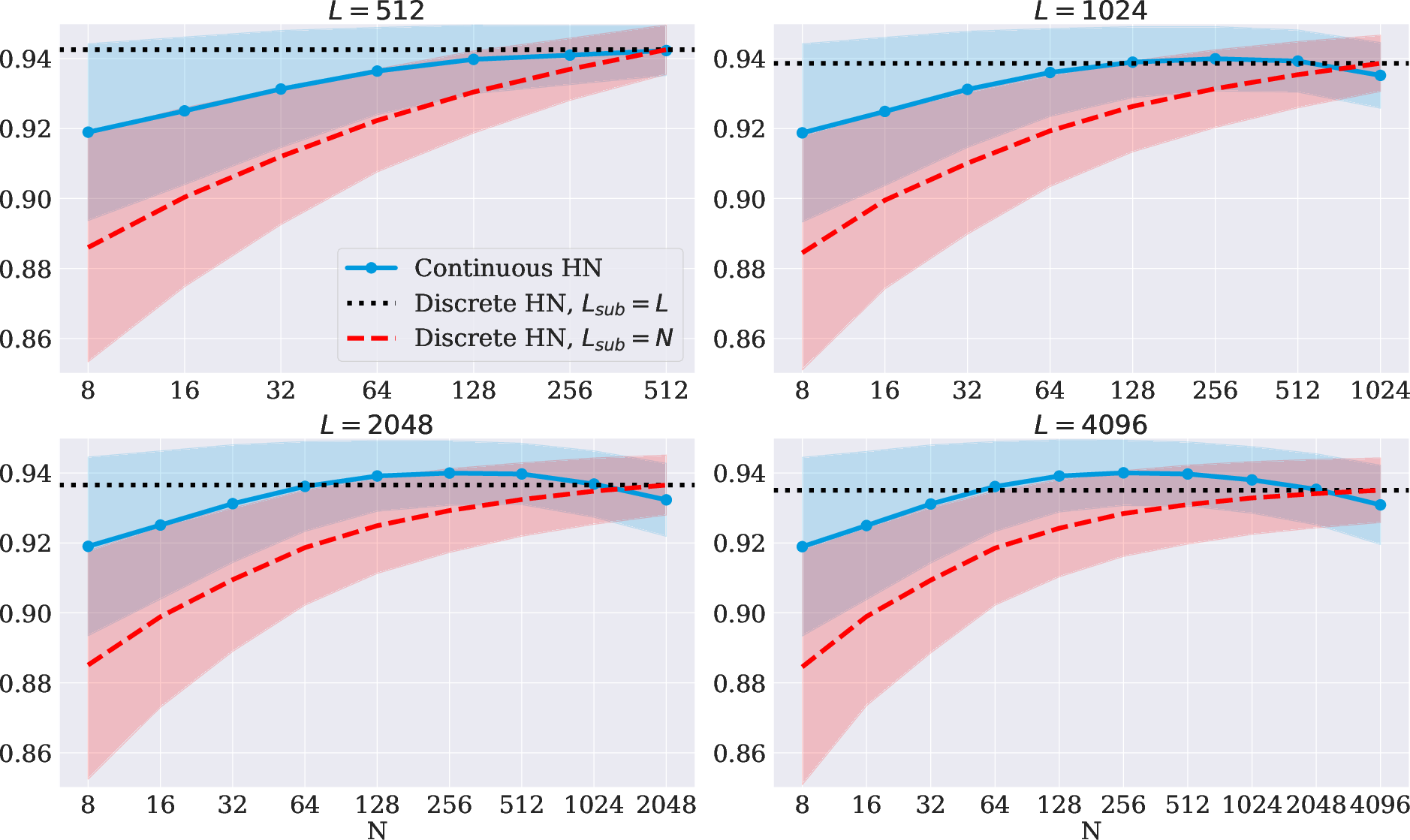
Figure 3: Video embedding retrieval performance across different numbers of basis functions. Plotted are the cosine similarity means and standard deviations across videos.

Conclusions

The continuous-time Hopfield network formulation presented in this research promotes advancements in memory-efficient architectures by embedding continuous attention mechanisms within modern Hopfield dynamics. While maintaining comparable performance to discrete memory systems, this approach suggests significant computational benefits for large-scale applications. Future work entails optimizing the allocation dynamics of basis functions, potentially replacing the ridge regression with adaptive models to achieve better expressiveness and capacity improvements. This ongoing exploration into continuous-memory systems reflects a compelling intersection of computational neuroscience and machine learning, demonstrating theoretical and practical implications for artificial intelligence research and applications.