Shapley Value Approximation Based on k-Additive Games (2502.04763v1)

Abstract: The Shapley value is the prevalent solution for fair division problems in which a payout is to be divided among multiple agents. By adopting a game-theoretic view, the idea of fair division and the Shapley value can also be used in machine learning to quantify the individual contribution of features or data points to the performance of a predictive model. Despite its popularity and axiomatic justification, the Shapley value suffers from a computational complexity that scales exponentially with the number of entities involved, and hence requires approximation methods for its reliable estimation. We propose SVA$k_{\text{ADD}}$, a novel approximation method that fits a $k$-additive surrogate game. By taking advantage of $k$-additivity, we are able to elicit the exact Shapley values of the surrogate game and then use these values as estimates for the original fair division problem. The efficacy of our method is evaluated empirically and compared to competing methods.

• The paper presents a novel algorithm (SVA‑k_ADD) that approximates Shapley values using k‑additive surrogate games to reduce computational complexity.
• It employs a weighted least squares approach with optimal coalition sampling to guarantee exact recovery for k=1,2,3 under full sampling.
• Empirical results demonstrate that SVA‑k_ADD outperforms or matches state‑of‑the‑art methods in feature attribution tasks across diverse datasets.

Shapley Value Approximation via k-Additive Games: Theory, Algorithms, and Empirical Analysis

Introduction and Motivation

The Shapley value is a canonical solution concept in cooperative game theory, uniquely satisfying axioms of fairness for distributing the value generated by a coalition among its members. Its adoption in machine learning, particularly for feature attribution and model explainability, has been extensive due to its axiomatic justification and interpretability. However, the exponential computational complexity of exact Shapley value calculation ($O(2^n)$ for $n$ players/features) renders it infeasible for practical use in high-dimensional settings, necessitating efficient approximation algorithms.

This paper introduces SVA$k_{\text{ADD}}$, a novel Shapley value approximation method leveraging the structure of $k$-additive games. By fitting a $k$-additive surrogate to sampled coalition values, the method enables polynomial-time estimation of Shapley values, with theoretical guarantees for exact recovery under full sampling and empirical evidence of competitive performance against state-of-the-art baselines.

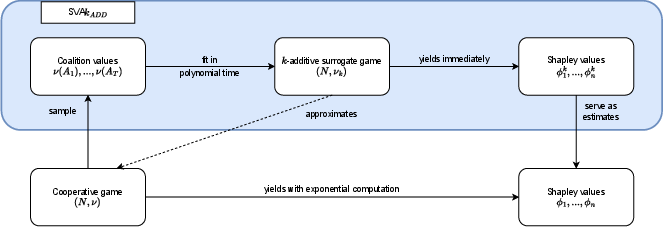
Figure 1: The SVA$k_{\text{ADD}}$ pipeline: sampled coalition values $\nu(A_1),\ldots,\nu(A_T)$ are used to fit a $k$-additive surrogate game $(N,\nu_k)$, from which Shapley values $\phi_1^k,\ldots,\phi_n^k$ are computed directly and serve as estimates for the original game.

Theoretical Foundations: k-Additivity and Shapley Interactions

A cooperative game $(N, \nu)$ is defined by a set of players $N$ and a value function $\nu: \mathcal{P}(N) \to \mathbb{R}$. The Shapley value for player $i$ is given by:

$$\phi_i = \sum_{A \subseteq N \setminus \{i\}} \frac{(n - |A| - 1)! |A|!}{n!} [\nu(A \cup \{i\}) - \nu(A)]$$

The concept of $k$-additivity restricts the game such that all interaction indices $I(S)$ for $|S| > k$ vanish. This reduces the number of parameters from $2^n$ to $O(n^k)$, enabling tractable surrogate modeling. The surrogate game $(N, \nu_k)$ is parameterized by interaction indices up to order $k$, and the Shapley value for each player is directly given by the singleton interaction $I^k(\{i\})$.

The paper proves that, with a specific choice of coalition sampling weights $w_A^* = \binom{n-2}{|A|-1}^{-1}$, the solution to the $k$-additive weighted least squares problem yields the exact Shapley values for $k=1,2,3$ when all coalitions are observed. This result holds regardless of the true game's additivity, establishing the theoretical soundness of the approach.

SVA$k_{\text{ADD}}$: Algorithmic Details

The SVA$k_{\text{ADD}}$ algorithm proceeds as follows:

1. Sampling: Draw $T$ coalitions (including $\emptyset$ and $N$) according to the derived optimal weights.
2. Surrogate Fitting: Solve a constrained weighted least squares problem to fit the $k$-additive surrogate $\nu_k$ to the sampled coalition values.
3. Shapley Value Extraction: Compute the Shapley values $\phi^k$ from the fitted surrogate, which serve as estimates for the original game.

The optimization problem is:

$$\min_{I^k} \sum_{A \in \mathcal{M} \setminus \{\emptyset, N\}} w_A \left( \nu(A) - \nu_k(A) \right)^2$$

subject to the efficiency constraint $$\nu(N) - \nu(\emptyset) = \nu_k(N) - \nu_k(\emptyset)$$. The problem is solved analytically or via standard linear algebra routines, as detailed in the appendix.

Empirical Evaluation: Approximation Quality and Trade-offs

The empirical analysis spans global, local, and unsupervised feature importance tasks across diverse datasets (Diabetes, Titanic, Wine, Adult, ImageNet, IMDB, Breast Cancer, Big Five, FIFA). The main evaluation metric is mean squared error (MSE) between estimated and true Shapley values, computed exhaustively for tractable $n$.

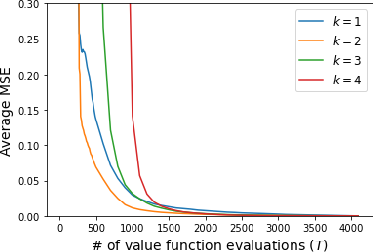
Figure 2: MSE of SVA$k_{\text{ADD}}$ for varying $k$ and sample budget $T$ across datasets; higher $k$ yields faster convergence but requires more samples for identifiability.

Key findings:

• Additivity Degree ($k$) Trade-off: Low $k$ (e.g., $k=1$) leads to slow convergence due to insufficient model flexibility. Increasing $k$ accelerates convergence but raises sample requirements. Empirically, $k=3$ offers a favorable balance for most datasets.
• Comparison to Baselines: SVA$k_{\text{ADD}}$ (with $k=3$) matches or outperforms stratified SVARM and KernelSHAP in most settings, especially for local attribution tasks. For very small sample budgets, stratified SVARM may be superior, but SVA$k_{\text{ADD}}$ overtakes as $T$ increases.

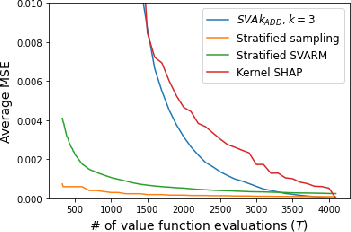
Figure 3: Comparative MSE of SVA$k_{\text{ADD}}$ and competing methods (Stratified SVARM, KernelSHAP, Permutation sampling) as a function of sample budget $T$.

• Domain Independence: The method is model-agnostic and applicable to any cooperative game, including unsupervised settings where the value function is based on total correlation.

Implementation Considerations

• Computational Complexity: For fixed $k$, the surrogate fitting scales polynomially in $n$ and linearly in the number of samples $T$. The main bottleneck is coalition value evaluation, especially when retraining models for each coalition.
• Sample Budget: The minimum required $T$ grows with $k$ and $n$ due to identifiability constraints. For $k=3$, $T = O(n^3)$ suffices.
• Deployment: SVA$k_{\text{ADD}}$ is suitable for settings where coalition evaluation is expensive and sample efficiency is critical. It is particularly advantageous when higher-order interactions are negligible or when interpretability of interaction effects is desired.

Limitations and Future Directions

• Scalability: While polynomial in $n$ for fixed $k$, the approach becomes impractical for large $n$ and high $k$ due to the combinatorial growth of interaction terms.
• Approximation Guarantees: No theoretical bounds are provided for the approximation error under partial sampling; empirical results suggest strong performance, but formal analysis remains open.
• Interaction Effects: The method estimates interaction indices up to order $k$, enabling analysis of feature redundancy and complementarity, which is valuable for feature engineering and scientific discovery.

Conclusion

SVA$k_{\text{ADD}}$ provides a theoretically justified and empirically validated approach for Shapley value approximation via $k$-additive surrogate games. It offers a flexible trade-off between model expressiveness and sample efficiency, competitive performance against leading baselines, and broad applicability across explanation tasks. Future work may extend theoretical analysis to arbitrary $k$, explore adaptive sampling strategies, and leverage estimated interaction indices for deeper interpretability.