Inverse Reinforcement Learning via Convex Optimization (2501.15957v2)

Abstract: We consider the inverse reinforcement learning (IRL) problem, where an unknown reward function of some Markov decision process is estimated based on observed expert demonstrations. In most existing approaches, IRL is formulated and solved as a nonconvex optimization problem, posing challenges in scenarios where robustness and reproducibility are critical. We discuss a convex formulation of the IRL problem (CIRL) initially proposed by Ng and Russel, and reformulate the problem such that the domain-specific language CVXPY can be applied directly to specify and solve the convex problem. We also extend the CIRL problem to scenarios where the expert policy is not given analytically but by trajectory as state-action pairs, which can be strongly inconsistent with optimality, by augmenting some of the constraints. Theoretical analysis and practical implementation for hyperparameter auto-selection are introduced. This note helps the users to easily apply CIRL for their problems, without background knowledge on convex optimization.

• The paper reformulates the IRL problem as a convex optimization task, ensuring global optimality in estimating reward functions.
• It leverages CVXPY and an ℓ1-penalty to enforce sparsity and balance objectives with an iterative bisection method for hyperparameter tuning.
• It demonstrates practical applicability in both static and nonstationary environments, enhancing reproducibility and reliability in dynamic systems.

Inverse Reinforcement Learning via Convex Optimization

Introduction

This paper focuses on addressing the challenges inherently tied to the nonconvex nature of traditional Inverse Reinforcement Learning (IRL) problem formulations. By leveraging a convex optimization approach, the authors aim to estimate an unknown reward function of a Markov Decision Process (MDP) more efficiently and reliably. The approach initially proposed by Ng and Russell is extended here to handle scenarios where expert policies are inferred from trajectories as state-action pairs, which are often inconsistent with optimal strategies.

Problem Formulation

IRL traditionally seeks to deduce the reward function underlying behaviors observed from expert demonstrations. Typically, these problems are posed as nonconvex optimization tasks, making them computationally intensive and less reliable in terms of convergence and reproducibility. This work reformulates the problem as a Convex Inverse Reinforcement Learning (CIRL) problem. The appeal of convex optimization lies in its guarantees of finding global optima, which is particularly crucial in fields like psychology and neuroscience, where reproducibility is critically important.

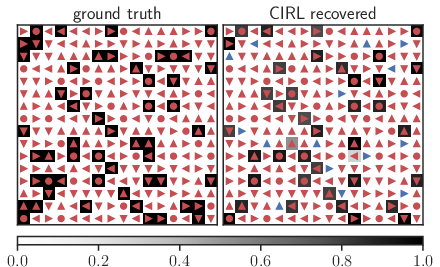
Figure 1: Left shows the $16 \times 16$ gridworld with optimal directions in red and the right displays the recovered reward and policy using CIRL, with discrepancies in blue.

The authors provide a comprehensive mathematical framework for their approach, using CVXPY, a Python-embedded modeling language for specifying and solving convex optimization problems. The reformulation also includes theoretical backing for hyperparameter auto-selection, aiding practical implementation without requiring profound knowledge of convex optimization.

Theoretical and Practical Insights

The reward function in CIRL is optimized to maximize the margin between the expert policy and all other possible policies. The solution set is truncated by imposing sparsity-inducing $\ell_1$-penalty terms, ensuring meaningful solutions over trivial ones. To solve the CIRL problem accurately, it is formulated in a regularized linear program epigraph form that can be efficiently handled by CVXPY.

The hyperparameter $\lambda$ plays a pivotal role in balancing the primary objective and sparsity term. The paper derives the critical value for $\lambda$, guaranteeing an optimal solution characterized by maximum sparsity, without degenerating to the trivial solution of a null reward function. Additionally, a practical iterative bisection method is suggested to fine-tune $\lambda$.

Application to Nonstationary Reward Functions

IRL instances with nonstationary reward distributions, where experts aim for dynamic subgoals, typically challenge traditional methodologies. The CIRL model adapts to such environments by relaxing some constraints to accommodate local optimality in subgoal-oriented tasks.

Figure 2: Greedy snake environment illustrating expert's trajectory and respective reward distributions.

An example involves the greedy snake environment with a dynamic configuration where experts exhibit trajectories with changing targets. By employing partitioning strategies and solving the relaxed CIRL problem sections, it effectively estimates the variable reward functions which facilitate the snake's segmented trajectory.

Implementation and Experimentation

Two primary examples elaborate the CIRL's practical applicability. The gridworld test, a static environment, demonstrated a high similarity measure with authentic reward distribution and policy prediction efficacy, achieved in a fraction of the time compared to other IRL algorithms. The greedy snake scenario depicted the adaptability in nonstationary contexts, showcasing the accurate identification of shifting reward locations and subsequent optimization of segmented trajectories.

Conclusion

This paper significantly extends the CIRL problem's formulation by providing generalized solutions for environments where expert behaviors are non-optimal and incompletely described. The mathematical rigor, combined with an adaptable computational methodology via CVXPY, empowers practitioners to employ IRL efficiently in complex dynamic systems. The practical implications extend to automated driving and cognitive behavioral modeling, where reward estimation reliability and reproducibility are indispensable.

The promise of enhanced interpretability and reproducibility in IRL underscores the potential improvements in robotic autonomy and human behavior modeling, emphasizing the framework's relevance in both theoretical exploration and actionable applications.