Chain-of-Reasoning: Towards Unified Mathematical Reasoning in Large Language Models via a Multi-Paradigm Perspective (2501.11110v4)

Abstract: LLMs have made notable progress in mathematical reasoning, yet often rely on single-paradigm reasoning, limiting their effectiveness across diverse tasks. We introduce Chain-of-Reasoning (CoR), a novel unified framework integrating multiple reasoning paradigms--Natural Language Reasoning (NLR), Algorithmic Reasoning (AR), and Symbolic Reasoning (SR)--to enable synergistic collaboration. CoR generates multiple potential answers via different reasoning paradigms and synthesizes them into a coherent final solution. We propose a Progressive Paradigm Training (PPT) strategy for models to progressively master these paradigms, leading to CoR-Math-7B. Experimental results demonstrate that CoR-Math-7B significantly outperforms current SOTA models, achieving up to a 41.0% absolute improvement over GPT-4o in theorem proving and a 15.0% improvement over RL-based methods on the MATH benchmark in arithmetic tasks. These results show the enhanced mathematical comprehension ability of our model, enabling zero-shot generalization across tasks.

• The paper proposes a multi-paradigm Chain-of-Reasoning framework combining natural language, algorithmic, and symbolic reasoning to improve mathematical problem-solving in LLMs.
• The methodology employs Progressive Paradigm Training and Sequential Multi-Paradigm Sampling to iteratively enhance performance across benchmark tasks.
• The paper reports up to a 41% improvement in theorem proving and a 7.9% gain in arithmetic efficiency over state-of-the-art models.

Chain-of-Reasoning: Towards Unified Mathematical Reasoning in LLMs via a Multi-Paradigm Perspective

Introduction

The research explores the limitations of traditional LLMs in addressing mathematical reasoning across diverse tasks, which has historically been constrained by reliance on single-paradigm reasoning. By introducing the Chain-of-Reasoning (CoR) framework, the paper aims to unify multiple reasoning paradigms—Natural Language Reasoning (NLR), Algorithmic Reasoning (AR), and Symbolic Reasoning (SR)—to enable LLMs to engage in more synergistic and comprehensive problem-solving. This approach is encapsulated in the developed model, CoR-Math-7B, which demonstrates significant improvements over current models in diverse mathematical reasoning benchmarks.

Methodology

The CoR framework operates by synthesizing multiple reasoning paradigms to derive coherent solutions to mathematical problems. This involves initializing a problem statement within the NLR paradigm, progressing through the AR paradigm for precise calculations, and concluding with SR for formal proof validation. This multi-paradigm interaction allows for reasoning depth to be modulated according to task requirements, thereby improving adaptability and cross-task generalization.

To train models effectively within this framework, the authors propose the Progressive Paradigm Training (PPT) strategy, which incrementally introduces diverse paradigms to enhance the model's reasoning capabilities. The training process involves constructing the Multi-Paradigm Math (MPM) dataset, which incorporates tasks necessitating different reasoning paradigms combined into coherent reasoning paths.

The inference process of CoR-Math-7B supports zero-shot task adaptation, utilizing Sequential Multi-Paradigm Sampling (SMPS) to explore diverse solutions across paradigms. This involves a step-by-step reasoning approach, followed by the application of symbolic proof systems where necessary, ensuring formal correctness of solutions.

Evaluation and Results

The effectiveness of the CoR framework is substantiated by extensive experiments on established mathematical reasoning benchmarks, including MATH, GSM8k, and MiniF2F. CoR-Math-7B exhibits superior performance, achieving up to a 41.0% improvement in theorem proving over GPT-4, while maintaining efficiency in arithmetic tasks with a 7.9% improvement over reinforcement learning methods.

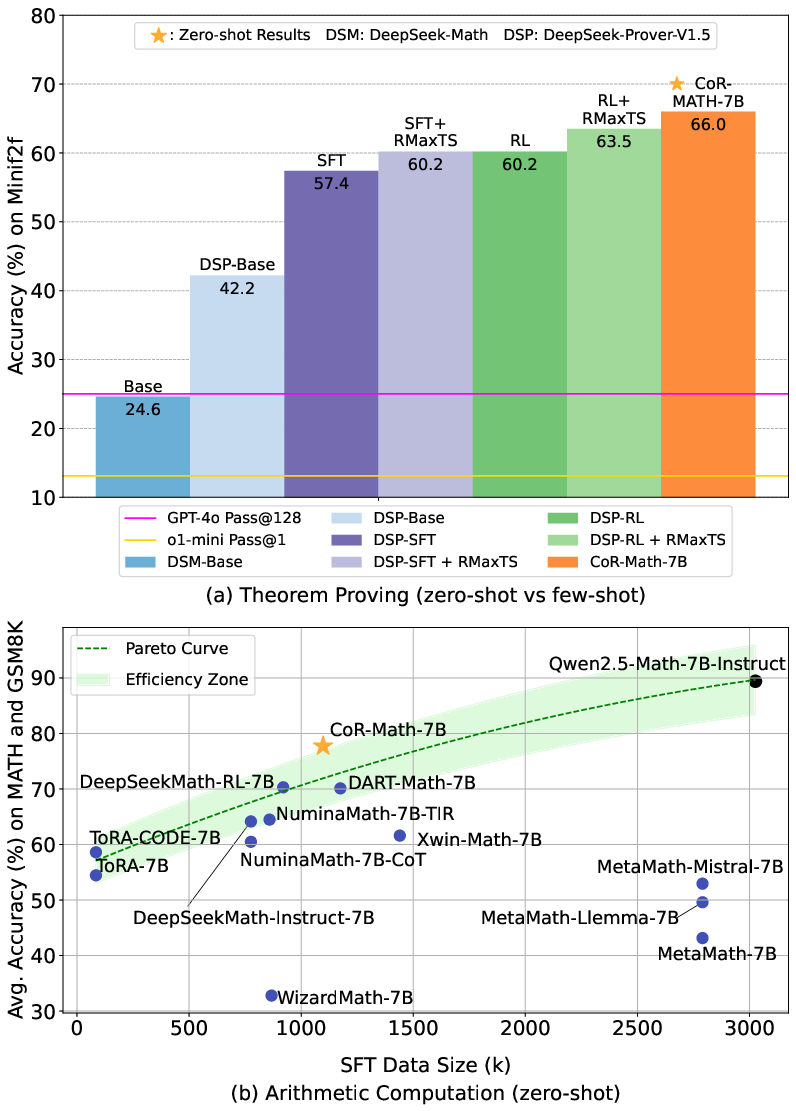
Figure 1: A comprehensive comparative analysis of CoR-Math-7B and baseline models across mathematical tasks. (a) shows the effectiveness of CoR-Math-7B (zero-shot) in theorem proving tasks. (b) shows a resource-efficiency analysis for arithmetic computation tasks, where CoR-Math-7B achieves optimal resource efficiency and near-optimal zero-shot performance.

The results indicate that CoR-Math-7B efficiently uses computational resources while surpassing the performance of baseline models. This aligns with the theoretical expectation that incorporating diverse reasoning modalities can enhance problem-solving capabilities beyond what is achievable with single-paradigm reasoning.

Impact of Training Strategies

The implementation of the PPT strategy reveals substantial improvements in model performance across different reasoning tasks, highlighting the advantage of multi-stage training approaches. Empirical results suggest that models trained through PPT exhibit enhanced adaptability and higher accuracy in handling complex problem-solving scenarios.

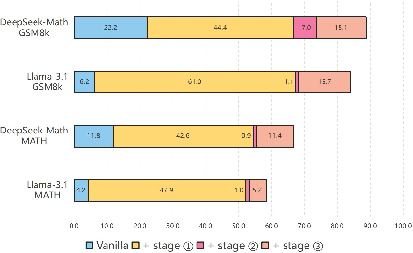
Figure 2: An evaluation of the effectiveness of the PPT strategy. We present the zero-shot Pass@1 results on the MATH and GSM8k benchmarks across three cumulative stages of the PPT strategy. The results highlight the PPT strategy's cumulative effectiveness, showing increased performance with each progressive stage.

Implications and Future Work

The introduction of multi-paradigm reasoning frameworks like CoR prompts a reevaluation of reasoning strategies in AI research. By emphasizing a modular and integrative approach to problem-solving, this research paves the way for developing LLMs with enhanced capabilities in diverse application areas. Future work could explore scaling such frameworks across larger datasets and more diverse problem types, potentially integrating additional paradigms like graph-based or visual reasoning to further enhance logical inference and decision-making in AI systems.

Conclusion

The Chain-of-Reasoning framework presents a novel approach to unifying mathematical reasoning paradigms in LLMs, demonstrating substantial improvements in performance and resource efficiency. This work represents a critical step towards developing more versatile AI systems capable of addressing complex reasoning tasks across various domains, marking a shift from traditional single-paradigm to holistic multi-paradigm reasoning strategies in AI research.