Riding Wavelets: A Method to Discover New Classes of Price Jumps (2404.16467v1)

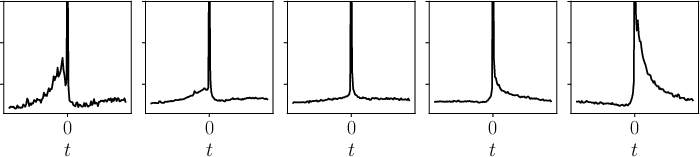
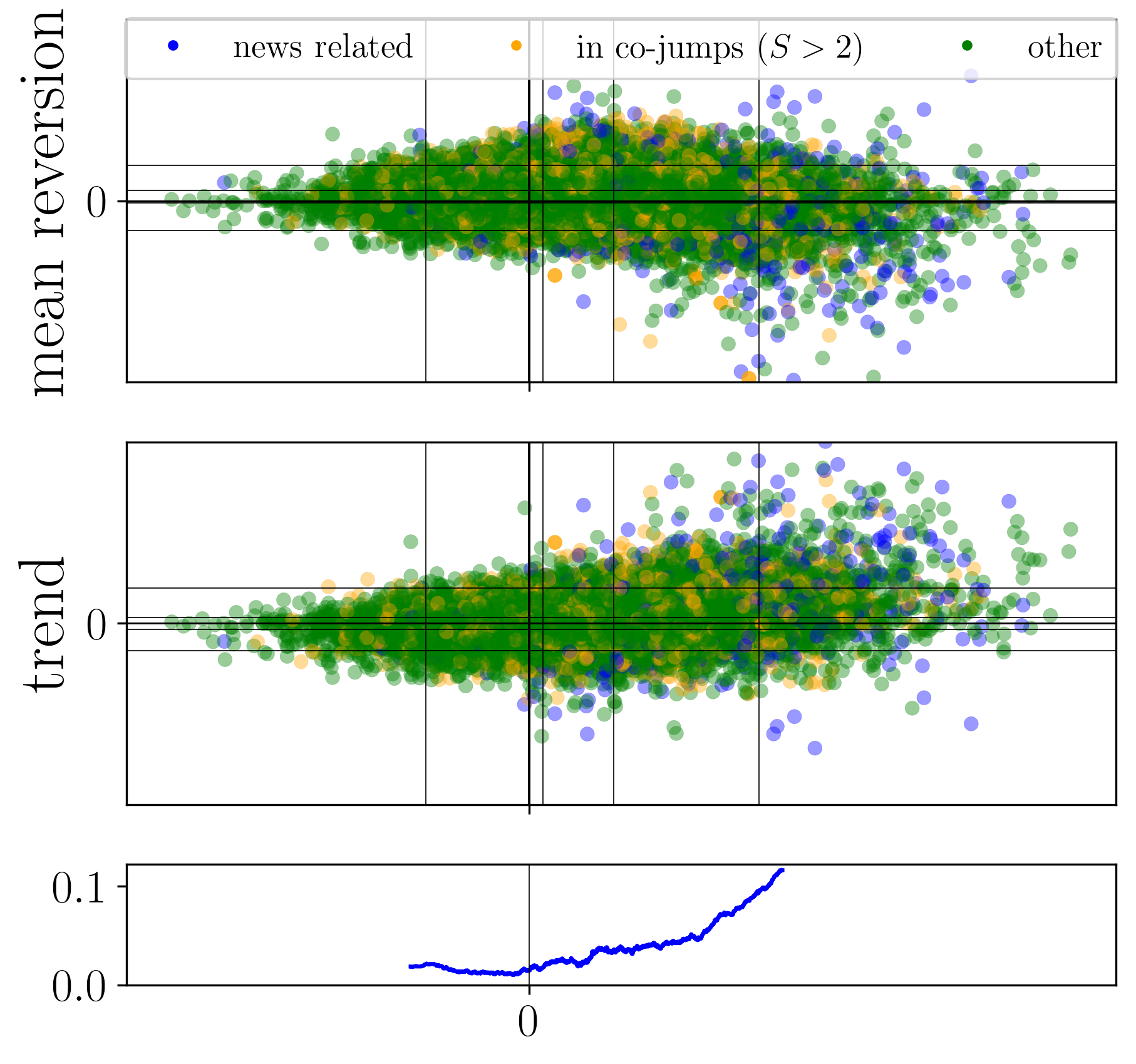
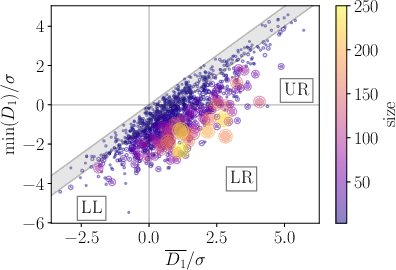
Abstract: Cascades of events and extreme occurrences have garnered significant attention across diverse domains such as financial markets, seismology, and social physics. Such events can stem either from the internal dynamics inherent to the system (endogenous), or from external shocks (exogenous). The possibility of separating these two classes of events has critical implications for professionals in those fields. We introduce an unsupervised framework leveraging a representation of jump time-series based on wavelet coefficients and apply it to stock price jumps. In line with previous work, we recover the fact that the time-asymmetry of volatility is a major feature. Mean-reversion and trend are found to be two additional key features, allowing us to identify new classes of jumps. Furthermore, thanks to our wavelet-based representation, we investigate the reflexive properties of co-jumps, which occur when multiple stocks experience price jumps within the same minute. We argue that a significant fraction of co-jumps results from an endogenous contagion mechanism.

• The paper introduces a novel unsupervised framework using wavelet scattering coefficients to classify price jumps by capturing time-asymmetry, mean-reversion, and trend.
• It employs PCA on high-frequency US stock data to distinguish between anticipatory, endogenous, and exogenous jumps with clear statistical separation.
• The study highlights endogenous contagion in co-jumps, offering practical insights for risk management and market stability.

Riding Wavelets: A Method to Discover New Classes of Price Jumps

This paper introduces an unsupervised framework for classifying financial price jumps using wavelet-based representations and applies it to a dataset of US stock prices. The method identifies key features, including volatility asymmetry, mean-reversion, and trend, to distinguish different classes of jumps, and explores the reflexive properties of co-jumps to determine the extent of endogenous contagion mechanisms.

Methodology and Data

The research leverages a dataset of price jumps detected using a jump-score estimator on 1-minute returns time-series. The jump-aligned version of the time-series, $\nosx(t)$, is analyzed within a 2-hour window centered around the jump. The dataset comprises 37,452 jumps from 301 US stocks between January 2015 and December 2022, after filtering for major market shocks and FED announcements. Co-jumps are defined as simultaneous jumps of multiple stocks within the same minute.

The core of the methodology involves embedding each jump time-series into a low-dimensional space using wavelet scattering coefficients. These coefficients, derived from wavelet transforms of the time-series and its volatility, capture time-asymmetry and other relevant features at multiple scales. PCA is then applied to identify the principal components that best discriminate between different classes of jumps.

Key Findings on Univariate Jump Classification

The PCA reveals three salient features: time-asymmetry of volatility (reflexivity), mean-reversion, and trend. The first principal component, $D_1$, is a linear combination of wavelet coefficients that characterizes the time-asymmetry of the volatility profile. This direction separates jumps into three types: anticipatory, endogenous, and exogenous (Figure 1).

Figure 1: Average absolute profiles $|x(t)|$ of jumps along direction $D_1$ (sliced into five bins, delimited by quantiles 0.1, 0.25, 0.35, 0.9). From left to right: anticipatory jumps, endogenous jumps and exogenous jumps.

Anticipatory jumps exhibit dominant activity before the shock, endogenous jumps show symmetric activity around the shock, and exogenous jumps display dominant activity after the shock. It is found that approximately 50% of the sample exhibits positive asymmetry, suggesting exogenous jumps are common.

The second key feature identified is mean-reversion, captured by coefficients $\text{Im}\,W_{j_1}\nosx(0)$ for fine scales. A handcrafted filter, $\psi_\text{MR}$, is designed to capture short-time mean-reversion (Figure 2), and a corresponding direction $\widetilde{D}_2$ is defined.

Figure 2: $\psi_\text{MR}$.

The third feature is trend, which describes post-jump returns continuing in the same direction as pre-jump returns. A trend filter, $\psi_\text{TR}$, is designed to capture this behavior (Figure 2), defining a trend score $\widetilde{D}_3$. Jumps are then classified as either trend-aligned or trend-anti-aligned based on the sign of $\widetilde{D}_3$.

The dataset of jumps can be visualized in two 2D projections (Figure 3), one using $D_1$ and $\widetilde{D}_2$ and the other using $D_1$ and $\widetilde{D}_3$.

Figure 3: \underline{Top graph}.

These projections allow for an embedding of each jump according to its self-reflexive nature, mean-reversion character, or trend character.

Analysis of Co-jumps

Co-jumps are analyzed to investigate the extent of endogenous dynamics versus exogenous shocks. The size distribution of co-jumps follows a power-law, $S^{-\tau}$, with $\tau \approx 1$, suggesting a contagion mechanism.

The individual reflexivity scores, $D_1$, are aggregated for each co-jump using the average ($\overline{D_1}$), maximum, and minimum values. By plotting the minimum value of $D_1$ against the average value (Figure 4), co-jumps can be classified as endogenous, exogenous, or a combination.

Figure 4: Minimum value of reflexivity score D_1 over all jumps of a given co-jump as a function of the average value $\overline{D_1}$

.

It is observed that many large co-jumps are driven by endogenous dynamics, propagating across stocks rather than stemming from external news.

The correlation of jump time-series within a co-jump is also examined. While larger co-jumps tend to have more correlated constituents, a significant number of large co-jumps exhibit weak correlations, further supporting the endogenous contagion hypothesis.

Implications and Future Directions

This unsupervised approach, based on wavelet scattering coefficients, provides a method for classifying price jumps and co-jumps. The identification of time-asymmetry, mean-reversion, and trend as key features allows for a more nuanced understanding of market dynamics and the origins of extreme events. The finding that a significant proportion of co-jumps are driven by endogenous dynamics has implications for risk management and market stability. Future work should focus on higher frequency data to dissect the contagion mechanism and explore the relationship between market fragility and co-jump occurrences. The wavelet scattering embedding can be applied to other fields beyond finance.

Conclusion

The use of wavelet scattering coefficients offers a robust and versatile framework for classifying price jumps and co-jumps. The research highlights the importance of considering endogenous dynamics in financial markets and provides insights into the mechanisms driving market instability.