Correlated phases and topological phase transition in twisted bilayer graphene at one quantum of magnetic flux (2402.00884v2)

Abstract: When the perpendicular magnetic flux per unit cell in a crystal is equal to the quantum of magnetic flux, $Φ_0=h/e$, we enter the 'Hofstadter regime'. The large unit cell of moiré materials like magic-angle twisted bilayer graphene (MATBG) allows the experimental study of this regime at feasible values of the field around $20$ to $30$ T. In this work, we report numerical analysis of a tight-binding model for MATBG at one quantum of external magnetic flux, including the long-range Coulomb and on-site Hubbard interaction. We study the correlated states for dopings of $-2,0$ and $2$ electrons per unit cell at the mean-field level. We find competing insulators with Chern numbers $2$ and $0$ at positive doping, the stability of which is determined by the dielectric screening, which opens up the possibility of observing a topological phase transition in this system.

• The paper demonstrates that applying one quantum of magnetic flux to MATBG triggers competing insulating states with distinct Chern numbers using self-consistent Hartree-Fock simulations.
• It utilizes a detailed tight-binding model with Peierls' substitution to incorporate Zeeman splitting and long-range Coulomb interactions, highlighting symmetry reductions.
• The numerical analysis clarifies the influence of dielectric screening and electron doping (ν = 0 and ±2) in driving tunable topological phase transitions.

Correlated Phases and Topological Phase Transition in Twisted Bilayer Graphene at One Quantum of Magnetic Flux

Introduction

This paper investigates the electronic properties of magic-angle twisted bilayer graphene (MATBG) under one quantum of magnetic flux. MATBG is known for hosting a variety of exotic phases, which include superconductors and Fractional Chern insulators. The analysis focuses on the Hofstadter regime where a tight-binding model, incorporating both long-range Coulomb and on-site Hubbard interactions, is employed to scrutinize the correlated states at various electron dopings per unit cell. Remarkably, the paper observes competing insulators with varying Chern numbers, thus opening the possibility of a topological phase transition.

Theoretical Model

The model considers two rotated graphene layers with meticulously defined interlayer geometry and hopping parameters aligned with the Slater-Koster scheme.

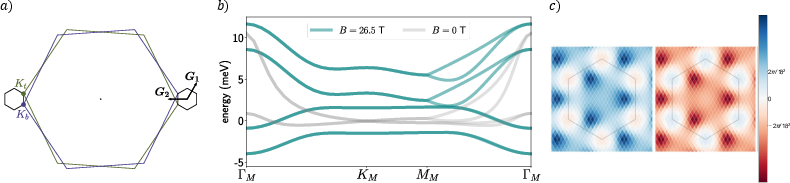
Figure 1: The Brillouin zone of the rotated top and bottom layers.

Key elements of the Hamiltonian include terms for Zeeman splitting and long-range electron-electron interactions. The hopping parameters are adjusted for magnetic field effects using Peierls' substitution. Symmetry operations under the magnetic field, including $C_{3z}$ and $C_{2z}$, are explained, highlighting how these affect the momentum space and symmetry preservation under flux conditions.

Numerical Analysis

The paper utilizes self-consistent Hartree-Fock (HF) simulations focusing on the Hofstadter spectrum at significant magnetic fields, around $26.5$ T. The implementation involves projecting the relevant interactions onto the flat bands, allowing for the evaluation of the leading order parameters.

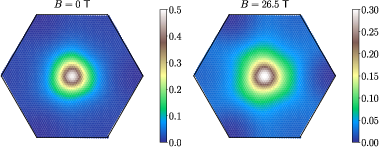
Figure 2: Density distribution of the flat bands for $0$ and $26.5$ T.

The $U(4)$ symmetry of the Coulomb interaction, almost preserved by valley and spin degrees of freedom, is scrutinized under symmetry breaking terms, showing that the total symmetry is reduced in applied fields and interactions. The symmetry breaking results in competitive valley polarized and intervalley coherent orders.

Results

Doping $\nu = \pm 2$:

The paper discovers that the system is spin-polarized, with strong indications of Chern numbers aligning with Quantum Hall states. The Hartree-Fock method reveals that Chern insulators appear robustly across the parameter space.

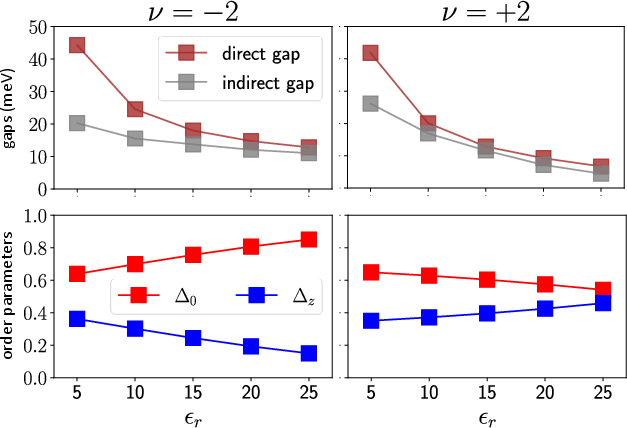
Figure 3: Gaps and order parameters for $\boldsymbol{\nu=\pm 2$}, showcasing dominant order parameters and associated many-body gaps.

Charge Neutrality ($\nu = 0$):

The spin-polarized (sp) state and an intervalley coherent (ivc) state compete, depending on interaction strengths and screening. Phase boundaries are clarified using various order parameters.

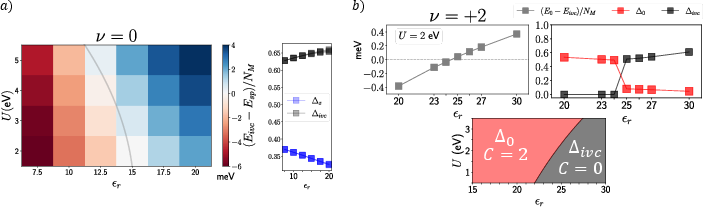
Figure 4: Competing states at charge neutrality, illustrating energy differences and phase transitions.

Topological Phase Transitions

At $\nu = +2$, a phase transition is identified, influenced significantly by dielectric screening. The transition manifests from a Quantum Hall regime to an intervalley coherent regime, marking a shift in the topological order.

Discussion

The findings align with and expand upon previously observed phenomena in experimental settings, such as those of Efetov et al. Experimental evidence reflects the robustness of the observed insulators, confirming their potential applicability in electronic devices leveraging topological properties.

Figure 5: Kinetic, Hubbard, and Coulomb energy evaluations during symmetry-breaking transformations.

Conclusion

The paper reinforces MATBG as a fertile ground for realizing tunable topological states under high magnetic fields. The numerical experiments suggest possible experimental realizations via dielectric or structural manipulation, which could transition the phase between Chern and trivial insulators, offering insights into novel electronic phase manipulation techniques.

This detailed analysis of MATBG at one magnetic flux quantum offers a new perspective into the tunable topological phases aided by advanced simulation techniques, adding to the growing body of knowledge on quantum materials and their potential high-impact applications.