Magnetically Induced Schrödinger Cat States: The Shadow of a Quantum Space (2309.16895v2)

Abstract: Schr\"odinger cat states, which are superpositions of macroscopically distinct states, are potentially critical resources for upcoming quantum information technologies. In this paper, we introduce a scheme to generate entangled Schr\"odinger cat states in a non-relativistic electric dipole system situated on a two-dimensional plane, along with an external potential and a uniform strong magnetic field perpendicular to the plane. Additionally, our findings demonstrate that this setup can lead to the phenomenon of collapse and revival of entanglement for a specific range of our model parameters

• The paper introduces a novel method to generate entangled Schrödinger cat states using a two-dimensional noncommutative system influenced by strong magnetic fields.
• It employs a hybrid model combining harmonic and impurity potentials to map dynamics between noncommutative and commutative frameworks, revealing collapse and revival of entanglement.
• Findings suggest practical implementations in semiconductor systems for scalable quantum computing and enhanced quantum error correction.

Magnetically Induced Schrödinger Cat States: The Shadow of a Quantum Space

This paper presents a novel approach for generating entangled Schrödinger cat states within a non-relativistic electric dipole system influenced by external magnetic fields. These states manifest from superpositions of macroscopically distinguishable states and hold potential as resources in quantum information technologies. The proposed scheme employs a two-dimensional setup with an external potential and mechanical constraints, exploring the emergence of non-commutative quantum states under strong magnetic field conditions.

Introduction to Schrödinger Cat States

Schrödinger cat states, or superpositions of macroscopically distinct quantum states, present insightful contributions to quantum mechanics' foundational debates, particularly in the context of wave function collapse. Beyond theoretical intrigue, these states bear practical significance in quantum technologies, including applications in metrology, quantum encryption, and error correction protocols. Challenges persist in their detection due to interference decay, yet experimental realizations span non-linear optics, superconductive cavities, and quantum dot systems.

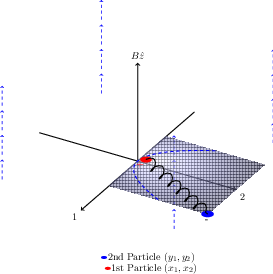
Figure 1: A schematic illustrating a magnetic field aligned along the $z$-axis, with oppositely charged particles connected by an interaction.

System Model and Non-Commutative Dynamics

The system under paper consists of two oppositely charged particles constrained to a plane orthogonal to a uniform magnetic field. Interactions are modeled both by a harmonic potential between the particles and with an impurity potential affecting one charge. Under ultra-strong magnetic conditions, kinetic energy contributions become negligible, confining dynamics to a non-commutative phase space inherently defined by the magnetic length. Here, the relational dynamics between canonical spatial variables and symplectic structures emerge distinctly (Figure 2).

Figure 2: Time evolution of the Purity function demonstrating variations in entanglement as a function of wavepacket width and external parameters.

Quantum Dynamics and Schrödinger Cat State Generation

Quantum extensions of the classical model translate into a non-trivial commutation structure, characterized by non-canonical Heisenberg algebras. The paper details how these non-commutative frameworks can naturally generate Schrödinger cat states via transitions facilitated by the plane's dynamics. When mapping between non-commutative and commutative frameworks, the system's ground state transforms into entangled superpositions, akin to cat states (Equation 33). Key parameters influencing state behavior include harmonic potential constants and alignment with magnetic constraints.

Entanglement Collapse and Revival in Schrödinger Cat States

The purity function serves as a quantifier for entanglement within generated Schrödinger cat states, revealing dependencies on both magnetic length and wavepacket characteristics. Increased values of non-commutative parameters capture heightened entanglement, while alterations to potential interactions lead to entanglement dynamics exhibiting collapse and revival phenomena. These findings align with predictions from modified Jaynes-Cummings models and offer insights into manipulating quantum coherence within composite bosonic systems.

Experimental Realization and Implications

Practical implementations are suggested in semiconductor layers where excitonic dipoles can emulate the described model. Specifically, systems with direct band-gap properties hold promise for realizing the required mass-symmetries and band alignments needed for effective reproductions of the theoretical model (Figure 3). Through controlled external field applications, entangled states possess utility not only in foundational compassions of quantum mechanics but also in scalable quantum computing applications, such as error correction via cat states.

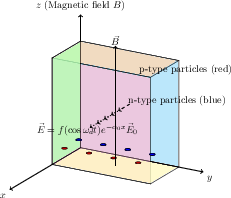
Figure 3: A 3D representation of a semiconductor layer with varied p-type and n-type particles, highlighting relevant field orientations and interactions.

Conclusion

The paper effectively demonstrates an approach to derive Schrödinger cat states in a quantum non-commutative space, with high applicability in technological paradigms where coherent quantum states are critical. The paper's implications outline novel pathways for entangled state generation in complex systems, potentially fuelling advancements in quantum information processing where these states might serve as computational qubits. Future work could extend examinations to include systems with Berry curvature influences or explore additional semiconductor materials conducive to such quantum behaviors.