Entanglement of Magnetically Levitated Massive Schrödinger Cat States by Induced Dipole Interaction (2304.14638v1)

Abstract: Quantum entanglement provides a novel way to test short-distance quantum physics in a non-relativistic regime. We provide entanglement-based protocols to potentially test the magnetically induced dipole-dipole interaction and the Casimir-Polder potential between the two nano-crystals kept in a Schrodinger Cat state. Our scheme is based on the Stern-Gerlach (SG) apparatus, where we can witness the entanglement mediated by these interactions for the nano-crystal mass m~10^-19 kg with a spatial superposition size of order 0.1 micron in a trap relying on diamagnetic levitation. We show that it is possible to close the SG interferometer in position and momentum with a modest gradient in the magnetic field.

• The paper demonstrates that magnetically levitated nano-crystals can achieve entanglement via induced dipole-dipole and Casimir-Polder interactions using a Stern-Gerlach interferometer.
• The paper reveals that a separation above 6 μm significantly enhances the entanglement phase, as validated by detailed simulations under low decoherence conditions.
• The paper outlines a framework to probe quantum gravity by leveraging controlled electromagnetic interactions to generate and measure macroscopic superposition states.

Entanglement of Magnetically Levitated Massive Schrödinger Cat States

Introduction

This paper investigates the use of quantum entanglement to explore short-range interactions within the quantum mechanics domain, specifically employing magnetically levitated Schrödinger cat states to probe interactions such as the dipole-dipole interaction and Casimir-Polder potential. These interactions are studied in the context of nano-crystals held in a spatial superposition using a Stern-Gerlach (SG) setup. This apparatus allows for potential investigations into quantum gravity by leveraging electromagnetic interactions as a baseline for quantum entanglement demonstrations.

Experimental Methodology

The research utilizes a Stern-Gerlach interferometer designed to generate and maintain spatial superpositions of massive nano-crystals, with masses approximately $10^{-19}$ kg. The SG apparatus creates a superposition through a magnetic field gradient, separating quantum states based on spin and enabling the interrogation of entanglement properties. The experimental setup involves the precise arrangement of magnetic traps and the application of pulsed magnetic fields to modulate spin states.

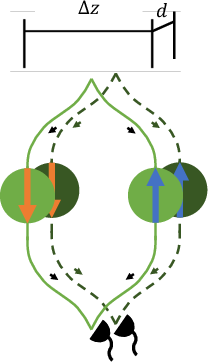
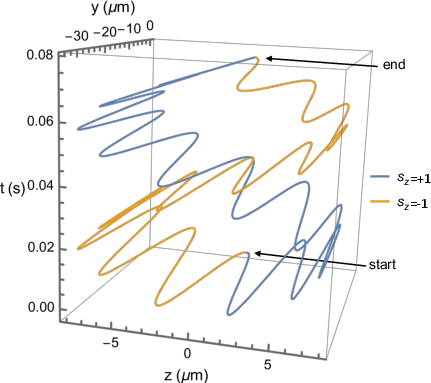
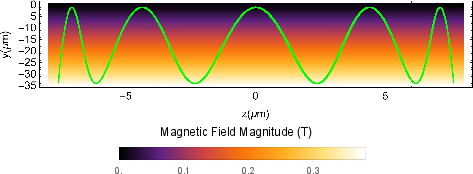
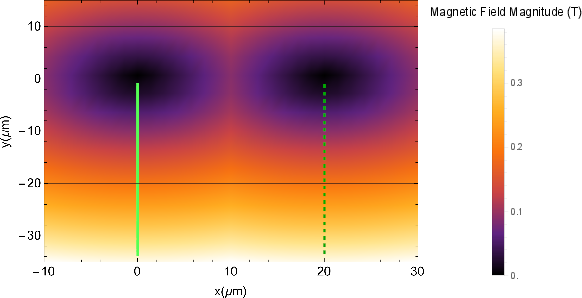
Figure 1: Simplified interferometer arrangement depicting the spatial configuration for inducing dipole interaction-mediated entanglement.

Quantum Interactions and Entanglement

The central focus of the paper is the entanglement arising from two primary electromagnetic interactions—Casimir-Polder and induced dipole-dipole interactions. The former arises due to virtual photons, while the latter is a result of external magnetic fields interacting with induced dipoles in the nano-crystals. The paper outlines how entangled states emerge when these interactions dominate at small separations (on the order of microns).

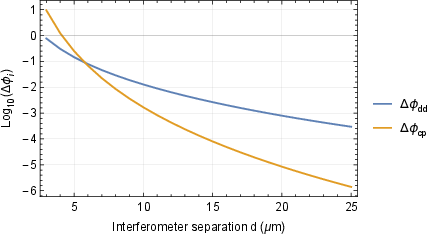
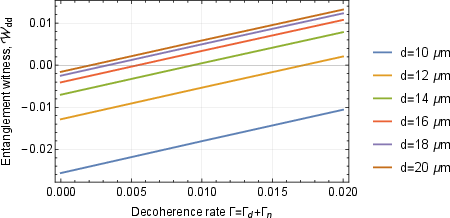
Figure 2: Entanglement phase comparison for different interaction sources.

The entanglement phase, a critical parameter, is indicative of the level of quantum interaction between particle states. This phase is influenced significantly by interaction distances and the strength of the magnetic field, as depicted by the experimental data and simulations.

Results and Analysis

The analysis reveals a dominant influence of the induced dipole-dipole interaction under specified conditions, particularly when the separation exceeds 6 μm. This interaction effect is discerned through comprehensive simulations and is characterized by a strong entanglement witness value under low decoherence conditions.

Figure 3: Example interferometer trajectory superimposed on the potential energy due to gravitational and magnetic influences.

Practical Implications and Future Directions

The research paves the way for enhanced understanding and utilization of quantum interactive forces in macroscopic superposition states. These insights are pivotal for designing experiments to probe quantum gravity effects, offering a methodological framework for implementing quantum tests at a laboratory scale. The paper underscores the need for further advancements in the control and measurement of quantum states to fully leverage the potential of these interactions in experimental physics.

Conclusion

The research elucidates critical approaches to harnessing quantum entanglement through electromagnetic interactions within interferometry setups. By isolating and controlling factors such as dipole-dipole interaction and superposition coherence, the framework sets the stage for advanced experimentation in quantum mechanics and potentially, quantum gravity. The evolved understanding reflects a step towards practical implementations of quantum systems in experimental physics, emphasizing the intricate dynamics of quantum fields and their potential applications.

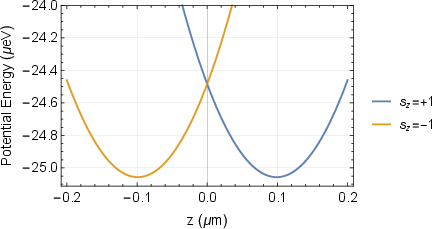
Figure 4: Potential energy distribution during pulsed magnetic field gradient for the spin states.