Quantifying Extrinsic Curvature in Neural Manifolds (2212.10414v3)

Abstract: The neural manifold hypothesis postulates that the activity of a neural population forms a low-dimensional manifold whose structure reflects that of the encoded task variables. In this work, we combine topological deep generative models and extrinsic Riemannian geometry to introduce a novel approach for studying the structure of neural manifolds. This approach (i) computes an explicit parameterization of the manifolds and (ii) estimates their local extrinsic curvature--hence quantifying their shape within the neural state space. Importantly, we prove that our methodology is invariant with respect to transformations that do not bear meaningful neuroscience information, such as permutation of the order in which neurons are recorded. We show empirically that we correctly estimate the geometry of synthetic manifolds generated from smooth deformations of circles, spheres, and tori, using realistic noise levels. We additionally validate our methodology on simulated and real neural data, and show that we recover geometric structure known to exist in hippocampal place cells. We expect this approach to open new avenues of inquiry into geometric neural correlates of perception and behavior.

• The paper introduces a framework that uses topological data analysis and variational autoencoders to quantify extrinsic curvature in neural manifolds.
• It applies differential geometric techniques with Riemannian metrics to accurately estimate curvature profiles, demonstrating minimal errors on synthetic and real neural data.
• The approach provides new insights into neural coding and offers potential improvements for neural network design and cognitive map analysis.

Quantifying Extrinsic Curvature in Neural Manifolds

The paper "Quantifying Extrinsic Curvature in Neural Manifolds" introduces a framework for understanding the geometric structures of neural manifolds using topological deep generative models and extrinsic Riemannian geometry. This approach is significant for translating theoretical neuroscientific hypotheses into quantifiable metrics, particularly focusing on the neural representation of manifold structures.

Methodology

The paper combines topological data analysis (TDA) with variational autoencoders (VAEs) to explore the geometry of neural manifolds. The authors propose a method that:

1. Topology Learning: Establishes the topology of neural manifolds using TDA, identifying common structures such as rings, spheres, and tori (Figure 1).

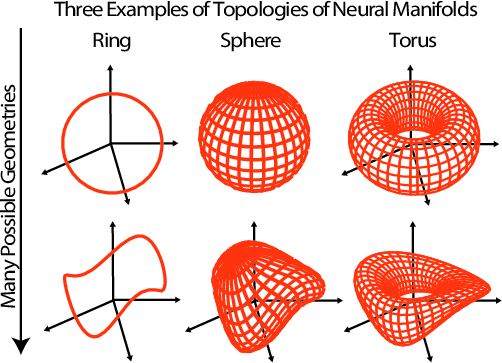
   Figure 1: Topology versus geometry. Topological methods reveal whether the neural manifold is a ring, a sphere, or a torus, i.e., whether it belongs to one of the three columns. Our geometric analysis determines the curvature of the ring, sphere, or torus—hence revealing their neural shape.

2. Deformation Learning: Utilizes a VAEs-based neural network to determine mappings that represent smooth deformations of known topologies. This mapping is critical for projecting the learned topological structures into neural state spaces (Figure 2).

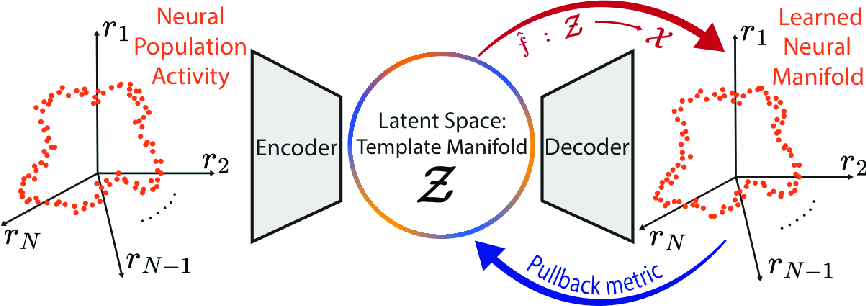
   Figure 2: Methods Overview. Neural activity vectors are represented as orange points in $\mathcal{X}$.

3. Geometry Learning: Applies differential geometric techniques to compute extrinsic curvature through the Riemannian pullback metric, providing a detailed analysis of the curvature profile of neural manifolds (Figure 3).

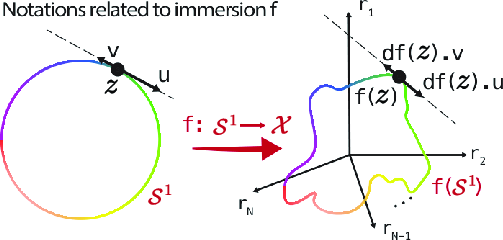
   Figure 3: Immersion $f$ sending $\mathcal{Z}$ into the neural manifold.

The method reliably estimates neural shape while being invariant to permutations of neuron order, ensuring robust application across various neural datasets.

Experiments with Synthetic and Real Neuroscientific Data

The paper tests the methodology on synthetic and real neural datasets, assessing performance through curvature estimation errors and geometric analysis.

Synthetic Data

For synthetic manifolds, experiments demonstrate precise topological learning and effective geometric reconstruction even under realistic noise conditions. The findings consistently showed minimal curvature estimation errors, which validated the approach (Figure 4).

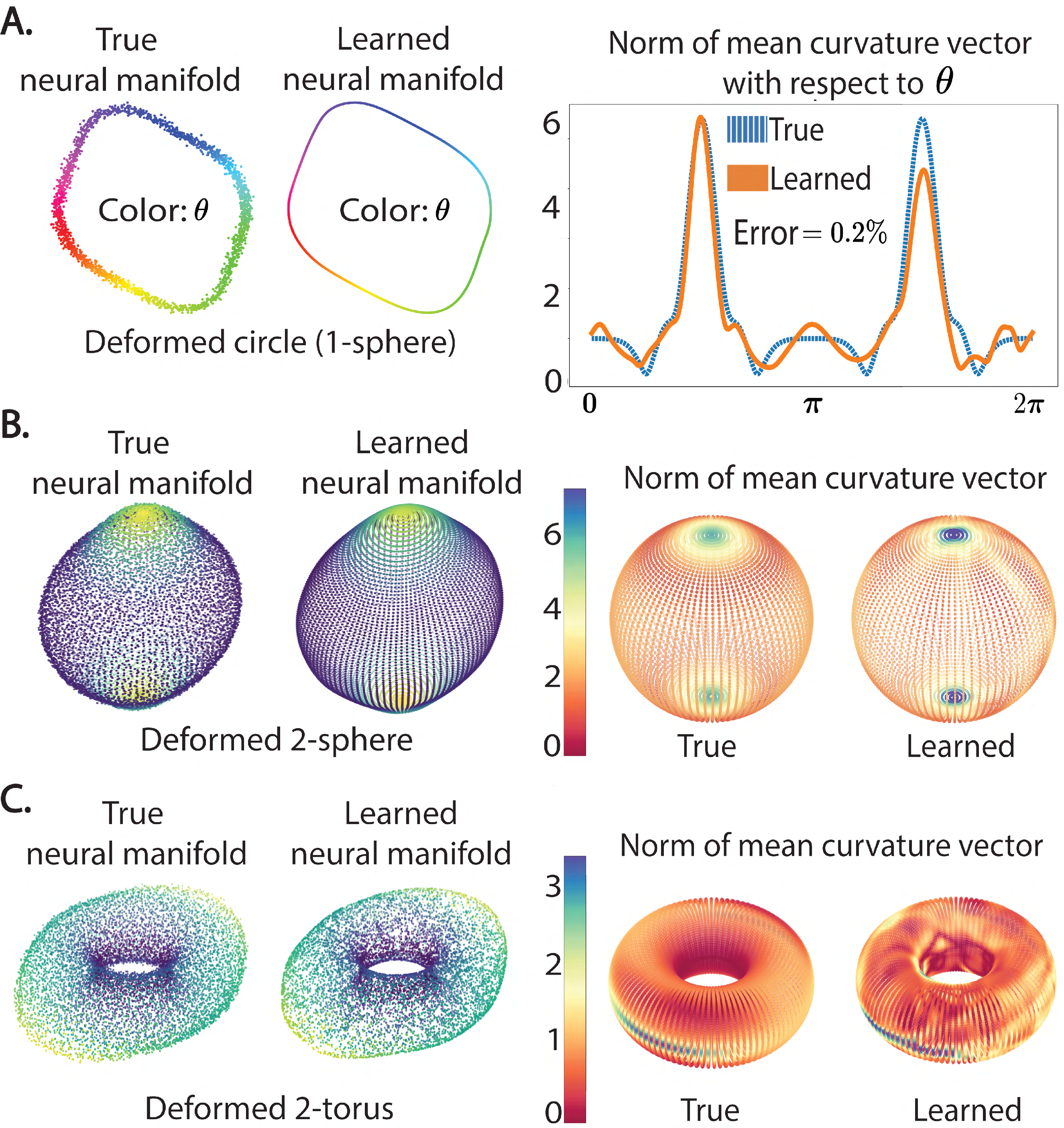
Figure 4: Synthetic manifolds created from smooth deformations of template manifolds $\mathcal{S}^1$, $\mathcal{S}^2$, and $\mathcal{T}^2$.

Simulated and Experimental Place Cells

Testing on simulated place cells illustrated the model's ability to reconstruct known geometric structures, confirming the recovery of established neural geometry patterns (Figure 5).

Figure 5: Simulated place cells. (A) Left: Simulated and reconstructed neural activity with respect to the positional angles of the animal in lab space.

Similarly, applying the approach to experimental data from rat hippocampal recordings revealed meaningful geometric insights consistent with prior knowledge of the spatial encoding by place cells (Figure 6).

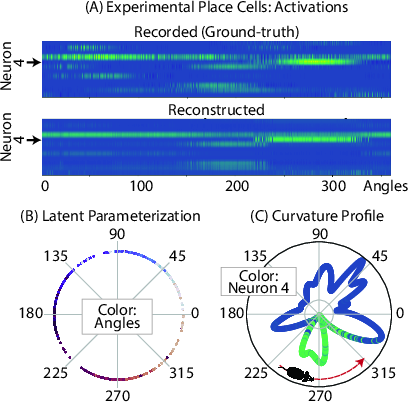
Figure 6: Experimental Place Cells. (A) Recorded versus reconstructed neural activity with respect to the animal's positional angles in lab space.

Theoretical and Practical Implications

This research posits substantial implications for neuroscience and artificial intelligence by providing a framework to quantify neural representations' geometric properties. It opens paths to exploring how neural circuits encode complex spatial and cognitive maps. The presented methods also encourage future research in extending the geometric understanding to more complex or abstract neural data structures. Additionally, understanding these manifolds has potential applications in improving the design of neural network architectures by drawing parallels between biological and artificial representations.

Conclusion

The paper effectively establishes a foundational approach to quantifying and understanding the geometric structures of neural manifolds. By bridging differential geometry with topological constraints, the methodology provides valuable insights into neural coding, revealing how abstract neural computations might translate into physical behaviors. Further work on integrating these quantitative measures with cognitive neuroscience theories could continue to enrich our understanding of the brain's manifold representation of the world.